Тема 12 Нормальное распределения вероятностей случайных величин

Нормальное распределение (N(а; ), закон Гаусса) с параметрами а и  имеет непрерывная случайная величина Х, если ее плотность распределения вычисляется по формуле

f(х) = .

Функция распределения: F(х) = .

Математическое ожидание и дисперсия: МХ = а, DХ = ^2..

На рисунках 23 и 24 изображены графики функций f(х) и F(х).

Рис. 23 Рис. 24

Функция Лапласа Ф₀(t) (см. приложение В) позволяет записать функцию нормального распределения в виде .

Вероятность попадания случайной величины X, распределенной по нормальному закону N(а; ), в интервал (х₁; х₂] вычисляется по формуле

Р(х₁ < Х  х₂) = .

Для нормально распределенной случайной величины верна формула

.

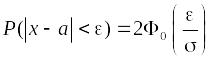Правило «трех сигм». Для нормально распределенной случайной величины Х практически достоверно, что все ее значения попадают в интервал (а – 3; а + 3).

Для распределений близких к нормальному используются также числовые характеристики: асимметрия и эксцесс . Они сравнивают «скошенность» (рис. 25) и «островершинность» (рис. 26) графиков плотности изучаемого и нормального распределений. Для нормального закона распределения, график плотности которого изображен на рисунках сплошной линией, асимметрия и эксцесс равны нулю.

Рис. 25 Рис. 26

_{Пример.} Случайная величина Х распределена по нормальному закону N(30; 10) Найти вероятность того, что случайная величина примет значение, принадлежащее интервалу (10; 50).

P(10 < X <50) = F(50) – F(10) =   =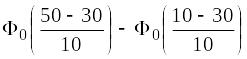

= Ф₀(2) – Ф₀(–2) = 2Ф₀(2).

Таблица приложения В: Ф₀(2) = 0,4772.

P(10 < X <50) = 20,4772  0,95.

Пример. Случайная величина Х распределена по нормальному закону N(а; ) Найти вероятность того, что случайная величина примет значение, принадлежащее интервалу (а – 3; а + 3).

P(а – 3 < X < а + 3) =   

Таблица приложения В: Ф₀(3) = 0,49865.

P(а – 3 < X < а + 3)  = 20,49865 = 0,9973.

Пример. Доказать, что функция распределения нормального закона

F(х) =  и функция Лапласа

связаны между собой формулой .

Тема 13 Связь между случайными величинами

Характеристикой связи между случайными величинами Х и Y является коэффициент корреляции

r_xy = М((Х – МХ)(Y – МY)).

1) Коэффициент корреляции удовлетворяет неравенству: .

2) Если случайные величины независимы, то r_xy = 0 (обратное утверждение неверно).

3)  тогда и только тогда, когда величины Х и Y связаны между собой линейной зависимостью.

При r_xy < 0,3 зависимость между величинами Х и Y считается слабой, при r_xy > 0,7 зависимость принимается сильной. Если Х и Y – зависимые величины, то приближенное представление Y в виде линейной функции от Х определяется уравнением линейной регрессии:

Y = МY + r_ху (Х – МХ).

Величина  = r_ху называется коэффициентом регрессии Y на Х.

Пример. Выбрать из чисел −3; 0,6; −0,6; 2 возможное значение коэффициента корреляции r_хy, если уравнение регрессии имеет вид: у = 2х − 3.

Знак r_хy совпадает со знаком коэффициента регрессии (коэффициента

при х) и следовательно, r_хy = 0,6.

Пример. Совместное распределение дискретных случайных величин Х, Y задано таблицей, содержащей вероятности p_ij событий

{Х = х_i; Y = у_j}.

Y Х	0	2	4	pi
2	0,1	0,2	0,25	0,55
–2	0,2	0,15	0,1	0,45
pj	0,3	0,35	0,35

Записать уравнение регрессии.

МY = 00,3 + 20,35 + 40,35 = 2,1;

М(Y ²) = 0²0,3 + 2²0,35 + 4²0,35 = 7.

DY = М(Y ²) – (МY) ² = 7 – 2,1² = 2,59;

МX= 20,55 – 20,45 = 0,2;

М(X ²) = 2²0,55 + 2²0,45 = 4.

DX = М(X ²) – (МX) ² = 4 – 0,2² = 3,96;

М(ХY) = 020,1+0(–2)0,2+220,2+2(–2)0,15+420,25+2(–2)0,1 = 1,4.

М((Х – МХ)(Y – МY)) = М(ХY – ХМY – YМХ + МХМY) =

=М(ХY) – МYМХ = = 1,4 – 2,10,2 = 0,98.

Коэффициент корреляции: М((Х–МХ)(Y–МY)) =

Существует умеренная зависимость между случайными величинами Х, Y.

Уравнение линейной регрессии: Y = МY + r_ху (Х – МХ) = 0,24х + 2,05.

Пример. Доказать, что модуль коэффициента корреляции r_xy  равен единице, если случайные величины Х, Y связаны линейной зависимостью.

Y = Х + ; МY = МХ + , DY = ²DХ, _y = _х.

r_xy = М((Х–МХ)(Y–МY)) = М((Х–МХ)(Х +  – МХ – )) =

= М(Х – МХ)² =