Тема 8 Функция распределения и плотность вероятности

Случайной величиной Х называется переменная величина, принимающая в результате испытания одно из множества возможных значений.

Определение. Функция распределения F(х) случайной величины Х равна вероятности события {Х < x} для любого вещественного числа х:

F(х) = Р(Х < х).

Функция распределения полностью характеризует случайную величину. Случайная величина х называется дискретной, если множество ее значений конечно или счетно. Дискретная случайная величина задается законом распределения, т. е. множеством упорядоченных пар (x_i; p_i), где х_i – возможные значения случайной величины, p_i – вероятности принятия случайной величиной значений x_i, 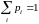(табл. 1).

Таблица 1

хi	х1	х2	х3	…	хn
рi	р1	р2	р3	…	рn

Функция распределения дискретной случайной величины определяется формулой

,

где суммируются вероятности значений x_i меньших x. График функции распределения представлен на рисунке 14

Рис. 14

Неслучайную величину С можно рассматривать как случайную с законом распределения

Таблица 2

хi	С
рi	1

Непрерывная случайная величина может принимать все значения из некоторого (конечного или бесконечного) промежутка. Если функция F(х) дифференцируема, то ее производная f(х) = F (х) называется плотностью распределения вероятностей. Плотность вероятности полностью характеризует непрерывную случайную величину.

Пример. Доказать, что при любых значениях х₁, х₂ (х₁ < х₂) вероятность события {х₁  Х < х₂} равна F(х₂) – F(х₁).

А = {Х < х₁}, В = {Х < х₂}, Р(А) = F(х₁), Р(В) = F(х₂).

С = {х₁  Х < х₂}, А  С = , В = А + С, Р(В) = Р(А) + Р(С) .

Р{х₁  Х < х₂} = Р(С) = Р(В) – Р(А) = F(х₂) – F(х₁).

Свойства функции распределения и плотности вероятности

1) Р(а  Х < b) = F(b) – F(a).

2) Для непрерывной случайной величины Р(а  Х < b) =  . Вероятность попадания случайной величины Х в интервал [a; b) равна площади криволинейной трапеции abBA (рис. 15).

3) Для непрерывной случайной величины Р(х = а) = Р(х = b) = 0, следовательно, Р(а  Х < b) = Р(а < Х < b) = Р(а  Х  b) = Р(а < Х  b).

4) .

5) неубывающая функция.

6) .

7) f(х)  0.

8) f(х) = F (х) и F(х) = .

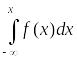9) 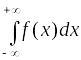  = 1. Площадь S, заключенная между графиком плотности распределения f(х) и осью 0х, равна единице (рис. 15).

Рис. 15

Пример. Для дискретной случайной величины

xi 0 1 2 3 pi 0,1 0,4 0,2 0,3

построить график функции распределения F(x), вычислить .

.

Функция распределения F(x):

если , то событие {Х < 0} невозможно и F(x) = P(Х < 0) = 0;

если , то F(x) = P(Х < 1) = P(Х = 0) = 0,1;

если , то F(x) = P(Х < 2) = P(Х = 0) + P(Х = 1) = 0,1 + 0,4 = 0,5;

если , то F(x) = P(Х < 3) = 0,1 + 0,4 + 0,2 = 0,7;

в случае х(3;) случайная величина принимает все значения из таблицы, т.е. событие становится достоверным и F(x) = 1.

Функция распределения F(x) и ее график:

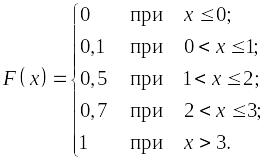
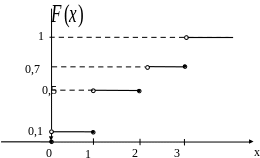
Рис. 16

Пример. По мишени производится 3 независимых выстрела с вероятностью попадания при каждом выстреле . Найти закон распределения случайной величины Х, равной числу попаданий в мишень.

Возможные значения случайной величины Х: 0; 1; 2; 3.

По формуле Бернулли при n = 3; р = 0,8; q = 0 ;2 : , ,

, .

Закон распределения:

xi pi 0,008 0,096 0,384 0,512

Проверка 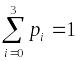: 0,008 + 0,038 + 0,384 + 0,512 =1.

Пример. Функция распределения случайной величины Х имеет вид:

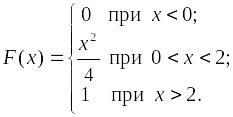Найти вероятность того, что случайная величина примет значение из интервала [1; 1,5), и определить плотность распределения f(х).

Р(1  х < 1,5) = F(1,5) – F(1) = .

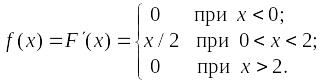
Пример. Установить при каком значении параметра A функция является плотностью вероятности некоторой случайной величины Х ( > 0). Найти функцию распределения F(x) случайной величины Х. Вычислить вероятность попадания случайной величины Х в промежуток [0; 1].

Функция распределения:

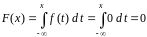при х  0;

при х > 0.