Интервальные оценки параметров

Интервальной оценкой оцениваемого параметра  генеральной совокупности называется интервал (^* – ; ^* + ), накрывающий истинное значение  параметра с заданной вероятностью , которая называется доверительной вероятностью P(^*–  <  < ^*+ ) = . Интервал (^* – ; ^* + ) называется доверительным интервалом (рис. 5),  – точностью оценки.

Рис. 5

Если при построении интервальных оценок математического ожидания и среднего квадратического отклонения предполагается, что генеральная совокупность Х распределена по нормальному закону с параметрами a и , то доверительные интервалы находятся по формулам 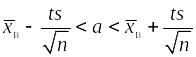и 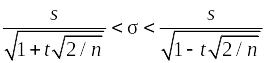. Значения t, удовлетворяющие уравнению , приведены в приложении В.

При увеличении объема выборки n доверительный интервал уменьшается. Увеличение доверительной вероятности  ведет к росту значения t (см. приложение В), т.е. увеличению доверительного интервала.

Пример. Точечная оценка параметра распределения равна 20. Установить, какой из интервалов (20; 21), (19; 21), (0, 20), (19, 20) может служить интервальной оценкой?

Интервальной оценкой (^* – , ^* + ) является интервал (19; 21) при ^* = 20 и  = 1.

Пример. Дан группированный статистический ряд:

Интер- вал	[30; 40]	(40; 50]	(50; 60]	(60; 70]	(70; 80]	(80; 90]	(90; 100]	(100; 110]
	2	6	14	26	28	15	7	2

Построить доверительные интервалы для математического ожидания при доверительной вероятности ₁ = 0,9 и среднего квадратического отклонения при доверительной вероятности ₂ = 0,95.

Дополнительная таблица:

Интервал		Середина интервала
[30; 40]	2	35	70	2450
(40; 50]	6	45	270	12150
(50; 60]	14	55	770	42350
(60; 70]	26	65	1690	109850
(70; 80]	28	75	2100	157500
(80; 90]	15	85	1275	108375
(90; 100]	7	95	665	63175
(100; 110]	2	105	210	22050

Выборочное среднее:

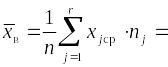
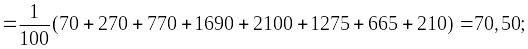выборочная дисперсия:

выборочное среднее квадратическое отклонение ;

исправленное среднее квадратическое отклонение:

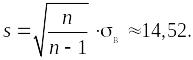
Точечные оценки параметров генеральной совокупности: математическое ожидание а = 70,50 и среднее квадратическое отклонение

Доверительная вероятность для а: ₁ = 0,9.

Таблица значений функции Лапласа (приложение В):

2 (1,65)  0,9.

Замечание. Число 0,4505, ближайшее к , расположено в строке «1,6» и столбце «5». Искомое значение t =1,6 + 0,05 = 1,65.

Доверительный интервал для математического ожидания a:

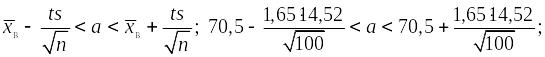
68,1 < a < 72,9 с надежностью 0,9.

Доверительная вероятность для : ₂ = 0,95.

Таблица значений функции Лапласа (приложение В): .

t = 1,96 при надежности ₂ = 0,95.

Доверительный интервал для среднего квадратического отклонения:

;

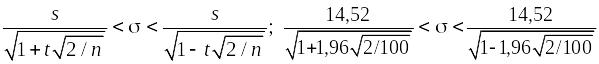12,85 <  < 17.08 с надежностью 0,95.