Тема 14 математическая статистика Основные задачи математической статистики

Математическая статистика – раздел математики, в котором изучаются методы обработки и анализа результатов наблюдений массовых случайных явлений. Генеральной совокупностью Х называется множество изучаемых объектов, а также результаты наблюдений, характеризующие какое-нибудь свойство объекта. Выборкой называется случайно отобранный набор объектов множества Х или результаты наблюдений. Генеральную совокупность можно считать случайной величиной Х, а выборку – последовательностью случайных величин Х₁, Х₂,  … Х_n, каждая из которых имеет такое же распределение, как и генеральная совокупность. Число отобранных объектов n (или проведенных опытов) называется объемом выборки.

Основные задачи математической статистики:

1) оценка по выборке характеристик генеральной совокупности, точности и надежности оценок;

2) прогнозирование состава новых выборок из той же генеральной совокупности.

Статистическое распределение выборки

Пусть в результате испытаний получен набор значений , причем каждое значение было зафиксировано раз; . Значения x_i называются вариантами, последовательность вариант, записанных в возрастающем порядке, – вариационным рядом. Числа n_i называются частотами, их отношения к объему выборки – относительными частотами.

Статистическим распределением выборки (статистическим рядом) называется перечень вариант и соответствующих им частот, который обычно оформляется в виде таблиц 1 или 2.

Таблица 1 Таблица 2

xi	x1	x2		xk		xi	x1	x2		xk
ni	n1	n2		nk		wi	n1/n	n2/n		nk/n

Сумма всех чисел второй строки таблицы 2 равна единице: . Графическое представление статистического ряда в виде ломаной линии (рис. 1) называется полигоном частот.

Рис. 1

При большом количестве столбцов в таблице 1 составляется группированный статистический ряд (таблица 3), где и минимальное и максимальное значения элементов выборки. Диапазон значений выборки точками разбивается на r непересекающихся промежутков длины . Затем для каждого промежутка подсчитываются частоты – количество вариант, попавших в данный интервал. Значение варианты для каждого промежутка принимается равным середине промежутка.

Таблица 3

Интервал
ni	n1	n2		nr

Эмпирическая функция распределения. Гистограмма

Эмпирической функцией распределения называется функция где n_х – число членов вариационного ряда, меньших х.

Функция равна относительной частоте события {х_i < х} и обладает следующими свойствами:

1) если x₁ – наименьшая варианта, то при ,

2) если x_k – наибольшая варианта, то при ;

3) – неубывающая функция;

4) .

При большом количестве промежутков со значительным числом вариант в каждом из них , т.е. ломаная , давая представление о гладкой кривой , служит оценкой теоретической функции распределения генеральной совокупности.

Теорема. Для любого положительного числа  при любом значении х вероятность события стремится к единице при n.

Это означает, что функция сходится по вероятности к теоретической функции распределения генеральной совокупности . Для построения F^*(x) исходный вариационный ряд (таблица 1) дополняется двумя строками: накоплений частот ( ) и относительных частот .

Таблица 4

xi	x1	x2		xk
ni	n1	n2		nk
Ni	N1 = n1	N2 = N1 + n2		Nk = Nk –1 + nk = n
Ni /n	N1 /n	N2 /n		Nk /n = 1

Данные, приведенные в таблице 4, дают возможность задать все значения функции :

График подобной функции при k = 5 представлен на рисунке 2.

Рис. 2

Для непрерывной теоретической функции распределения график строится приближенно по точкам , которые соединяются отрезками, как это показано на рисунке 3.

х₂

х₅

Рис. 3

Аналогом графика плотности распределения случайной величины в математической статистике является гистограмма. Построенная таблица группированного ряда дополняется тремя строками (таблица 5): длина интервала , относительная частота , плотность относительной частоты .

Таблица 5

Интервал
ni	n1	n2		nk
hi	h1	h2		hk
wi	n1/n	n2/n		nk/n
wi / hi	w1/ h1	w2/ h2		wk/ hk

Гистограмма представляет собой набор прямоугольников высоты (возможно также ) и основанием [x_j–1; x_j] (рис 4).

Рис. 4

Площадь каждого прямоугольника совпадает с соответствующей относительной частотой w_j (или частотой n_j при высотах ). Общая площадь, ограниченная гистограммой, равна единице (или объему выборки n). После сглаживания гистограмма – аналог плотности распределения непрерывной случайной величины.

Пример. Из генеральной совокупности извлечена выборка объёмом n = 50.

xi [0; 1] [1; 2) [2; 3) (3; 4] ni 10 9 8 n4

Результаты наблюдений сведены в таблицу. Найти значение n₄.

Объем выборки: 10 + 9 + 8 + n₄ = 50; n₄ = 23.

Пример. По выборке объёма n = 100 построена гистограмма.

Найти значение а.

Высоты гистограммы: .

Площадь гистограммы S равна объему выборки.

Основания прямоугольников: h = 2.

S = 4  2 + 12  2 + 18  2 + а  2 = 100; а = 16.

Пример. Случайная величина задана группированным рядом.

	Интервал	(0; 1]	(1; 2]	(2; 3]	(3; 4]
		10	9	8	23

Построить график эмпирической функцией распределения.

Таблица дополняется двумя строками: и .

	Интервал	(0; 1]	(1; 2]	(2; 3]	(3; 4]
		10	9	8	23
		10	19	27	50
		0,2	0,38	0,54	1

Аналитическое представление эмпирической функции распределения:

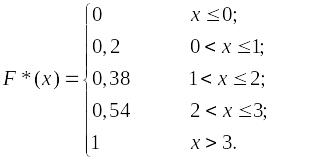
График F*(х) – это отрезки прямых F*(х) = 0,2; F*(х) = 0,38; F*(х) = 0,54 на интервалах (0; 1]; (1; 2]; (2; 3], дополненных линиями F*(х) = 0 при x  0 и F*(х) =1 при x > 3.

2