Graf3
.docxПетербургский государственный университет путей сообщения
Императора Александра I
Кафедра «Математика и моделирование»
Расчётно-графическая работа №2
«Построение минимального остова для неориентированной сети»
Выполнил студент Д, А, Баранов
Факультет: АИТ
Группа: АР-709
Номер зачётной книжки: 01-709-02
Проверил: Ю.В. Боровских
Санкт-Петербург
2018
Задача.
Представить графически неориентированную
сеть
,
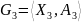заданную весовой матрицей
.
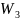Построить минимальный остов для сети
с помощью алгоритма Краскала.
Весовая матрица:
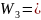
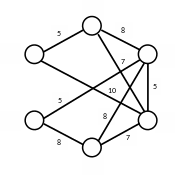
13
Рис. 1 – заданный остов
Решение.
Шаг 1. Сортируем рёбра сети по их весам.
[
];
[
];
[
];
[
];
[
];
[
];
[
];
[
];
[
];
[
].
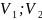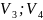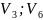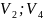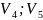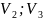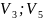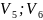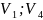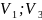1-ая итерация.
Шаг
2.
Каждую вершину сети помещаем в отдельную
ячейку
.
,
,
,
,
,
.
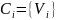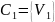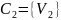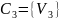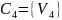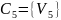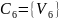Число вершин n=6.
Шаг 3. Полагаем E`=Ø.
Шаг 4. Удаляем первое ребро из данной последовательности рёбер.
e=[ ].
Шаг 5. Проверяем, не входят ли уже заданные точки.
.
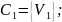
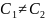Значит, объединяем ячейки E`=
E` ⋃
{e} = {[
]}.
=
⋃
= {
}.
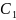Шаг 6. Проверяем условие на завершение алгоритма.
#E`= m-1. Условие не верно, т.к. #E`=1, а m-1 = 5.
Переходим к следующей итерации.
2-ая итерация.
Шаг 4. Удаляем следующее ребро из данной последовательности рёбер.
e=[ ].
Шаг 5. Проверяем, не входят ли уже заданные точки.
.
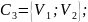
Значит, объединяем ячейки E`=
E` ⋃
{e} = {[
]}.
=
⋃
= {
}.
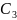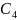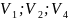Шаг 6. Проверяем условие на завершение алгоритма.
#E`= m-1. Условие не верно, т.к. #E`=2, а m-1 = 5.
Переходим к следующей итерации.
3-ая итерация.
Шаг 4. Удаляем следующее ребро из данной последовательности рёбер.
e=[ ].
Шаг 5. Проверяем, не входят ли уже заданные точки.
.
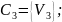
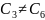Значит, объединяем ячейки E`=
E` ⋃
{e} = {[
]}.
=
⋃
= {
}.
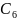Шаг 6. Проверяем условие на завершение алгоритма.
#E`= m-1. Условие не верно, т.к. #E`=3, а m-1 = 5.
Переходим к следующей итерации.
4-ая итерация.
Шаг 4. Удаляем следующее ребро из данной последовательности рёбер.
e=[ ].
Шаг 5. Проверяем, не входят ли уже заданные точки.
=
{
}.
.
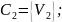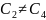Значит, объединяем ячейки E`=
E` ⋃
{e} = {[
]}.
=
⋃
= {
}.
Шаг 6. Проверяем условие на завершение алгоритма.
#E`= m-1. Условие не верно, т.к. #E`=4, а m-1 = 5.
Переходим к следующей итерации.
5-ая итерация.
Шаг 4. Удаляем следующее ребро из данной последовательности рёбер.
e=[ ].
Шаг 5. Проверяем, не входят ли уже заданные точки.
.
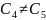Значит, объединяем ячейки E`=
E` ⋃
{e} = {[
]}.
=
⋃
= {
}.
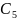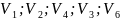Шаг 6. Проверяем условие на завершение алгоритма.
#E`= m-1. Условие верно, т.к. #E`=5, а m-1 = 5.
Переходим к следующей итерации.
6-ая итерация.
Шаг 4. Удаляем следующее ребро из данной последовательности рёбер.
e=[ ].
Шаг 5. Проверяем, не входят ли уже заданные точки.
.
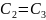Входят,
поэтому переходим к следующей итерации.
7-ая итерация.
Шаг 4. Удаляем следующее ребро из данной последовательности рёбер.
e=[ ].
Шаг 5. Проверяем, не входят ли уже заданные точки.
.
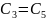Входят, поэтому переходим к следующей
итерации.
8-ая итерация.
Шаг 4. Удаляем следующее ребро из данной последовательности рёбер.
e=[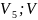
6].
Шаг 5. Проверяем, не входят ли уже заданные точки.
.
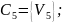
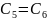Входит, поэтому завершаем итерации.
Шаг 6. Проверяем условие на завершение алгоритма.
#E`= m-1. Условие верно, т.к. #E`=5 и m-1 = 5.
Остов минимального веса равен: M=5+7+5+5+7=29.
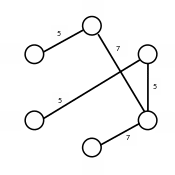
Рис. 2 –остов минимального веса