Лабораторные работы / 9283_Зикратова_1_лаб

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В. И. Ульянова (Ленина)

Кафедра ФЭТ

отчёт

по лабораторной работе №1

по дисциплине «Электродинамика»

Тема: ИССЛЕДОВАНИЕ ДИСПЕРСИИ ВОЛН В ВОЛНОВОДЕ И В КОАКСИАЛЬНОЙ ЛИНИИ ПЕРЕДАЧИ

Студенты гр. 9283		Брацышко К. Б.
		Зикратова А. А.
		Смирнова О. А.
		Шипков В. Е.
Преподаватель		Дроздовский А. В.

Санкт-Петербург

2021

Цель работы:

изучение свойств и конструкции коаксиальной линии и прямоугольного волновода, а также методики измерения длины волны в линии передачи и параметров, характеризующих режим ее работы.

Основные теоретические положения

СВЧ-линией передачи называется устройство, ограничивающее область распространения электромагнитных волн СВЧ-диапазона и позволяющее передавать поток их электромагнитной энергии в заданном направлении.

В общем случае в линиях передачи, исследуемых в данной работе, может существовать бесконечное множество волн типа E_mn и H_mn (волны дисперсионного типа), отличающихся индексами m и n, которые определяют количество полуволн, укладывающихся внутри поперечного сечения линии передачи.

Критическая длина (λ_кр) волны является основным параметром, определяющим возможность существования определенного типа волн в линии передачи на заданной частоте. Условием распространения электромагнитной волны в волноводе с рабочей частотой: λ < λ_кр, где λ – длина волны в данной неограниченной среде. Длина волны в волноводе:

Блок-схема лабораторной установки приведена на рис. 1. Измерительная линия представляет собою отрезок волновода с продольной щелью в середине широкой стенки.

Рис. 1

Протокол

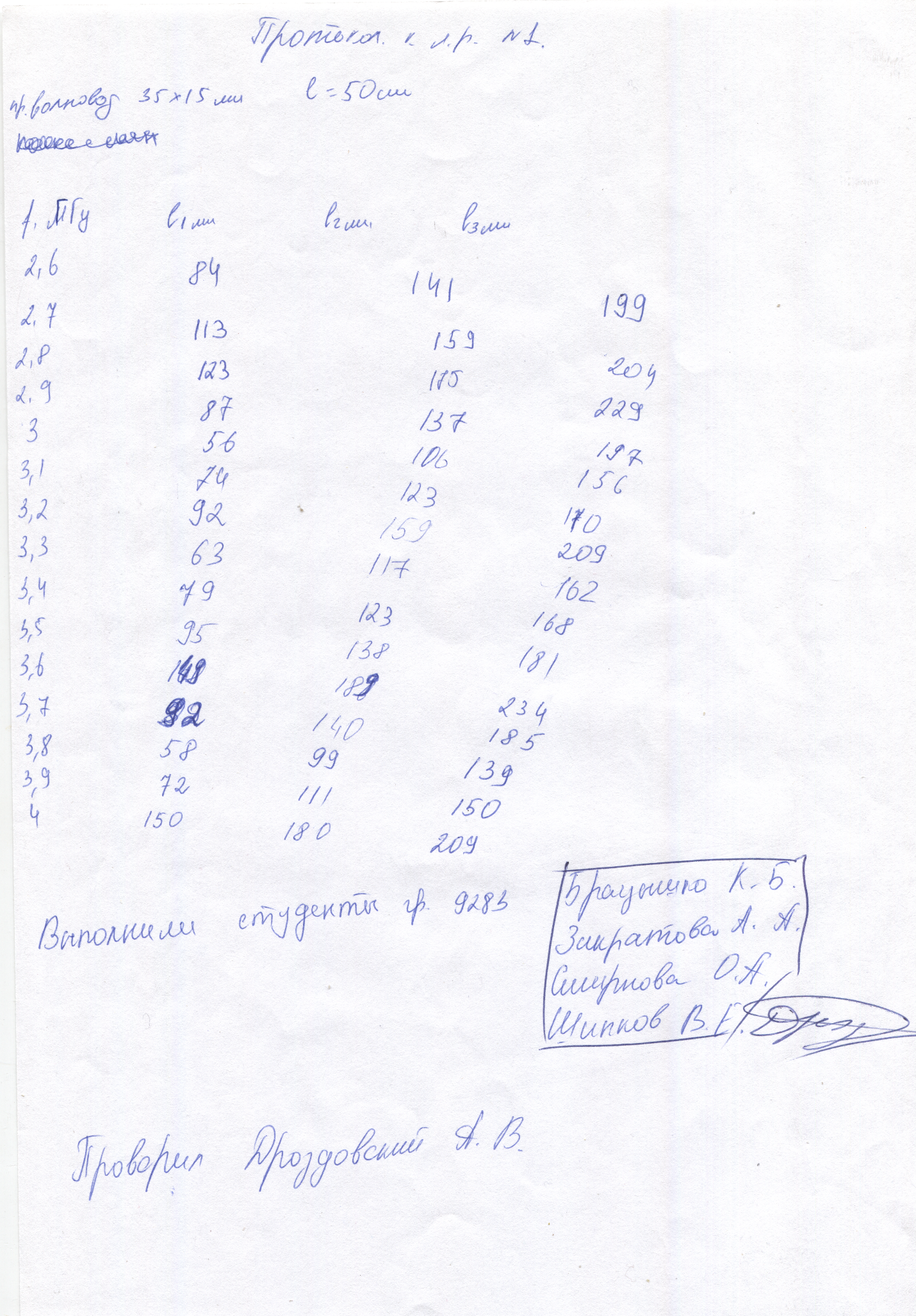
Обработка результатов

1. Коаксиальная линия:

Пример расчёта для f = 3,4 ГГц:

λ₁ = (l₂ – l₁) ‧ 2/1000 = (123 – 79) ‧ 2/1000 = 0,088 м,

λ₂ = (l₃ – l₂) ‧ 2/1000 = (168 – 123) ‧ 2/1000 = 0,09 м,

λ_в = (λ₁ + λ₂)/2 = (0,088 + 0,09)/2 = 0,089 м, k_в = = = 70,6 м^-1

= ≈ 0,88 м, k = = ≈ 71,26 м^-1

Рис. 1 – Экспериментальная и теоретическая зависимости длины волны от частоты

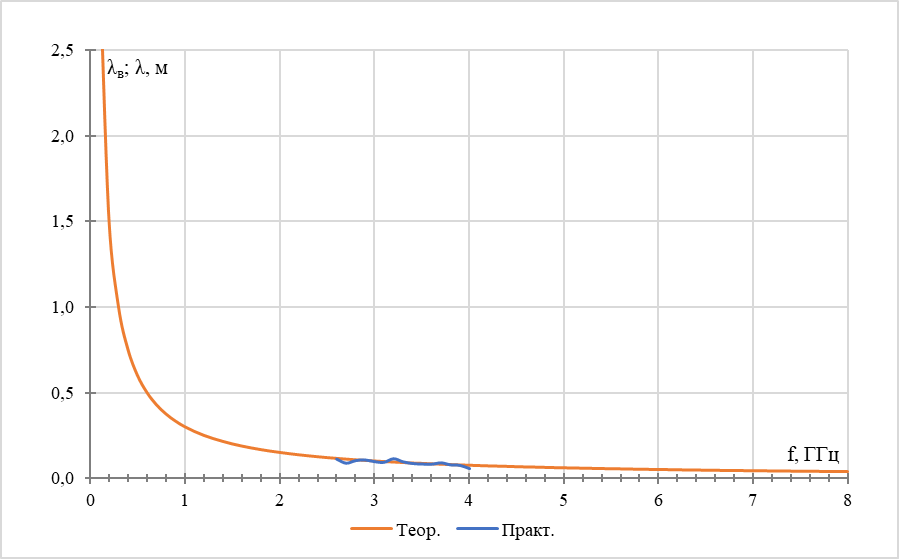
Рис. 2 – Экспериментальная и теоретическая зависимости частоты от волновых чисел

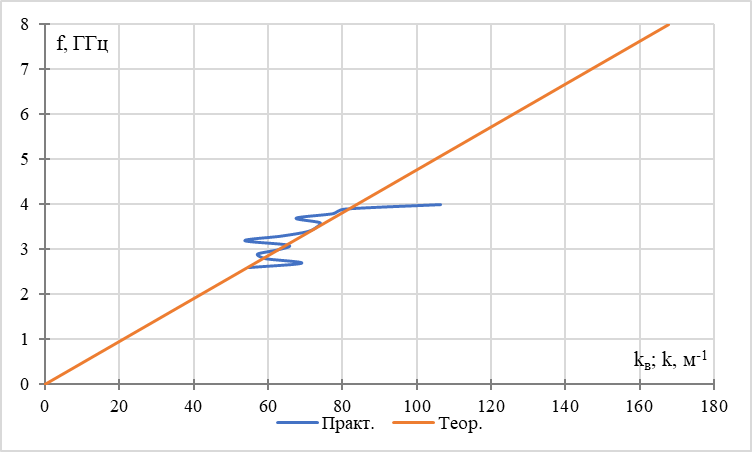
Рис. 3 – Фазочастотная характеристика коаксиальной линии

k_в = , → , где l = 0,5 м – длина измерительной линии

, k =

Рис. 4 – Законы дисперсии, полученные из фазочастотной характеристики и по формулам, приведённым выше (коаксиальная линия)

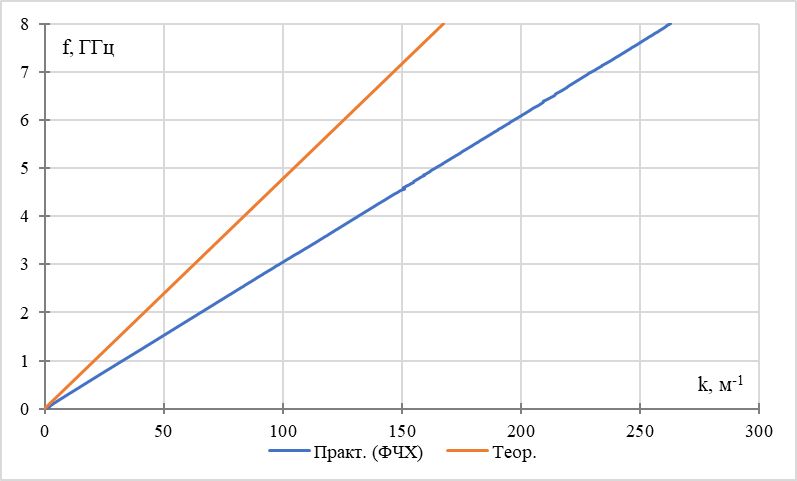
Рис. 5 – Закон дисперсии, полученный из фазочастотной характеристики коаксиальной линии

2. Прямоугольный волновод:

Частота отсечки, установленная экспериментально: f_{отсеч.(эксп)} ≈ 4,17 ГГц

Рис. 5 – Передаточная характеристика прямоугольного волновода

f_{отсеч.(эксп)} ≈ 4,17 ГГц

Частота отсечки, установленная теоретически:

a = 0,035 м, b = 0,015 м – размеры волновода, H₁₀ – основная мода волновода

,

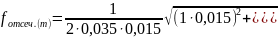≈ 4,28 ГГц

Рис. 6 – Фазочастотная характеристика прямоугольного волновода

≈ -660

≈ 4,37 ГГц

β_(э) = , → , где l = 0,5 м – длина измерительной линии, ∆φ – фаза в [рад]

Пример расчёта для f = 4,37 ГГц:

= ≈ 0,273 м; ≈ -23, можно взять ≈ 23

Рис. 7 – Зависимость , полученная из фазочастотной характеристики прямоугольного волновода

Пример расчёта для f = 4,37 ГГц:

λ_в(т) = = ≈ 0,342 м

β_(т) = = ≈ 18,35 м^-1

Рис. 8 – Зависимость 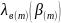, полученная по формулам, приведённым выше

Рис. 9 – Законы дисперсии, полученные из фазочастотной характеристики и по формулам (прямоугольный волновод)

Вывод: в ходе лабораторной работы были получены законы дисперсии для прямоугольного волновода (основная мода H₁₀) и коаксиальной линии (T – волна), изучена методика измерения длины волны в передаточной линии (создавали стоячую волну в линии, фиксировали положения минимумов или максимумов амплитуды поля, высчитывали λ_в). В коаксиальной линии для T- волны закон дисперсии имеет линейный вид, что подтвердилось экспериментально. Для прямоугольного определили частоту отсечки 2-мя способами: через коэффициент передачи и расчёт по формуле для основной моды.