
ИПР 1Тpdf
.pdfМинистерство образования Республики Беларусь Учреждение образования
«Белорусский Государственный университет информатики и радиоэлектроники»
Индивидуальная практическая работа№1 по дисциплине
Теория вероятностей и математическая статистика
Выполнил:Назаров .Н Группа 910901
2021
Задача № 1 (33)
В урне 6 белых и 7 черных шаров. Из урны вынимают шар – отмечается его цвет и он возвращается в урну, после этого вынимают второй шар. Найти вероятность, что шары будут одинакового цвета.
Решение.
Вероятность Р(А1) первый и второй разы вытащить из урны белый шар равна 136 136 , вероятность Р(А2) первый и второй разы вытащить из урны чёрный
шар равна 137 137 .
Тогда искомая вероятность равна:
P( A)
Ответ:
6 |
|
6 |
|
7 |
|
7 |
|
36 49 |
0, 503 |
13 |
|
|
|
|
|||||
|
13 |
|
13 13 |
|
169 |
|
|||
P( A) 0, 503 |
|
|
|
||||||
Задача № 2 (33)
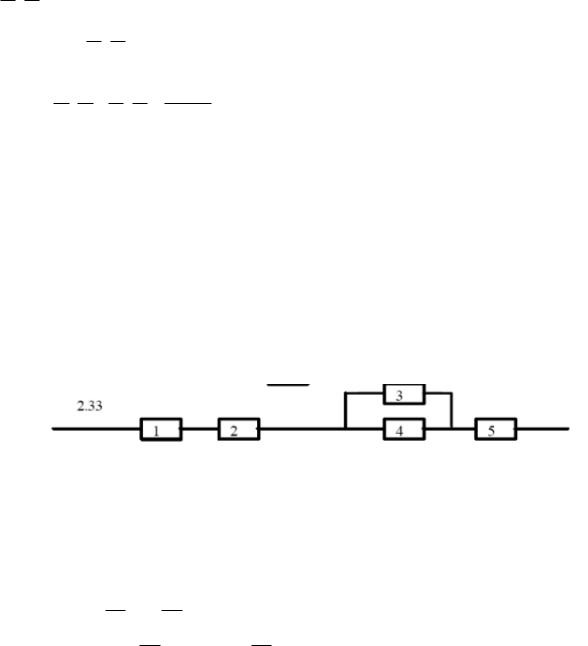
Приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны q1=0,1; q2=0,2; q3=0,3; q4=0,4; q5=0,5 q6=0,6 . Найти вероятность того, что сигнал пройдет со входа на выход.
Решение.
Пусть событие АI состоит в том, что сигнал безотказно пройдёт по участку цепи 3-4 с параллельным соединением, событие АII состоит в том, что сигнал безотказно пройдёт по участку цепи 1-2- АI -5 с последовательным соединением.
P( A ) 1 P( A ) |
|||
I |
3 |
||
|
|
|
|
|
|
|
|
P( AII |
) P( A ) P( |
||
|
1 |
||
Ответ: р=0,3168
P(
A2
A |
) 1 q |
q |
1 0,12 |
4 |
3 |
4 |
|
|
|
) P( АI ) P( A5) 0,9 0,8
0,88
0,88 0,5 0,3168

Задача № 3 (33)
На наблюдательный пункт станции установлены четыре радиолокатора различных конструкций. Вероятность обнаружения цели с помощью первого локатора равна 0,7, второго - 0,8 , третьего - 0,9 , четвертого - 0,93.
Наблюдатель включает один локатор. Найти вероятность обнаружения цели.
Решение.
Рассмотрим событие А – цель обнаружена. С ним связаны гипотезы: А1 - включен первый локатор, А2 - включен второй локатор, А3 - включен третий локатор,
А4 - включен четвёртый локатор.
P H |
P H |
P H |
P H |
|
1 |
|
|||||
1 |
2 |
3 |
4 |
|
4 |
|
|
|
|
|
Условная вероятность:
P P P P
A / H A / H A / H A / H
1 2 3 4
0, 7;
0,8;
0, 9;
0, 93.
По формуле полной вероятности:
P( A) P(H |
) P( A / H |
) P(H |
) P( A / H |
) P(H |
) P( A / H |
) P(H |
) P( A / H |
) |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
|
1 0, 7 0,8 0,9 0,93 0,8325 4
Ответ: Р=0,8325

Задача № 4 (33)
В результате многолетних наблюдений установлено, чтовероятность выпаения дождя 1 октября в данном городе равна 1/7.Определить наивероятнейшее число дождливых дней 1 октября в данном городе за 40 лет.
Решение.
Наивероятнейшее число
m0
наступлений события А при n опытах
определяется из неравенства:
n p q m0 n p p
Получим:
Ответ:
m0
40 |
1 |
|
6 |
m |
40 |
|
1 |
|
1 |
|
|
|
|
||||||
|
7 |
|
7 |
0 |
|
|
7 |
|
7 |
|
|
|
|
|
|
||||
4,857 m 5,857 |
|
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
|
m 5 |
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
5 .
