Конспекты лекций по Интеллектуальным системам / Л12 - Неинф поиск-1

Лекция 12.

Методы неинформированного поиска. Поиск в ширину, в глубину, однородной стоимости, ограниченный по глубине поиск.

Основная проблема в области поиска – нахождение хорошей стратегии поиска для заданной задачи.

Стратегии принято оценивать с помощью 4 критериев:

• Полнота – гарантированное нахождение решения, если оно существует;

• Временная сложность – время поиска решения конкретной задачи;

• Емкостная сложность – затраты памяти;

• Оптимальность – способность находить наилучшее решение (решение минимальной стоимости).

Стратегии поиска в пространства состояний принято делить на две группы:

1. Стратегии неинформированного (слепого) поиска.

2. Стратегии информированного поиска (эвристические cтратегии).

Неинформированный поиск – это поиск в отсутствии какой-либо информации, позволяющей отдавать предпочтение одним направлениям поиска перед другими.

Информированный поиск имеет место, когда есть некоторая информация, которая может использоваться при выборе того или иного направления поиска.

Стратегии неинформированного поиска

Поиск (сначала) в ширину.

Сначала раскрывается вершина – корень в дереве поиска. Затем все вершины – непосредственные потомки корня и т.д. Вершины глубины d раскрываются раньше, чем вершины глубины (d+1). Пока есть хотя бы одна вершина глубины d – нельзя раскрывать вершину на глубине d+1. Поиск в ширину может быть реализован алгоритмом General-Search, в котором функция построения очереди помещает вновь сгенерированные вершины в конец очереди.

function Breadth-First-Search(Problem) returns solution or failure

return General-Search(Problem, En-queue-At-End)

Cтратегия помещает вновь сгенерированные вершины в конец очереди.

Поиск в ширину:

– гарантирует нахождение решения, если оно существует;

– первым всегда находит решение минимальной глубины.

Однако решение минимальной глубины не всегда имеет минимальную стоимость.

Недостаток поиска в ширину – большая сложность.

Пусть пространство поиска, в котором каждое состояние может быть раскрыто в b новых состояний. Тогда корень дерева генерирует b потомков, далее b², затем b³ и так далее.

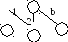
Следовательно, если решение лежит на глубине d, для нахождения решения потребуется раскрыть 1 + b + b² + b³ + … + b^d вершин.

Порядок сложности поиска – O(b^d).

Оценим временную и емкостную сложность поиска при коэффициенте ветвления b=10 и глубине равной d. Пусть за одну секунду проверяется 1000 вершин (раскрываются и проверяются на достижение цели).

d	Вершины	Время	Память
0	1	1 мс	100 байт
2	111	0,1 с	11 кбайт
4	11111	11 с	1 Мбайт
6	106	18 м	111 Мбайт
8	108	314 ч	11 Гбайт
10	1010	128 дн	1 Тбайт
12	1012	35 лет	111 Тбайт
14	1014	3500 лет	11111 Тбайт

Поиск по критерию стоимости.

Поиск в ширину всегда находит целевое состояние минимальной глубины в дереве поиска, однако ему не всегда соответствует решение минимальной стоимости.

Поиск по критерию стоимости – модифицированная стратегия поиска в ширину, при которой всегда раскрывается вершина с минимальной стоимостью пути. Пусть

g(n) – функция стоимости пути в вершину n.

Поиск в ширину является частным случаем поиска по критерию стоимости, когда стоимость равна глубине.

g(n) = depth(n).

Пример: Рассмотрим пути поиска в графе рис. 4.1.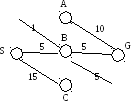

Рис. 4.1.

Найти путь минимальной стоимости из S в G.

S

C

B

A

g(n)=15

g(n)=5

g(n)=1

g(G) = 1+10=11

Попали в целевое состояние G через A, стоимость пути = 11. Смотрим, есть ли нераскрытые вершины, у которых путь меньше полученного значения.

Находим путь BG.

g(n) = 5+5=10 – более хорошее решение.

Поиск по критерию стоимости находит оптимальное решение, т. е. путь минимальной стоимости, если стоимость пути не может уменьшаться в процессе движения вдоль пути.

g(successor(n)) >=g(n)

Поиск сначала в глубину.

Поиск сначала в глубину всегда раскрывает одну из вершин на самом глубоком уровне дерева. Останавливается, когда поиск достигает цели или заходит в тупик (ни одна вершина не может быть раскрыта). В последнем случае выполняется возврат назад и раскрываются вершины на более верхних уровнях.

function Depth-First-Search(problem) returns solution or failure

General-Search(problem, En-queue-At-Front)

Сложность метода.

Для пространства состояний с коэффициентом ветвления b максимальной глубины m пространства состояний поиск в глубину требует хранение b*m вершин, поскольку нужно хранить только один путь из корня в вершину, лист и множество оставшихся ждущих раскрытия потомков.

В приведенной выше таблице для глубины d=12 поиск в ширину требует 111 Тбайт, а поиск в глубину потребует всего 12 Кбайт, но временная сложность будет b^m.

Поиск в глубину эффективнее, когда задача имеет много решений, так как в этом случае высока вероятность найти решение, исследовав малую часть пространства поиска.

Недостаток поиска в глубину – способность углубляться в неверном направлении. Многие задачи имеют очень глубокие или даже бесконечные деревья поиска, в этом случае поиск в глубину никогда не может восстановиться после неудачного выбранного вблизи корня направления. Поиск в глубину обычно реализуется с помощью рекурсивной функции.

Ограниченный по глубине поиск.

Ограниченный по глубине поиск, чтобы избежать недостатков поиска в глубину, накладывает ограничения на максимальную глубину пути.

Поиск не оптимален. Если выбрано очень малое ограничение глубины, данная стратегия даже неполна.

Временная и емкостная сложность аналогична поиску в глубину. Временная сложность O(b^L), где L – ограничение глубины.

Емкостная сложность – O(b*L)

Итеративно углубляющийся поиск.

В ограниченном по глубине поиске не всегда удается хорошо задать ограничения. В рассмотренном выше примере ограничение глубины выбиралось исходя их размерности пространства поиска. Вместе с тем может быть известна, например, максимальная длина пути для произвольной пары состояний в пространстве состояний – диаметр пространства состояний. Очевидно, что диаметр пространства является наилучшим ограничением глубины в поиске с ограничениями по глубине. Однако для большинства задач он также не известен. Итеративно углубляющийся поиск – стратегия, которая обходит выбор лучшего ограничения глубины, пробуя все возможные ограничения.

function Iterative-Deepening-Search(problem) returns solution or failure

for depth 0 to ∞ do

if Depth-Limited-Search(problem, depth)

successed then return solution

end

return failure