Конспекты лекций по Интеллектуальным системам / Л18 - Нечеткая логика

9

Лекция 18. Нечеткие множества. Лингвистическая переменная. Нечеткая логика. Нечеткий вывод. Композиционное правило вывода.

(Конспект)

В основе понятия нечеткого множества (НИ) лежит представление о том, что обладающие общим свойством элементы некоторого множества могут иметь различные степени вырожденности этого свойства и, следовательно, различную степень принадлежности этому свойству.

Пусть U некоторое множество. Нечетким множеством Ã в U называется совокупность пар вида {(µ _Ã(u), u)}, где uU, µ _Ã[0, 1].

Значение µ _Ã называется степенью принадлежности объекта к нечеткому множеству U.

µ _Ã: U  [0, 1]

µ _Ã – называется функцией принадлежности.

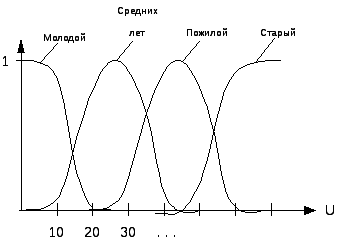
Пример нечетких множеств – возраст людей (рис. 19.1).

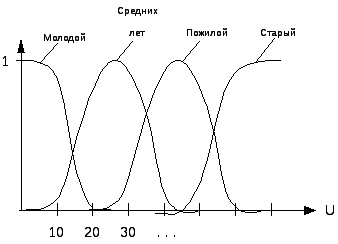
Рис. 19.1

По аналогии с традиционной теорией множеств в Теории НМ определяются следующие операции:

Объединение:

, где

Перечисление:

,

где

Дополнение:

,

Алгебраическое произведение:

, где

n-арным нечетким отношением определенным на множествах называется нечеткое подмножество декартовых произведений

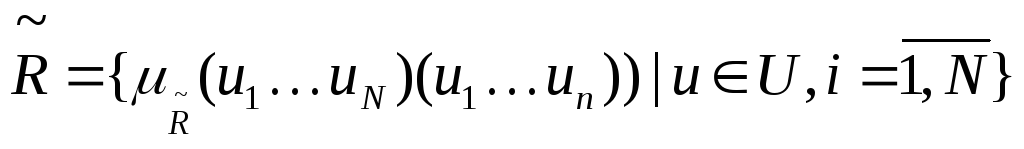
Так как нечеткое отношение является множеством для него справедливы все операции определенные для нечетких множеств. В практических приложениях теории нечетких множеств важную роль играет операция композиции нечетких отношений.

Композиция нечетких отношений

Пусть заданы 2 двухместных нечетких отношения:

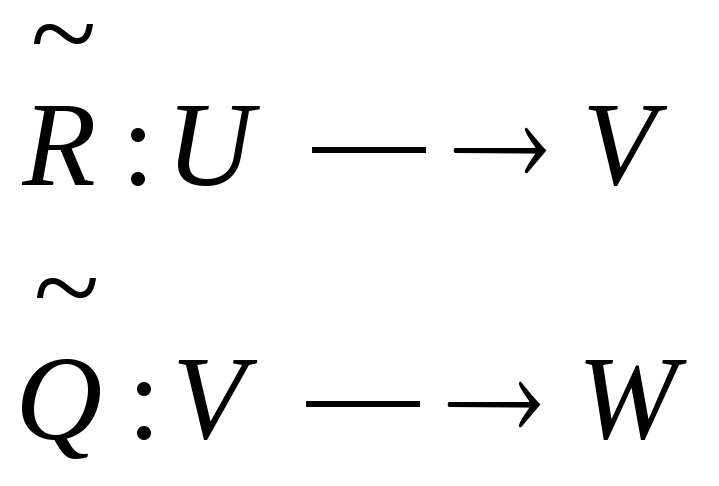
Композиция нечетких отношений определяется следующим выражением:

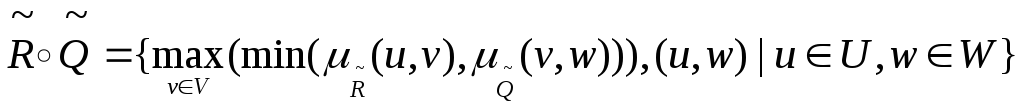
Степени принадлежности конкретных выражений

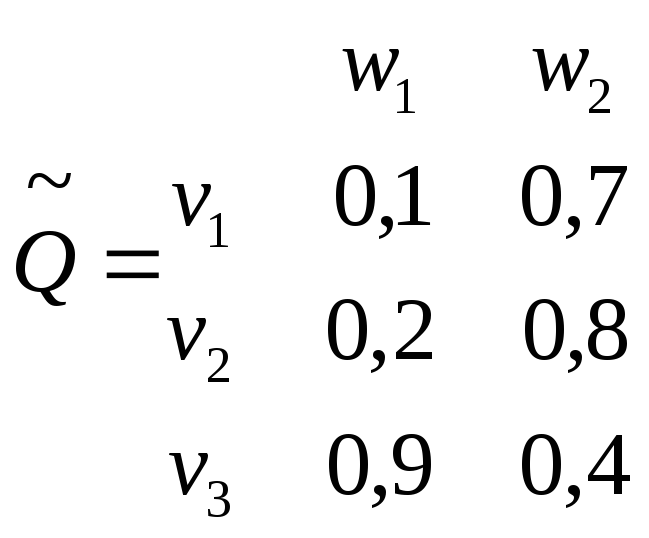
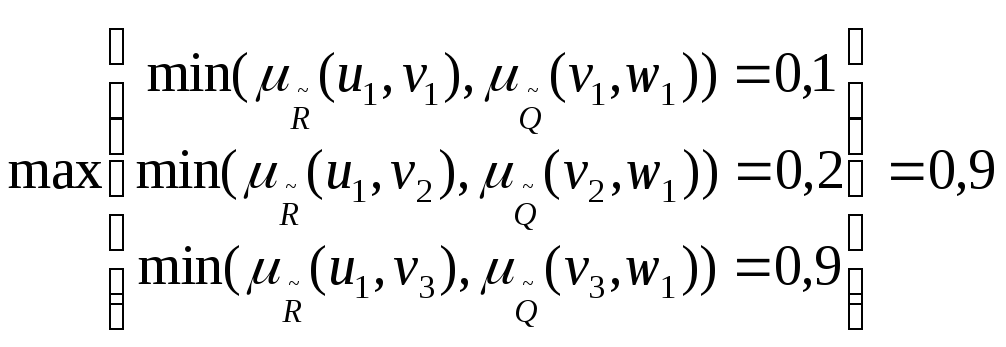
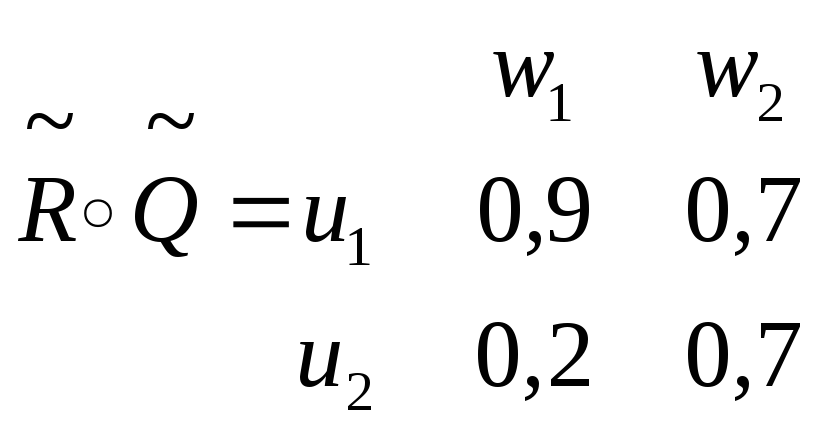
Лингвистическая переменная - <X, U, T(x), G, M> - это пятерка Х – имя переменной (возраст), U – базовое множество (0…150), Т(х) – терм множества. Множества лингвистических значений(молодой, средних лет, пожилой, старый). Каждое лингвистическое значение является меткой нечеткого множества определенного на U. G – синтаксическое правило, порождающее лингвистическое значение переменной Х (очень молодой, очень старый). М – семантическое правило ставящее в соответствие каждому лингвистическому значению нечеткое подмножество базового множества, то есть функция принадлежности.

Нечетким высказыванием называется утверждение относительно которого в данный момент времени можно судить о степени его истинности или ложности. Истинность принимает значение в интервале [0,1]. Нечеткое высказывание не допускающее разделения на более простые называется элементарным.

Нечеткое высказывание построенное на элементарных с использованием логических связок называется составным нечетким высказыванием. Логическим связкам соответствуют операции над истинностью нечетких высказываний. - степени истинности конкретных высказываний.

1)

2)

3)

Таким образом алгебра нечетких множеств изоморфна алгебре нечетких высказываний.

4) операция импликации

Для операции импликации в нечеткой логике предложено несколько определений. Основные:

1)

2)

3)

5) Эквивалентность

n-местным нечетким предикатом, определенным на множествах U₁, U₂,…,U_n называется выражение содержащее предметные переменные данных множеств и превращающиеся в нечеткие высказывания при замене предметных переменных элементами множеств U₁, U₂,…,U_n.

Пусть U₁, U₂,…,U_n базовые множества лингвистических переменных, а в качестве символов предметных переменных выступают иена лингвистических переменных. Тогда примерами нечетких предикатов являются:

1. «давление в цилиндре низкое» - одноместный предикат

2. «температура в котле значительно выше температуры в теплообменнике» - двуместных предикат.

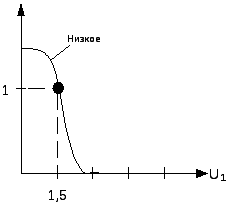
Если U_k=1,5 следовательно «давление в котле низкое» = 0,7

При построении и реализации нечетких алгоритмов важную роль играет композиционное правило вывода.

Пусть - нечеткое отображение

- нечеткое подмножество универсума U, тогда порождает в V нечеткое подмножество

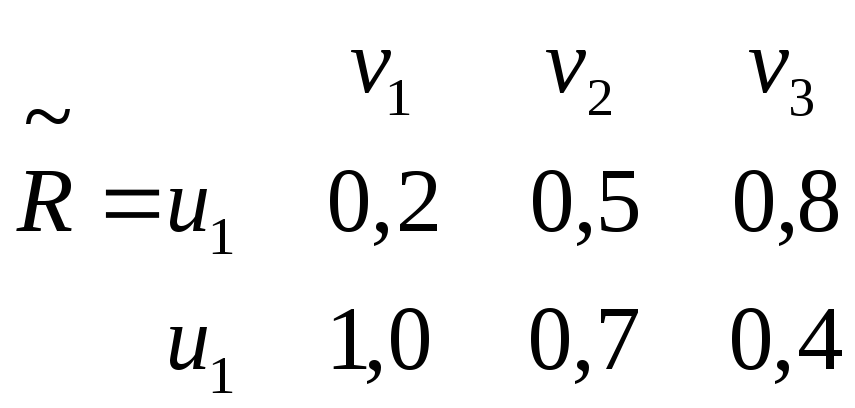
композиционное правило вывода является основой при построении логического вывода в нечеткой логике.

Пусть задано нечеткое высказывание   , где и – нечеткие множества. Пусть также того задано некоторое высказывание (близкое к А, но не тождественное ему).

В классической логике широко используется правило вывода Modus Ponens

.

Это правило обобщается на случай нечеткой логики следующим образом:

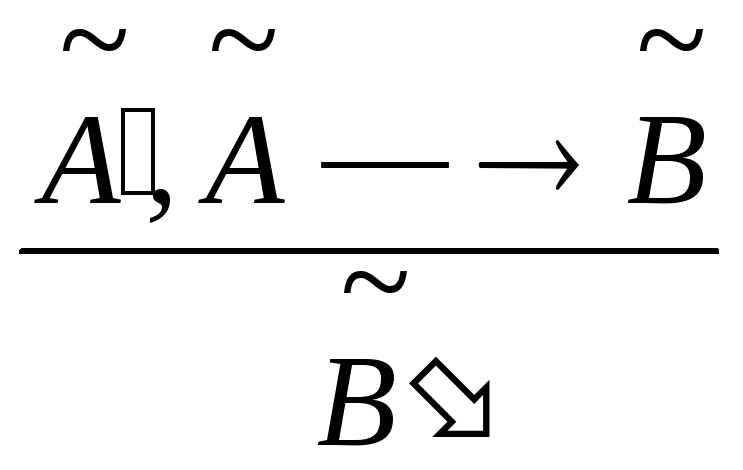
Пусть множество и определены на базовом множестве Х, а и на базовом множестве Y. Естественно считать, что высказывание если задает некоторое нечеткое отображение из множества Х в Y

Тогда в соответствии с композиционным правилом вывода имеем:

Отношение строится на основе определения операции импликации в нечеткой логики.

1)

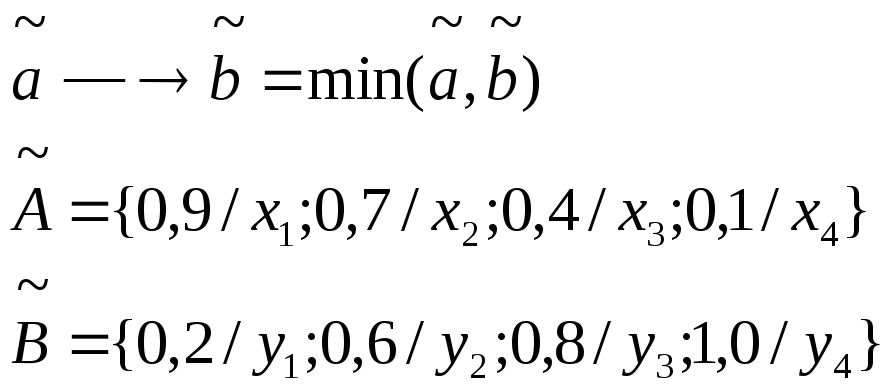
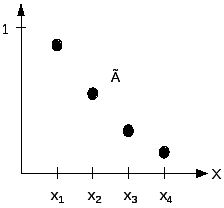
Если температура в котле низкая (), то подогрев повышенный ()

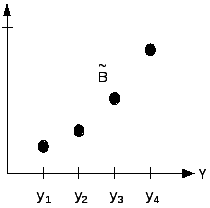
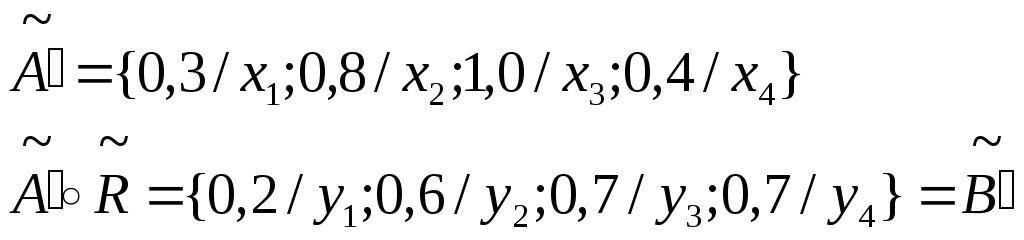
То есть

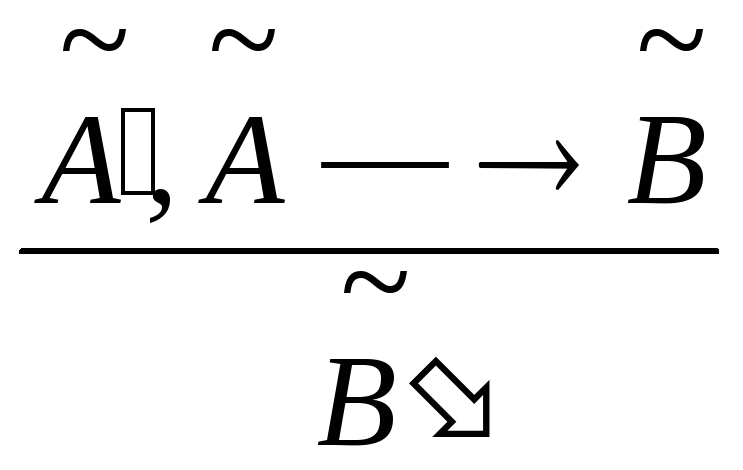
Реальные нечеткие логические алгоритмы содержат не одно, а множество продукционных правил

Если S₁, то R₁, иначе

. . .

Если S_n, то R_n, иначе

Поэтому нечеткие отношения должны быть построены для каждого отдельного правила, а затем агрегированы путем наложения друг на друга

В качестве агрегирующей операции выбирается или min или max в зависимости от типа импликации.

Когда нечеткий вывод используется в контуре управления реальным объектом, на объект должно выдаваться четкое управляющее воздействие. Поэтому необходимо преобразовать нечеткое множество, формируемое на основе композиционного правила вывода, в четкое значение. Эта процедура называется процедурой дефаззификации. Чаще используется 2 способа дефаззификации:

1) Середина «плато»

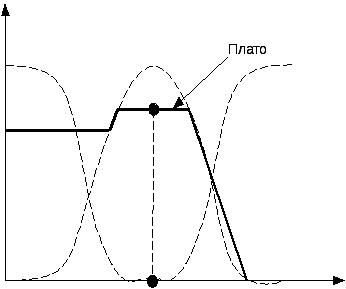
2) Центр тяжести, определяется точка которая делит площадь нечеткого множества пополам.