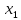- •Практикум решения задач по дисциплине «Системный анализ»
- •Решение задач Линейного программирования графическим методом
- •1.1 Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Решение задач Линейного программирования симплекс-методом
- •2.1 Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц
- •2.2 Алгоритм 2 Симплекс преобразования на основе укороченных симплекс таблиц
- •2.3 Алгоритм 3 Симплекс преобразования на основе укороченных симплекс таблиц для решения двойственной задачи Линейного программирования
- •2.4 Задача 1
- •2.5 Задача 2
- •2.6 Задача 3
- •2.7 Задача 4
- •Решение матричных игр 2xnиmx2 графоаналитическим методом
- •3.1 Задача 1 ( решение игры 2 X n)
- •3.2 Задача 2 ( решение игрыmx 2)
- •3.3 Задача 3
2.1 Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц
Изначально имеем систему неравенств
 и целевую функцию
и целевую функцию ,
для которой необходимо определить
максимум для заданной системы неравенств.
Переменные
,
для которой необходимо определить
максимум для заданной системы неравенств.
Переменные -
Свободные Переменные (СП).
-
Свободные Переменные (СП).
Чтобы свести неравенства к равенствам
к левой части неравенств
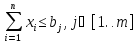 добавляют некоторую неотрицательную
величину
добавляют некоторую неотрицательную
величину .
Переменные
.
Переменные -
Базисные Переменные (БП).
-
Базисные Переменные (БП).
Тогда укороченная симплекс таблица примет вид:
|
CП БП |
|
… |
|
B |
|
|
|
… |
|
|
|
… |
… |
… |
… |
… |
|
|
|
… |
|
|
|
Z |
|
… |
|
0 |
Замечание 1:
Для дальнейшего удобства обозначим
элемент в Zстроке иBстолбце .
.
Замечание 2:
Данный алгоритм применим, если
 .
.
Выбирается разрешающий столбец lсоответствующий наименьшему отрицательному элементу вZстроке

Выбирается разрешающая строка k, которая соответствует наименьшему положительному из отношений элементов правой части уравнений на соответствующие элементы разрешающего столбца:

Замечание:
Если все отношения
 ,
значит, целевая функцияZнеограниченно возрастает и решения
нет. Необходимо прекратить симплекс
преобразование.
,
значит, целевая функцияZнеограниченно возрастает и решения
нет. Необходимо прекратить симплекс
преобразование.
Элемент стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом:

Переходим к новой симплекс таблице
 по следующим правилам:
по следующим правилам:Меняем местами СП и БП соответствующие разрешающему элементу.
На месте разрешающего элемента в новой таблице стоит величина ему обратная:

Все элементы разрешающей строки делятся на разрешающее число, включая элемент последнего столбца:

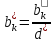
Все элементы разрешающего столбца делятся на разрешающее число, включая элемент последней строки, с обратным знаком:


Все остальные элементы матрицы
 вычисляются по формулам:
вычисляются по формулам:




Если все элементы в Zстроке
 симплекс таблицы
симплекс таблицы неотрицательны, то достигнуто оптимальное
решение, которое равно
неотрицательны, то достигнуто оптимальное
решение, которое равно .
.Если в Zстроке
 симплекс таблицы
симплекс таблицы найдется хотя бы один отрицательный
элемент, то необходимо выполнить еще
одно симплекс преобразование к симплекс
таблице
найдется хотя бы один отрицательный
элемент, то необходимо выполнить еще
одно симплекс преобразование к симплекс
таблице ,
согласно п.1-6 приведенного выше алгоритма.
,
согласно п.1-6 приведенного выше алгоритма.
2.2 Алгоритм 2 Симплекс преобразования на основе укороченных симплекс таблиц
Рассмотрим
симплекс-метод для решения задачи
Линейного программирования в случае,
если существует
 .
.
Изначально
имеем систему неравенств
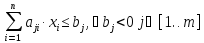 и целевую функцию
и целевую функцию ,
для которой необходимо определить
максимум для заданной системы неравенств.
Переменные
,
для которой необходимо определить
максимум для заданной системы неравенств.
Переменные -
Свободные Переменные (СП). Данную систему
неравенств необходимо привести к виду,
где
-
Свободные Переменные (СП). Данную систему
неравенств необходимо привести к виду,
где . А затем к приведенной системе применить
“Алгоритм 1 Симплекс преобразования
на основе укороченных симплекс таблиц”
. А затем к приведенной системе применить
“Алгоритм 1 Симплекс преобразования
на основе укороченных симплекс таблиц”
Тогда укороченная симплекс таблица примет вид:
|
СП БП |
|
… |
|
B |
|
|
|
… |
|
|
|
… |
… |
… |
… |
… |
|
|
|
… |
|
|
|
Z |
|
… |
|
0 |
Выбрать строку с наименьшим отрицательным свободным членом в B-столбце

Рассмотреть элементы s-ой строки.
Если
 , следовательно, система несовместна,
и задача Линейного программированияне имеет решений
, следовательно, система несовместна,
и задача Линейного программированияне имеет решенийЕсли
 ,то
необходимо взятьлюбой
,то
необходимо взятьлюбой и столбец, содержащий данный элемент
в качестве разрешающего столбца –
и столбец, содержащий данный элемент
в качестве разрешающего столбца – .
.
Выбирается разрешающая строка k, которая соответствует наименьшему положительному из отношений элементов правой части уравнений на соответствующие элементы разрешающего столбца:

Тогда элемент, стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом
 .
.
Замечание:В случае, когда ,
то элемент
,
то элемент выбирается в качестве разрешающего
только в том случае, если
выбирается в качестве разрешающего
только в том случае, если иначе
произойдет зацикливание. Если же
иначе
произойдет зацикливание. Если же ,
, и в строкеsкроме элемента
и в строкеsкроме элемента есть еще элемент
есть еще элемент и при этом
и при этом ,
то в качестве разрешающего столбца
лучше брать столбецr. И
тогдаk-я строка уже не
будет разрешающей.
,
то в качестве разрешающего столбца
лучше брать столбецr. И
тогдаk-я строка уже не
будет разрешающей.
Далее выполняем все п.4 “Алгоритм 1 Симплекс преобразования на основе укороченных симплекс таблиц”.
Если в результате симплексного преобразования в столбце свободных членов B все еще есть отрицательные элементы, то необходимо применять п. 1-5 “Алгоритм 2 Симплекс преобразования на основе укороченных симплекс таблиц” до тех пор пока все элементы столбца свободных членов не будут положительными
Если в результате симплексного преобразования в столбце свободных членов B нет отрицательных элементов, тогда перейти к применению “Алгоритма 1 Симплекс преобразования на основе укороченных симплекс таблиц” (п.1-6)