Лабораторные работы / 1 / Линеаризация

1.4. Линеаризация уравнений

Основная сложность при выводе уравнений реальных звеньев заключается в определении допустимой степени идеализации и упрощения. Основная цель упрощения - линеаризация нелинейности уравнения реального звена, т.е замена реального уравнения его приближённой линейной зависимостью.

На практике используют два основных метода линеаризации нелинейных систем:

• линеаризация разложением в ряд Тейлора, для малых возмущений в окрестностях рабочей точки;

• гармоническая линеаризация с целью выявления автоколебаний в нелинейных системах.

Задача линеаризации разложением в ряд Тейлора, для малых возмущений в окрестностях рабочей точки сводится к нахождению производной в заданной точке и нахождения допустимых отклонений режима от рабочей точки.

Функцию y = (x), непрерывную и имеющую все производные при х = х₀, можно представить в виде суммы степенного ряда, получающегося из разложения по формуле Тейлора.

. (1.4.1)

Используя два первых члена разложения и обозначив х – х₀ = Dx получим

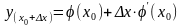. (1.4.2)

Уравнение (1.4.2), по форме является линейным и называется линеаризованным уравнением нелинейной функции (x).

Обозначив y(x₀+x) – y(x₀) = y и вычтя из левой и правой частей уравнения (1.4.2) значение y(x₀) получим

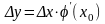. (1.4.3)

Уравнение (1.4.3) называется линеаризованным уравнением в отклонениях. Уравнение (1.4.3) описывает ту же исходную функцию (x), но отличается от исходного уравнения в следующем:

• Переменными в уравнении (1.4.3) являются не прежние полные переменные x и y, а их отклонения x и y.

• Полученное уравнение является линейным относительно отклонений x и y.

• Уравнение (1.4.3) описывает функцию в ограниченной области изменений х вблизи рабочей точки.

• Уравнение (1.4.3) описывает исходную функцию приближённо, с точностью до значения остаточного члена

,

где коэффициент  может выбираться в пределах от 0 до 1, т.е. 0<<1.

Выражение для остаточного члена справедливо при условии, что ряд сходится и остаточный член R_n  0 при n  .

При использовании только первых двух членов ряда и при условии, что x>>x остаточный член разложения

.

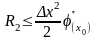Относительная погрешность линеаризации получается

.

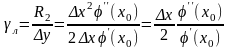Отсюда допустимое значение отклонения x

.

Допустимость такой линеаризации возможна только при соблюдении очевидных условий:

• малости отклонений, погрешность линеаризации растёт с ростом отклонения;

• нелинейная характеристика должна быть непрерывно дифференцируемой;

• ряд Тейлора должен сходиться и второй член разложения должен быть меньше первого.

Нелинейные характеристики, не удовлетворяющие этим условиям, называются существенно нелинейными. К ним относятся прерывистые характеристики типа релейных и неоднозначные характеристики типа петли гистерезиса.

Исследование разложения на сходимость является сложной математической задачей, поэтому для проверки правомерности применения этого способа линеаризации следует проверить фактическую погрешность линеаризации при значениях отклонения x_доп.

.

Из геометрической интерпретации следует ещё один способ линеаризации - геометрический, заключающийся в том, что все криволинейные зависимости, при составлении уравнения графически заменяются прямолинейными, по касательной к рабочей точке.

Условия задачи:

• задана функция y = (x);

• определена рабочая область в виде непрерывного множества значений x = {x_min...x_max};

• задана рабочая точка х₀;

• задана допустимая погрешность линеаризации.

Требуется:

• построить график заданной функции в диапазоне рабочих значений аргумента;

• найти линеаризованное уравнение в окрестностях заданной точки;

• записать линеаризованное уравнение в отклонениях;

• найти допустимое значение отклонения аргумента при заданном значении погрешности линеаризации;

• построить зависимость фактической относительной ошибки линеаризации от значения отклонения аргумента в пределах допустимых значений.

Рекомендуемый алгоритм решения.

1. Находим y(x₀) = ?.

2. Находим y'(x) = ? и y'(x₀) = ?.

3. .Находим y''(x) = ? и y''(x₀) = ?.

4. Находим точки экстремумов из уравнения y'(x) = 0.

5. Находим значения у для точек: y(x_экстр), у(x_min), у(x_max).

6. Строим график y = (x).

7. Составляем линеаризованное уравнение y_л = у(x₀)+ху'(x₀).

Полученное уравнение по форме является линейным уравнением и соответствует уравнению (1.2). Коэффициент b = у(x₀), коэффициент K = у'(x₀), а переменная х заменяется отклонением от рабочей точки х, поэтому это уравнение иногда называют уравнением в отклонениях.

8. Так как наклон прямой не зависит от коэффициента b, то часто используют сокращенную форму записи, оставляя только приращения аргумента и функции. Линеаризованное уравнение в приращениях имеет вид:

y_л = Kх, K = у'(x₀).

9. Находим х_доп при _доп = 10%.

.

10. Находим фактическую относительную погрешность линеаризации

.

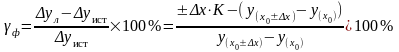10. Строим график зависимости фактической относительной погрешности линеаризации от значения отклонения х в пределах изменений от 0 до .х_доп.

Пример решения №1.1

Заданы:

у = 8х – х²; х₀ = 2;

x = {0 - 4}; _доп = 10%.

Решение.

1. у = 8х – х²; у₀ = у_{(х = 2)} = 12;

2. y'(x) = 8 – 2х; y'_{(х = 2)} = 4;

3. y''(x) = –2; y''_{(х = 2)} = –2;

4. Находим точку экстремума

8 – 2х = 0;

8 = 2х;

х = 4;

5. Находим значения некоторых точек для построения графика

у_{(х = 0)} = 0; у_{(х = 2)} = 12;

у_{(х = 3)} = 15; у_{(х = 4)} = 16; у_{(х = 5)} = 15;

6. Строим график (рис.1.9)

Рис.1.9. График функции у = 8х – х²;

7. Составляем линеаризованное уравнение

у_{(х = 2 + х)} = 12 + 4х;

8. Составляем уравнение в приращениях

у = 4х; при х = 2.

9. Находим максимальное допустимое отклонение х при погрешности 10%

.

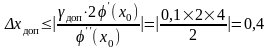10. Находим фактическую относительную погрешность линеаризации для четырёх точек х = х_доп и х = х_доп/2:

х₀ = 2; у_{(х = 2)} = 12;

х = +0,4: х = 2,4; у_{(х = 2,4)} = 13,44;

;

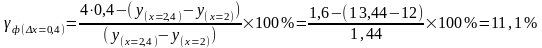х = –0,4: х = 1,6; у_{(х = 1,6)} = 10,24;

;

х = х_доп/2;

х = +0,2: х = 2,2; у_{(х = 2,2)} = 12,76;

;

;

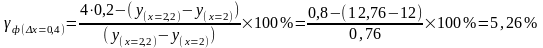11. Строим график зависимости относительной погрешности линеаризации от отклонения х

Рис.1.10. График погрешности линеаризации

Пример решения №1.2

Заданы:

i = S(u + 16)^3/2; S = 0,5 u = [–14...0];

u₀ = –6; _л,зад  10%.

Решение.

1. i = 0,5(u + 16)^3/2; i_{(u = –6)} = 15,81;

2. i'(u) = 0,75(u + 16)^1/2; i'_{(u = –6)} = 2,37;

3. i''(u) = 0,375(u + 16)^–1/2; i''_{(u = –6)} = 0,12;

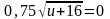4. ; ; u + 16 = 0; u_экст = –16;

5. i_{(u = –16)} = 0; i_{(u = –10)} = 7,35; i_{(u = –6)} = 15,81; i_{(u = 0)} = 32;

Рис.1.11. График функции i = 0,5(u + 16)^3/2;

7. i_л = 15,81 + 2,37u;

8. i = 2,37u;

9. |u_доп|  3,95;

u₀ = –6; i_{(u = –6)} = 15,81;

u = +3,95; u = –2,05; i_{(u = –2,05)} = 26,05;

;

u = –3.95; u = –9,95; i_{(u = –2,05)} = 7,44;

;

u = u_доп/2; u = +2; u = –4; i_{(u = –4)} = 20,79;

;

u = u_доп/2; u = –2; u = –8; i_{(u = –8)} = 11,31;

;

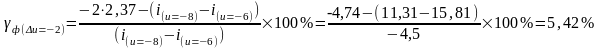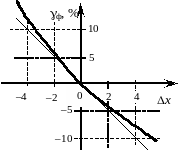
Рис.1.12. График погрешности линеаризации

Справочный материал

(xⁿ)' = nx^n–1; e⁸ = 2981;

(e^x)' = e^x; e⁴ = 54,6;

(uv)' = uv' + u'v; e² = 7,39;

Если y = f(u) и u = (x), то dy/dx = f '(u)'(x); e^–0,5 = 0,61;

e^–0,6 = 0,55;

(1/xⁿ)' = –n/xⁿ⁺¹; e^–1,2 = 0,3;

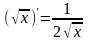; e^–1,5 = 0,22;

(1/x)' = –1/x²;