1.5. Форсирующее звено

Форсирующим называется звено, дифференциальное уравнение которого имеет вид

.

(1.32)

Нетрудно убедиться в том, что (1.32) можно представить как сумму уравнений пропорционального и дифференцирующего звеньев.

Передаточную функцию форсирующего звена

принято записывать в стандартной форме

(1.33)

где - коэффициент усиления, а - постоянная времени звена.

Передаточная функция (1.33) содержит полином в числителе, корень которого называется «нулем» форсирующего звена.

Его переходная характеристика определяется соотношением

.

(1.34)

Качественный вид ее приведен на рис. 1.17.

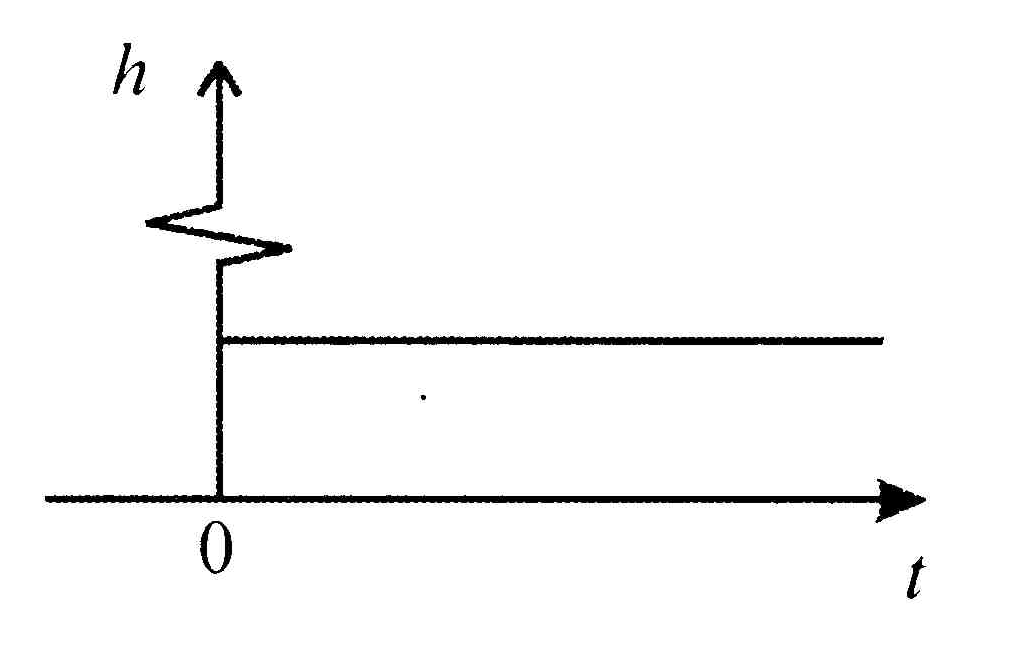
Рис.1.17. Переходная характеристика форсирующего звена.

Импульсная переходная функция звена следующая:

.

(1.35)

Обобщенная частотная характеристика находится по передаточной функции (1.33) и имеет вид

.

(1.36)

Соответствующая амплитудно-фазовая характеристика изображена на рис.1.18.

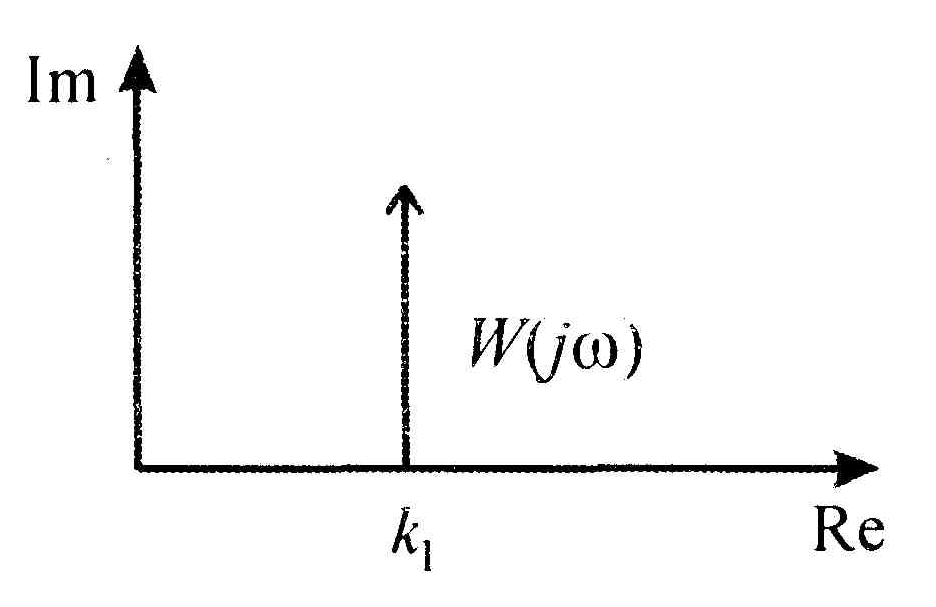
Рис.1.18. Амплитудно-фазовая характеристика

форсирующего звена.

Вещественная частотная характеристика звена не зависит от частоты и равна , мнимая частотная характеристика представляет собой прямую

.

Амплитудная частотная характеристика может быть построена по выражению

,

а фазовая частотная характеристика определяется в виде

(1.37)

причем в пределе .

На основании выражения для определим логарифмическую амплитудную частотную характеристику

.

(1.38)

Как и в предыдущем случае, для форсирующего звена удобнее строить не точную, а асимптотическую ЛАЧХ (рис. 1.19). Здесь - собственная частота звена.

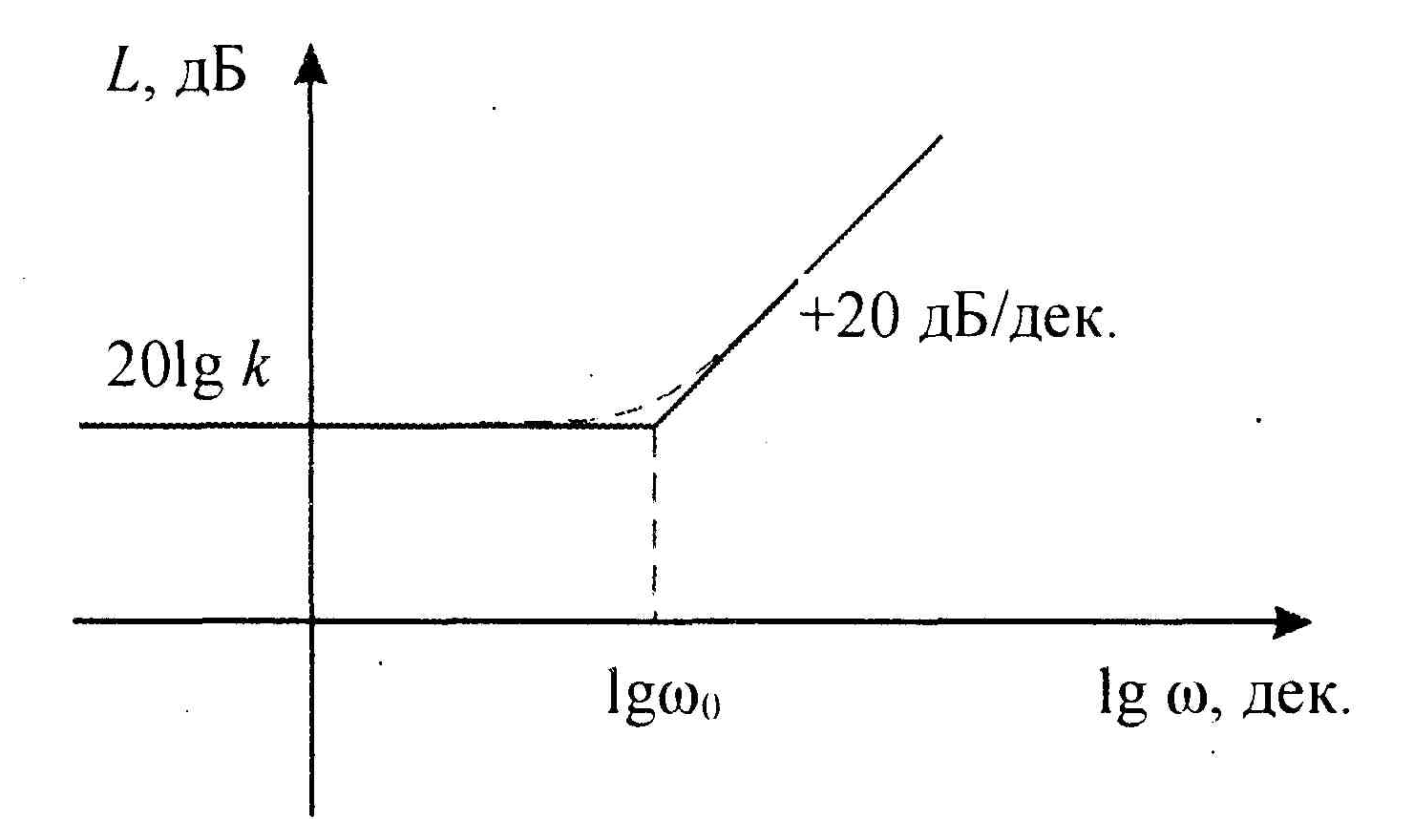
Рис.1.19. Логарифмическая амплитудная частотная

характеристика форсирующего звена.

Причем ее можно получить, исследуя отдельно области низких и высоких частот или суммируя ЛАЧХ пропорционального и дифференцирующего звеньев.

Нетрудно убедиться, сравнивая выражения (1.28) и (1.29) с выражениями (1.37) и (1.38), в том, что логарифмические амплитудная и фазовая частотные характеристики форсирующего звена представляют собой зеркальное отображение относительно оси абсцисс соответствующих логарифмических характеристик апериодического звена.

1.6. Звено второго порядка

Дифференциальное уравнение звена второго порядка

(1.39)

принято записывать в стандартном виде

(1.40)

где - постоянная времени звена; - коэффициент демпфирования, который определяет склонность переходных процессов к колебаниям, , - коэффициент усиления.

Передаточную функцию звена получим на основе символической записи дифференциального уравнения

в виде

(1.41)

Для определения модальных характеристик запишем характеристическое уравнение звена

.

(1.42)

Оно имеет два корня (полюса), которые в зависимости от коэффициента демпфирования , могут быть вещественными или комплексно-сопряженными, что приводит к различным переходным процессам. Рассмотрим варианты корней.

1. Если , то корни уравнения (1.42) вещественные и положительные. Обозначим их через , и получим переходную функцию (рис.1.20) в виде

.

(1.43)

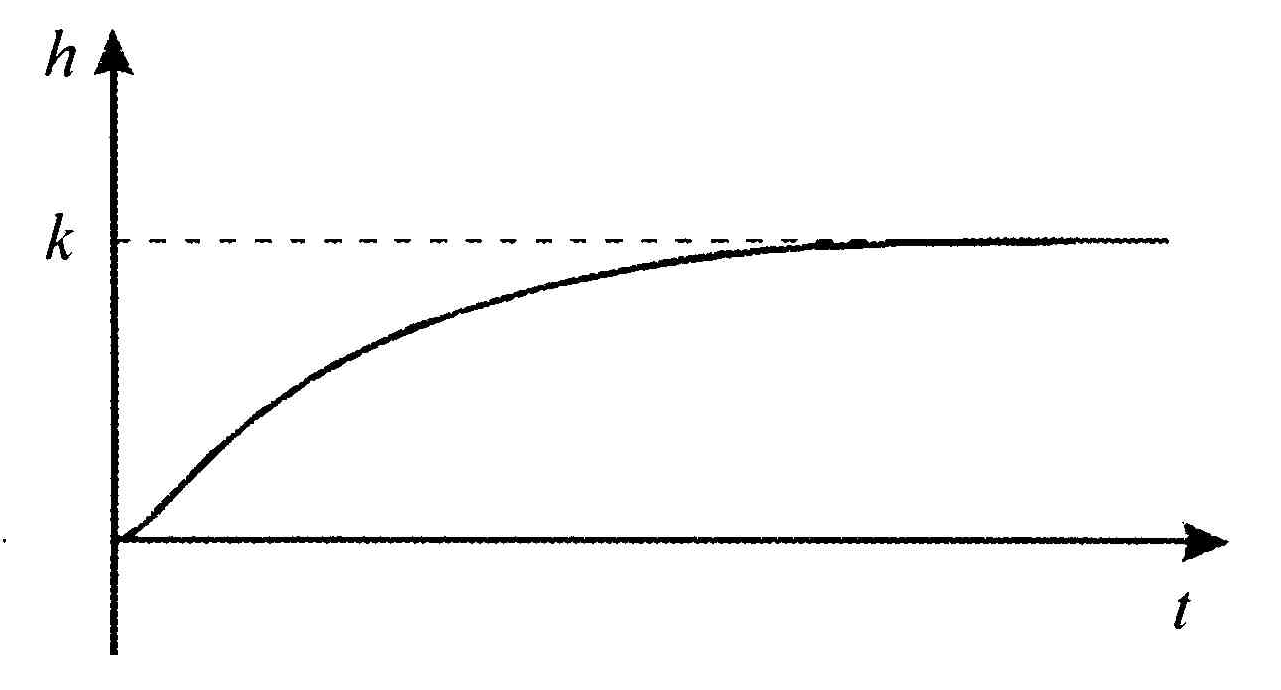
Рис.1.20. переходная характеристика звена второго

порядка при .

2. Если, то корни уравнения (1.42) будут комплексно-сопряженными, т.е. ( ). При получаем .

В случае, когда коэффициент демпфирования изменяется в диапазоне , звено второго порядка называют колебательным. Выражение для его переходной характеристики следующее:

.

(1.44)

Причем колебательность переходного процесса будет тем больше, чем меньше коэффициент демпфирования . В пределе при будут иметь место незатухающие колебания. В этом случае звено называется консервативным. Соответствующие графики переходных процессов представлены на рис. 1.21.

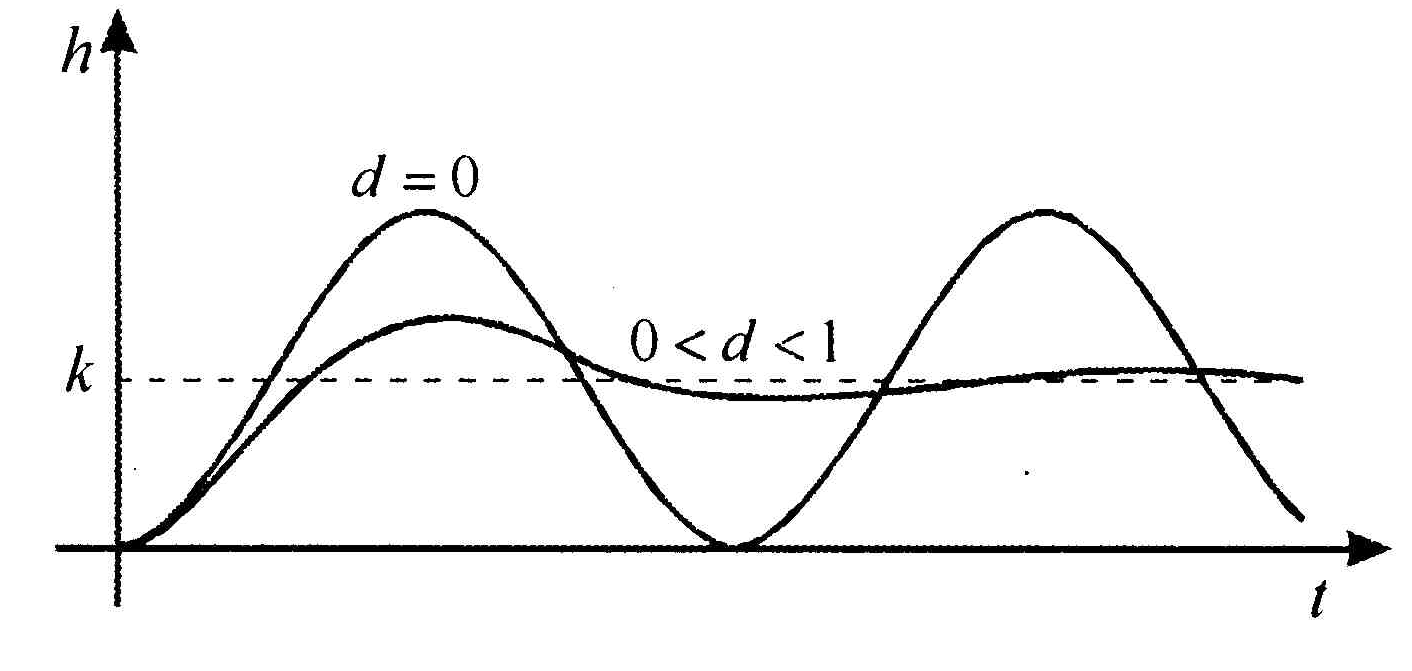
Рис.1.21. переходная характеристика звена при .

Определим выражение для общей частотной характеристики колебательного звена, заменив на в передаточной функции (1.41):

.

(1.45)

Запишем выражения для вещественной частотной характеристики

(1.46)

и мнимой частотной характеристики:

(1.47)

На основе (1.46) и (1.47) построим АЧХ на комплексной плоскости, рассматривая характерные точки: , , ... , . Ее вид существенно зависит от коэффициента демпфирования (рис. 1.22).

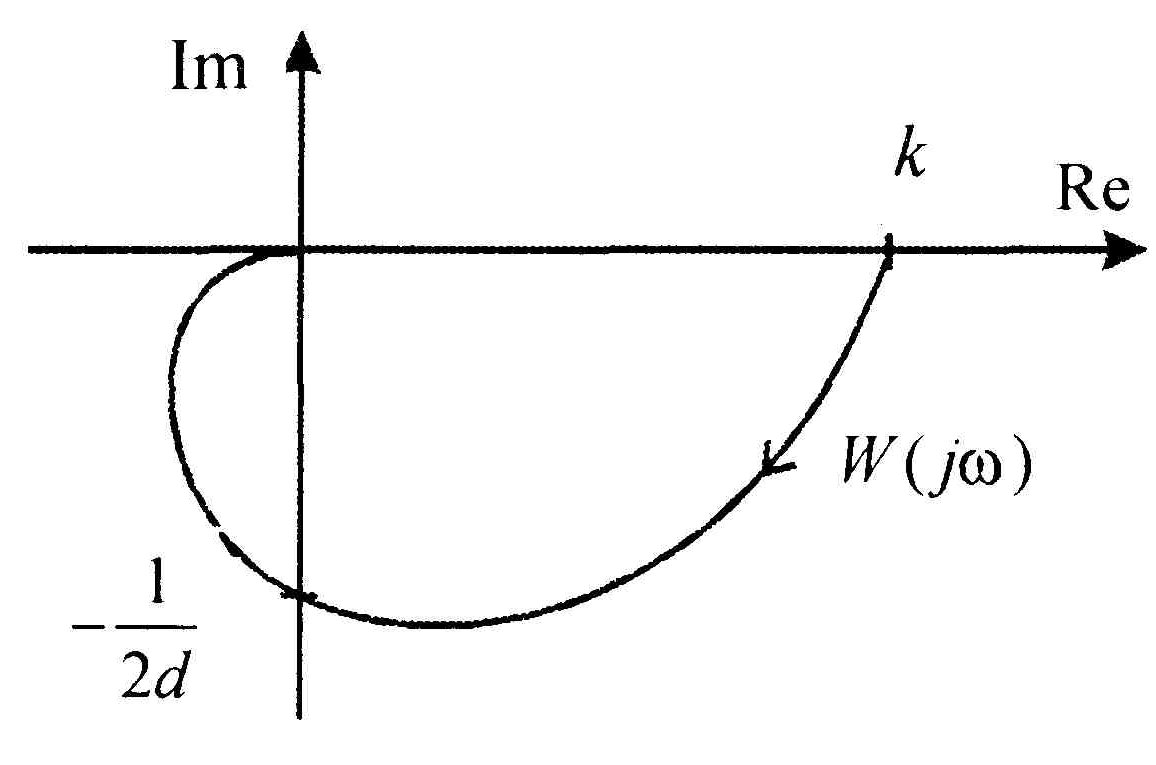
Рис.1.22. Амплитудно-фазовая характеристика

звена второго порядка.

Амплитудно-фазовая характеристика консервативного звена ( ) начинается в точке на вещественной оси и при увеличении стремится к , а затем из - к началу координат.

Амплитудная частотная характеристика строится на основе выражения

(1.48)

и может иметь резонансный пик, высота которого будет тем больше, чем меньше коэффициент демпфирования А.

Формула для фазовой частотной характеристики имеет вид

.

(1.49)

Построение ЛАЧХ колебательного звена (при ) осуществляется по соотношению, полученному из (1.48):

.

(1.50)

При значениях коэффициента демпфирования в интервале можно строить упрощенную асимптотическую ЛАЧХ, рассматривая отдельно области высоких и низких частот.

В области низких частот ( ) асимптота имеет вид

.

В области высоких частот, когда , получим вторую асимптоту (рис.1.23).

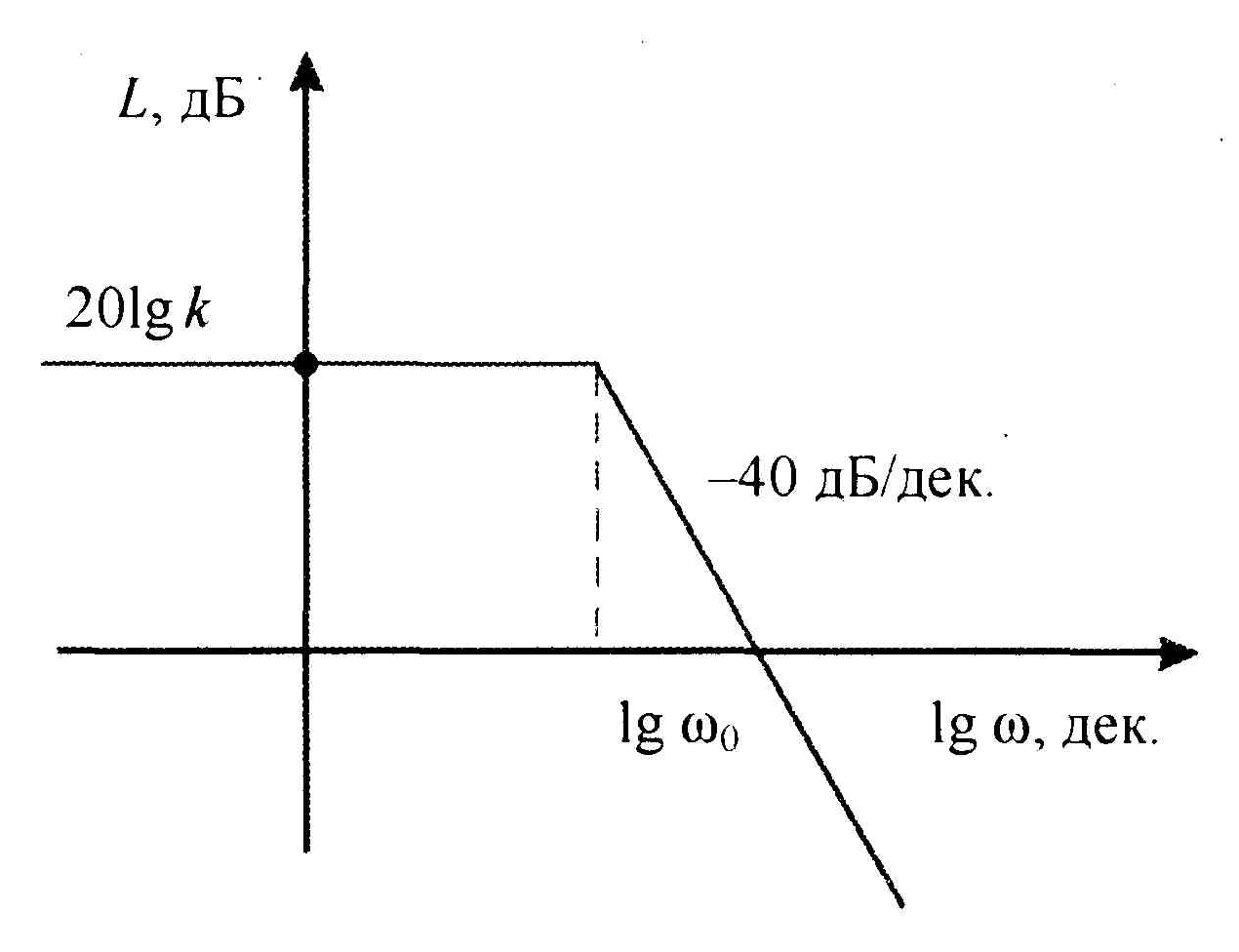
Рис.1.23. Асимптотическая ЛАЧХ колебательного

звена при .

На собственной частоте колебательного звена справедливо соотношение .

Наибольшее отличие асимптотической ЛАЧХ от действительной характеристики наблюдается на частоте (рис.1.24) от величины коэффициента демпфирования.

При значениях не следует пользоваться асимптотической ЛАЧХ, а нужно строить точную логарифмическую характеристику.

При корни характеристического уравнения (1.42) будут вещественными и передаточную функцию звена второго порядка (1.41) можно представить в виде произведения двух передаточных функций апериодических звеньев:

(1.51)

где , - постоянные времени апериодических звеньев. В этом случае асимптотическая ЛАЧХ звена второго порядка имеет два «излома» на частотах , .

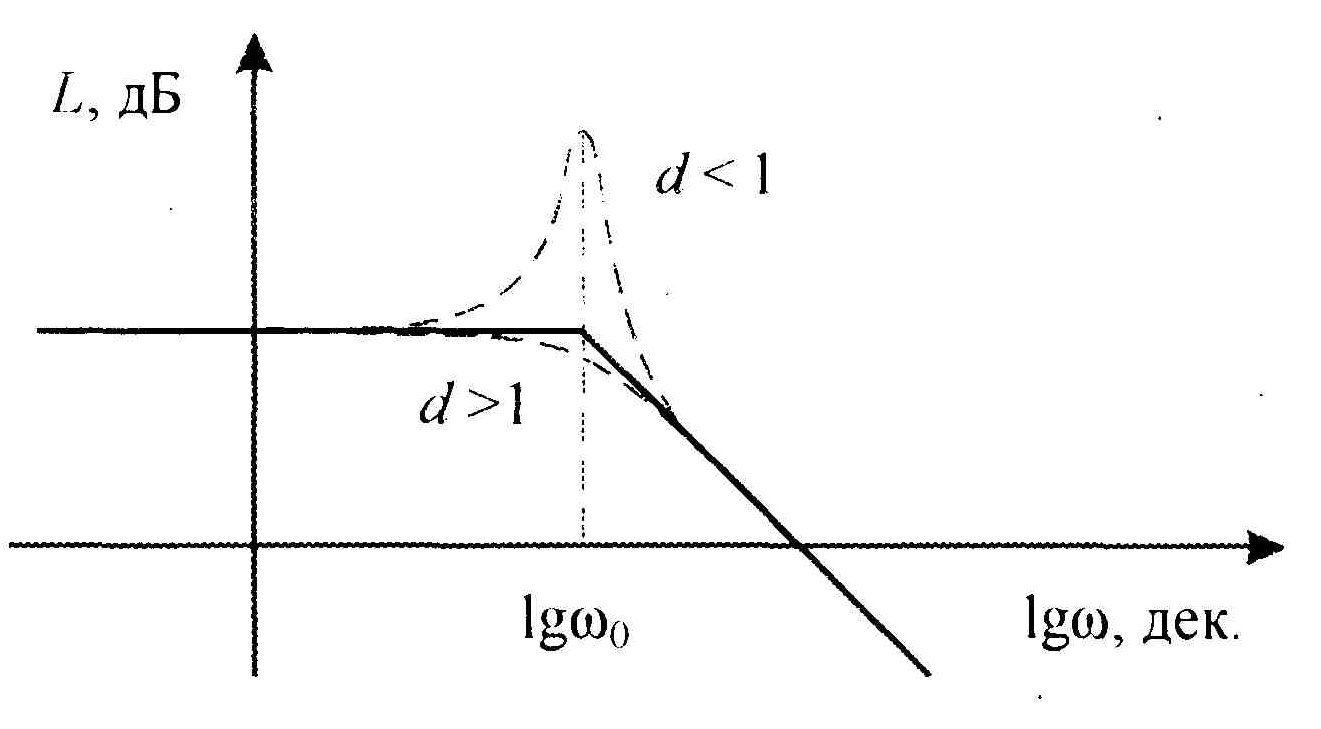
Рис.1.24. Влияние коэффициента демпфирования

на ЛАЧХ звена.

Она может быть получена суммированием асимптотических ЛАЧХ двух апериодических звеньев.

Вышерассмотренные характеристики приведены в таблицах 1.1 и 1.2.

Таблица 1.1