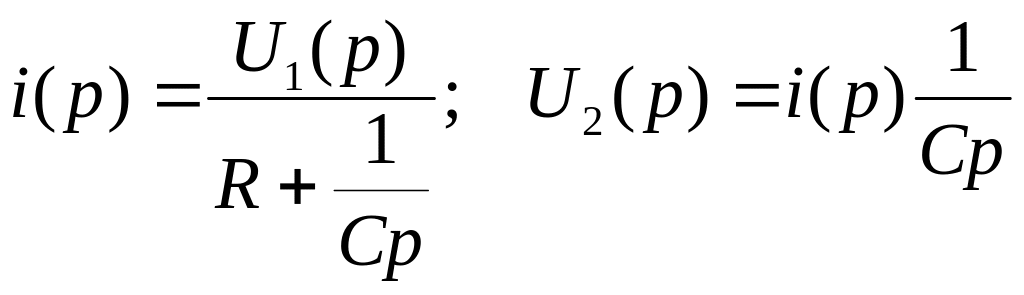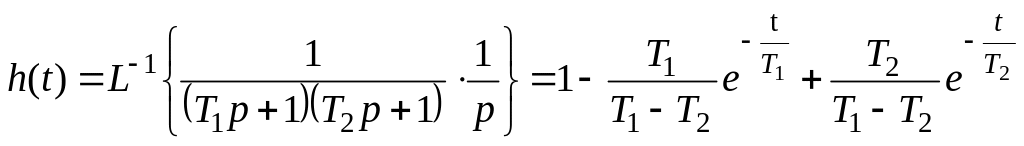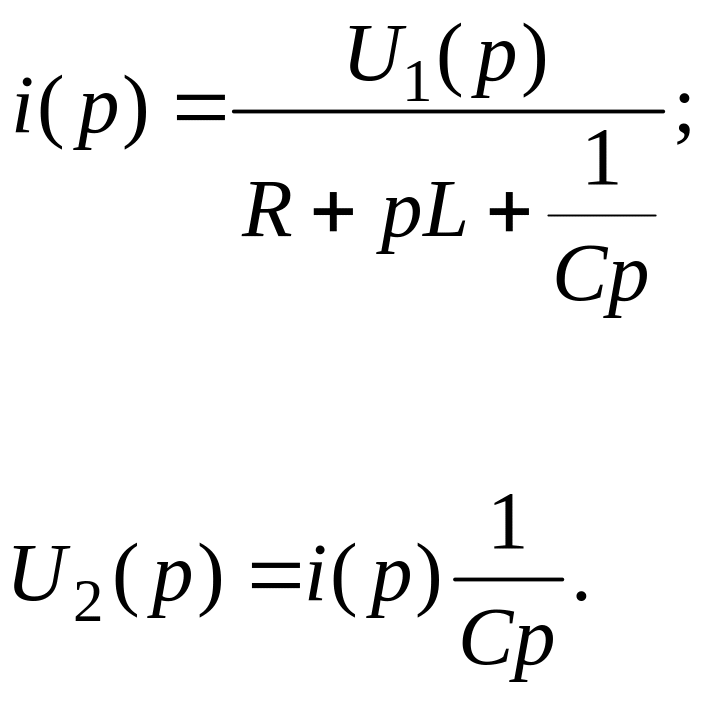Типовые динамические звенья

При анализе и синтезе САУ целесообразно представлять сложную передаточную функцию системы в виде произведения элементарных передаточных функций – типовых звеньев (11)

,

(11)

где

.

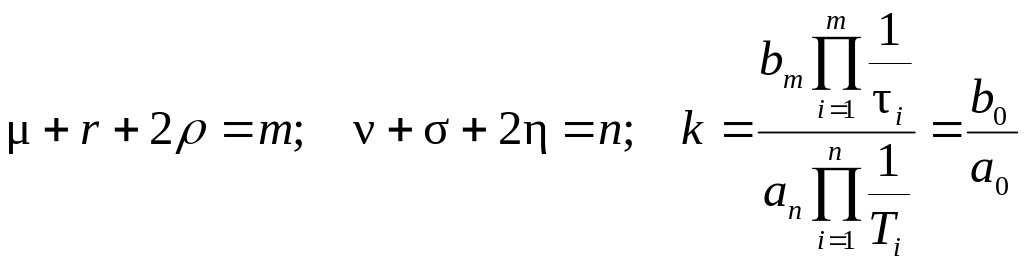Расчленение САУ на типовые звенья имеет не только формальную математическую, но и техническую основу. Целесообразность разбиения динамического элемента на типовые звенья объясняется особенностью технической реализации САУ, состоящих обычно из совокупности сравнительно несложных устройств направленного действия, описываемых дифференциальными уравнениями первого и второго порядков.

Звенья, имеющие передаточные функции, соответствующие трем типам сомножителей, входящих в знаменатель, будем называть интегрирующими, апериодическими и колебательными.

Звенья, имеющие передаточные функции, которые соответствуют четырем типам сомножителей числителя, будем называть усилительными, идеальными дифференцирующими, форсирующими первого порядка и форсирующими второго порядка.

Кроме того, многие реальные элементы САУ имеют передаточные функции, достаточно близкие к передаточным функциям типовых звеньев. Следовательно, анализ динамики таких элементов значительно упрощается.

Рассмотрим основные типовые звенья, которые наиболее часто встречаются на практике.

Апериодическое (инерционное) звено

Дифференциальное уравнение апериодического звена:

(12)

Уравнению (12) соответствует передаточная функция апериодического звена:

(13)

Переходную функцию получим из (10):

(14)

Вид переходной характеристики апериодического звена представлен на рис.3.

Параметр Т имеет размерность времени и называется постоянной времени.

Рисунок 3 иллюстрирует графическое определение постоянной времени Т по экспериментальной переходной функции апериодического звена.

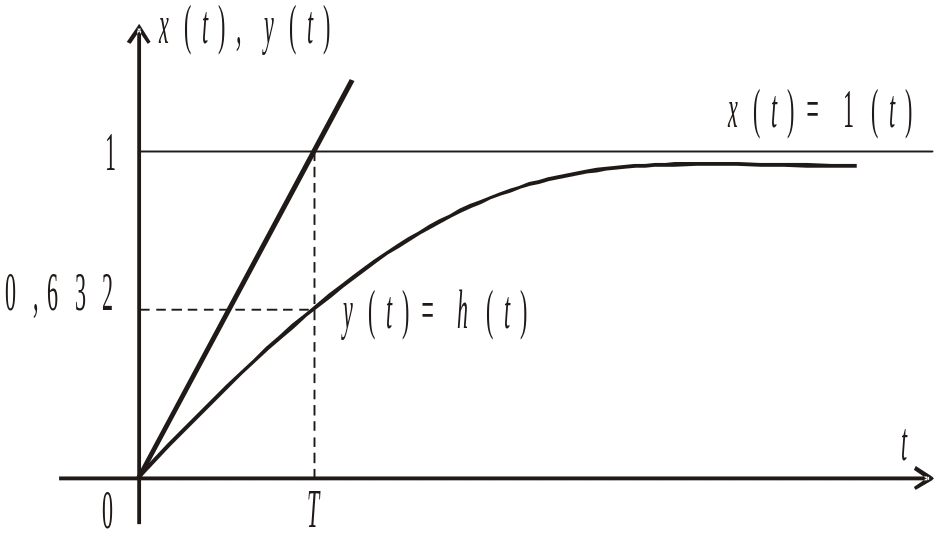
Рис. 3. Переходная характеристика апериодического звена.

Касательная, проведенная к h(t) при t = 0 пересекает ординату 1 при t=T. Тогда:

В таблице 1 приведены значения h(t) в моменты времени, кратные Т, из которой видно, что переходный процесс в апериодическом звене можно считать закончившимися при t ≥ 3T.

Таблица 1

Значения переходной характеристики

t	T	2T	3T	4T	5T
h(t)	0,63	0,86	0,95	0,98	0,993

Постоянная времени апериодического звена определяется из эксперимента по осциллограмме. На лабораторном стенде апериодическое звено реализовано на R, C элементах (рис.4).

Рис. 4. Апериодическое звено на RC элементах.

Передаточную функцию звена получим из уравнений:

где T=RC; [T]=[R][C] = Ом·Ф = сек.

Аналогично передаточную функцию апериодического звена на R, L элементах (рис.5) получим из уравнений:

где T = L/R, [T]=[L]/[R] = ГнОм = сек.

Рис. 5. Апериодическое звено на RL-элементах.

Дифференцирующее звено первого порядка

Идеальным дифференцирующим звеном первого порядка называется звено, имеющее передаточную функцию вида:

,

(15)

которой соответствует дифференциальное уравнение

.

Звено с передаточной функцией (15) является физически нереализуемым (m>n). На практике дифференцирующие звенья имеют передаточную функцию:

,

(16)

которой соответствует дифференциальное уравнение:

Переходная функция реального дифференцирующего звена имеет вид:

(17)

График переходной характеристики приведен на рис.6. Способ определения параметра Т тот же, что и для апериодического звена.

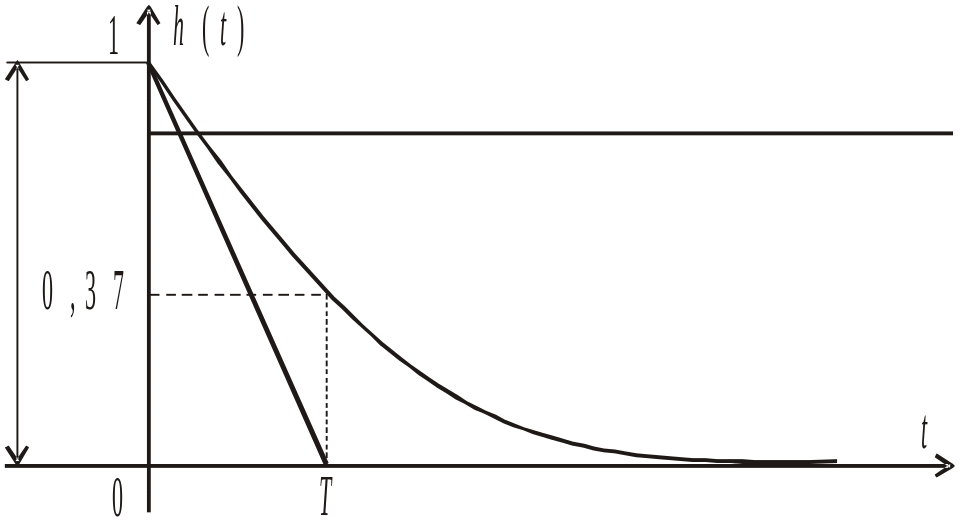
Рис. 6. Переходная характеристика дифференцирующего

звена первого порядка.

На рисунке 6 видно: касательная к h(t) при t = 0 пересекает ось абсцисс при t = T. Тогда h(t) = e^-1=0,37.

Постоянная времени дифференцирующего звена первого порядка определяется из эксперимента по осциллограмме. На лабораторном стенде дифференцирующее звено первого порядка реализовано на R, C элементах (рис.7).

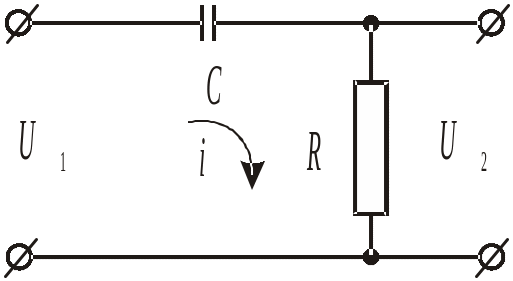
Рис. 7. Дифференцирующее звено первого порядка

на RC-элементах.

Передаточная функция этого звена:

,

где T=RC.

Аналогично передаточная функция дифференцирующего звена 1-го порядка, реализованная на RL-элементах (рис.8), определяется следующим образом:

,

где .

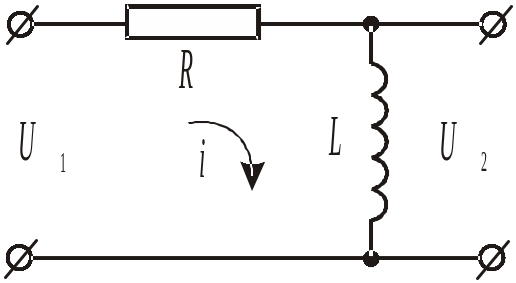
Рис. 8. Дифференцирующее звено первого порядка

на RL-элементах.

Переходная характеристика, реализованных для звеньев RC и RL (рис.7, 8), определяется из выражения:

(18)

Колебательное звено

Колебательным звеном называется звено второго порядка, имеющее передаточную функцию

.

(19)

Дифференциальное уравнение колебательного звена

,

(20)

где 0≤ξ<1.

Характеристическое уравнение, соответствующее дифференциальному уравнению (20) имеет следующий вид:

корни этого уравнения определяются зависимостью

.

(21)

Из выражения (21) следует, что при корни и получаются комплексными, следовательно, для решения уравнения (20) будет характерна колебательная составляющая, а при корни и - действительные отрицательные и собственное решение уравнения (20) будет иметь затухающий апериодический характер.

Определим переходную функцию колебательного звена. Согласно (10) имеем:

,

(22)

где

.

Переходная характеристика колебательного звена показана на рис.9.

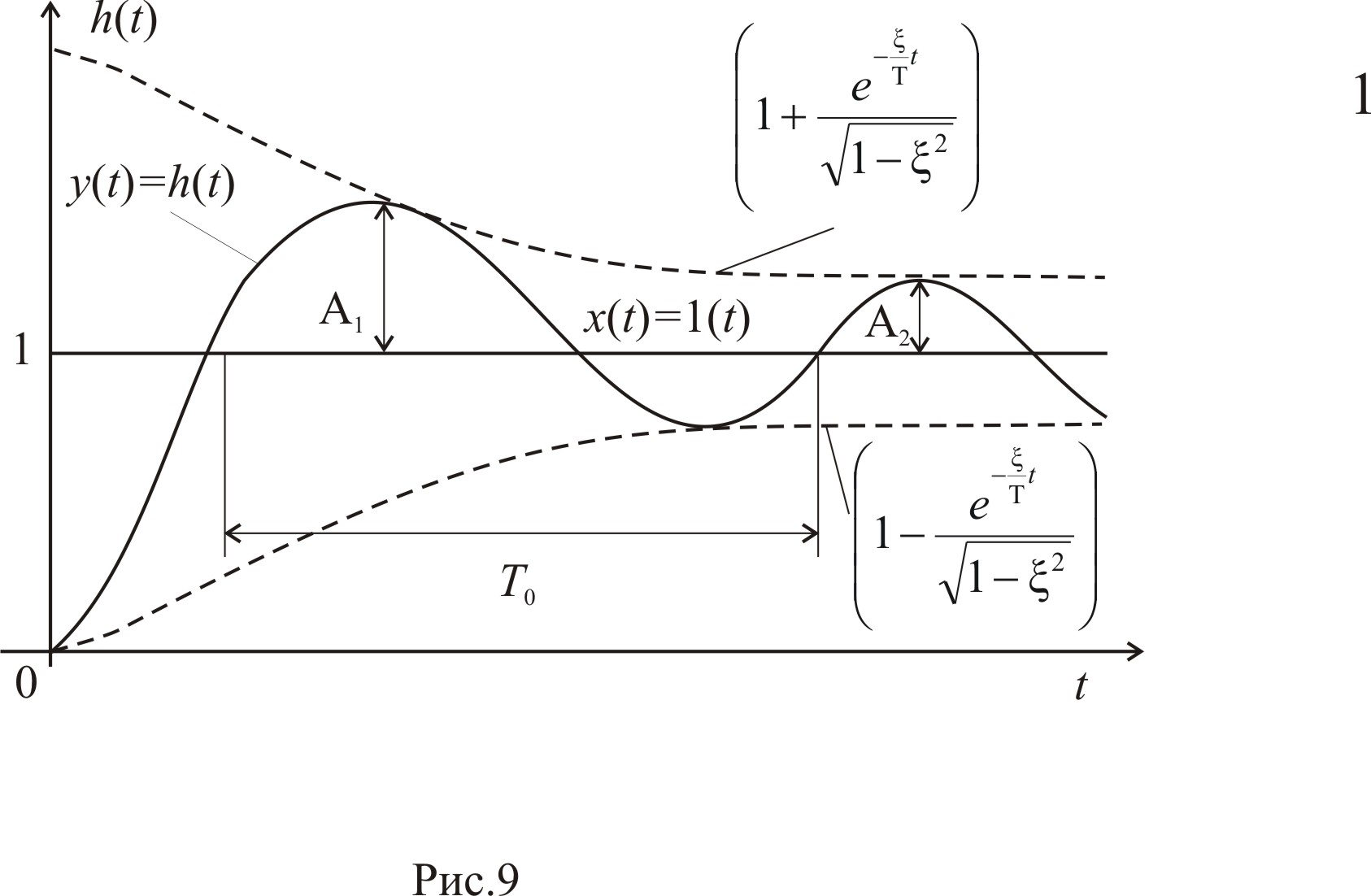
Рис. 9. Переходная характеристика колебательного звена.

Для переходной характеристики колебательного звена параметры Т и  вычисляют по формулам (рис.9):

;

(22)

.

(24)

Рассмотрим случай . Передаточная функция (19) может быть представлена как

,

(25)

где

.

В частном случае при .

Звено с передаточной функцией (25) ( ) называется апериодическим звеном второго порядка. Переходная характеристика такого звена имеет вид:

(26)

График переходной характеристики (26) показан на рис.10.

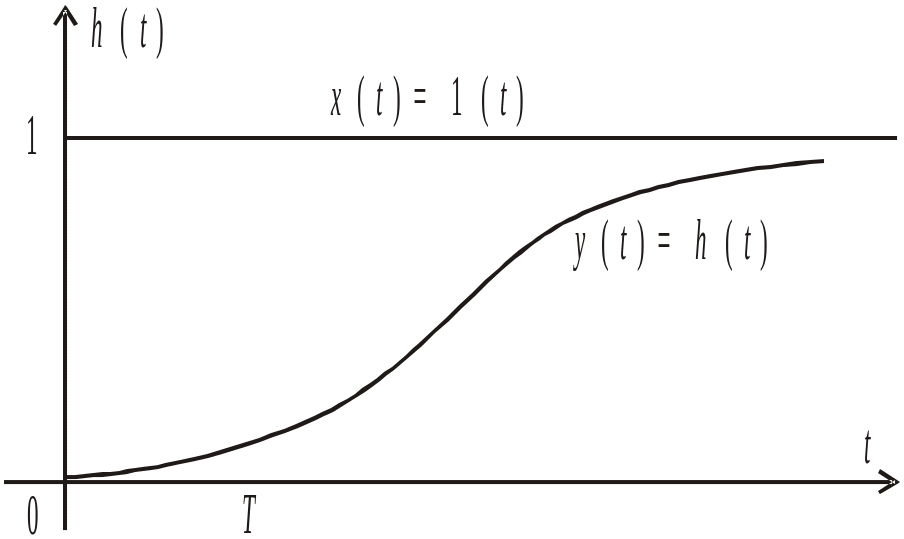
Рис. 10. Переходная характеристика апериодического

звена второго порядка.

Рассмотрим частный случай колебательного звена при .

В этом случае колебательное звено называется консервативным. Его передаточная функция

Переходная характеристика

,

представляет незатухающие гармонические колебания с частотой (рис.11).

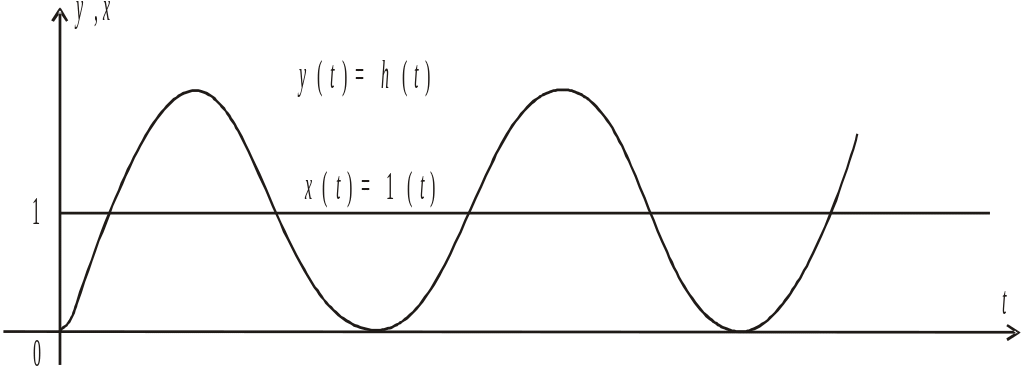
Рис. 11. Переходная характеристика консервативного звена.

На лабораторном стенде колебательное звено реализовано на R,L,C–элементах (рис.12).

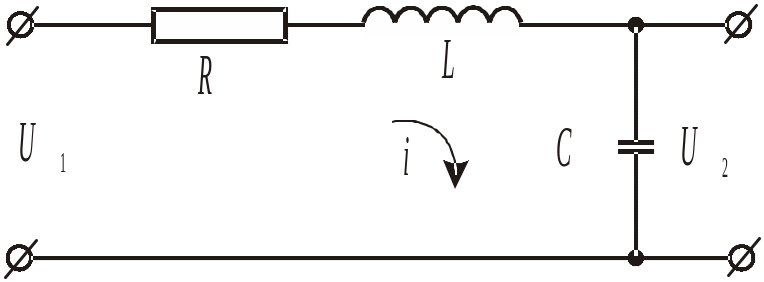
Рис. 12. Колебательное звено на R,L,C–элементах.

Передаточную функцию колебательного звена получим из уравнений:

,

где .

Переходный процесс в цепочке R,L,C (рис.12) будет колебательным при выполнении условия

или

.
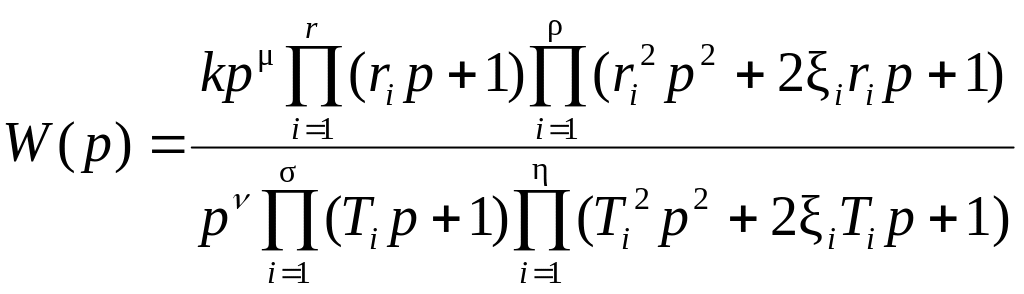