
Нейронные сети (ВМ) / Задания / laba2
.pdf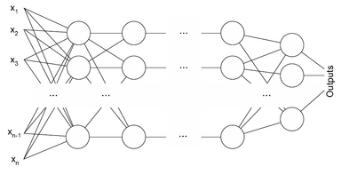
УДК 519.68:007.5
Лабораторная работа 2. Персептрон Румельхарта
Цели работы: реализация персептрона Румельхарта и радиально базисной сети. Анализ возможностей и ограничений метода обратного распространения ошибки.
Ключевые слова: метод обратного распространения ошибки, переобучение сети, паралич коэффициентов.
§1. Обзор теории
1.1.Описание базовых моделей.
Определение 1. Персептрон Румельхарта — это многослойная нейронная сеть, состоящая из однотипных слоев R1, ..., Rn, для которых используются:
• |
|
|
|
|
|
|
|
|
|
σ(x) = 1/(1 + e−x) |
|
|
|
||||
сигмоида в качестве функции активации |
|
ω |
ri j |
x |
ri.j |
(t) |
|
θri j . |
|||||||||
• |
|
r |
i j |
R |
|
значения yri j (t) = σ |
k · |
|
− |
||||||||
для всех нейронов |
|
|
j |
|
x |
ri j |
(t) = yrk j−1 |
|
|
k |
|
|
|||||
• |
сквозное подключение слоев |
|
k |
|
|
P |
|
|
|
|
|
||||||
•общий параметр ν < 1, задающий скорость обучения слоев.
•для выходного слоя Rn оценка ошибки (ei — эталоны для выходов):
δri n (t) = yri n (t)(1 − yri n (t))(yri n (t) − ei(t))
•для внутренних слоев Rj (j ̸= n) суммарная оценка ошибки:
δri j (t) = yri j (t)(1 − yri j (t)) Xδrp j+1 (t) ωirp j+1 (t)
p
• общие формулы для коррекции весов и порогов для всех слоев:
ωkri j (t + 1) = ωkri j (t) − ν δri j (t) xrki j (t)
θri j (t + 1) = θri j (t) − ν δri j (t)
Рис. 1. Персептрон Румельхарта общего вида.

2
Определение 2. Сетью радиально базисных функций будем называть двухслойную нейронную сеть, в которой для нейронов первого слоя используется:
|
|
|
|
|
|
|
|
|
|
|
• Функция агрегации ψ(xi, ωi) = p |
P |
|||||||||
(xki − ωki )2, задающая расстояние от |
||||||||||
входных значений |
xi |
до эталонной точки, представленной весами |
ωi |
. |
||||||
• Функция активации yi(t) = ϕ(zi) = e−βizi2 , где zi = ψ(xi, ωi).
Выходной слой сети как правило состоит из одного нейрона с линейной функцией активации и обычным суммирование в качестве функции агрегации:
X
y(t) = ωk · xk(t), где xk(t) = yk(t).
Обучение сети производится методом обратного распространения ошибки:
ωk(t + 1) = ωk(t) − ν (y(t) − e(t)) xk(t)
|
βk(t + 1) = βk(t) + ν (y(t) − e(t)) xk(t) ωk(t) βk(t) |
|
|||||||||||
ωi |
(t + 1) = ωi |
|
− |
|
− |
|
|
|
|
|
xki − ωki |
|
|
(t) |
ν (y |
e) x ω |
2 β |
ln(1/x ) |
|||||||||
zi |
|||||||||||||
k |
k |
|
|
i i |
p i |
i |
|||||||
1.2. Градиентный спуск с переменным шагом.
Определение 3. Градиентный спуск momentum использует схему вида: v(t + 1) = γ v(t) + ν Jθ(t), θ(t + 1) = θ(t) − v(t + 1)
В этом выражении Jθ задает градиент для оптимизируемого параметра θ, а параметр инерционности устанавливается в γ 0.9.
Определение 4. Ускоренный спуск Нестерова использует схему вида: v(t + 1) = γ v(t) + ν Jθ(t)−v(t), θ(t + 1) = θ(t) − v(t + 1)
Также как и для метода momentum параметр инерционности будет γ 0.9.
Определение 5. Метод Adagrad использует схему вида:
X |
|
|
ν |
|
|
|
|
|
|
Jθ(τ), θ(t + 1) = θ(t) − |
p |
|
· Jθ(t) |
|
Gθ(t) = |
Gθ(t) + ϵ |
|||
τ t |
|
|
|
|
В этом выражении суммирование проводится по всем вычисленным ранее значениям градиентов для параметра θ, а параметр ϵ 10−8 вводится для предотвращения деления на ноль.
Определение 6. Метод Adam использует схему вида:
2
m(t + 1) = β1m(t) + (1 − β1) Jθ(t), v(t + 1) = β2v(t) + (1 − β2) Jθ(t)
mˆ (t) = |
|
m(t) |
, vˆ(t) = |
|
|
v(t) |
, θ(t + 1) = θ(t) − |
|
ν |
|
|
· mˆ (t + 1) |
||
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
βt |
1 |
βt |
|
|
|
|||||||
|
pvˆ(t + |
1) + ϵ |
||||||||||||
|
|
|
− |
1 |
|
|
|
− 2 |
|
8 |
. |
|
||
Значения по умолчанию для β1 0.9 и β2 0.999, а ϵ 10− |
|
|||||||||||||
ЛАБОРАТОРНАЯ РАБОТА 2. ПЕРСЕПТРОН РУМЕЛЬХАРТА |
3 |
§ 2. Практические задания
Задание № 1: Классификация цифр.
1.Реализовать персептрон Румельхарта, для аналогичного задания из лабораторной 1.
2.Имеет ли значение в каком порядке подавать примеры для обучения нашему персептрону?
3.Что представляет из себя эффект паралича коэффициентов сети? Проиллюстрируйте это на примере, поясните механизм возникновения.
4.Реализуйте альтернативные методы стохастического градиентного спуска для данного примера и сравните их скорости сходимости.
5.Что представляет из себя эффект переобучения сети? Поясните на конкретном примере, постаравшись добиться переобучения данной модели, увеличивая число промежуточных слоев.
Задание № 2: Апроксимация хаотических последовательностей.
1.В соотвествии с вариантом выбрать последовательность для апроксимации.
•Вариант 1: x(t + 1) = x(t)(1 − 2(x(t))).
•Вариант 2: x(t + 1) = 4x(t)(1 − x(t)).
•Вариант 3: x(t + 1) = x(t)(1 − x(t)2).
2.Реализовать радиально базисную сеть для предсказания членов последовательности.
3.Проверить, может ли обученная сеть распознавать и предсказывать новые члены за пределами обучающей выборки.
4.Реализуйте альтернативные методы стохастического градиентного спуска для данного примера и сравните их скорости сходимости.
5.Возможны ли в данной моделе паралич коэффициентов или переобучение? Если да, то как бы они себя проявили?
Список литературы
[1]J. Moody, C. J. Darken, “Fast learning in networks of locally tuned processing units”, Neural Computation, 1:2 (1989), 281–294.
[2]Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J., “Learning representations by back-propagating errors”, Nature, 6088:323 (1986), 533–536.
