
Нейронные сети (ВМ) / Задания / laba1
.pdf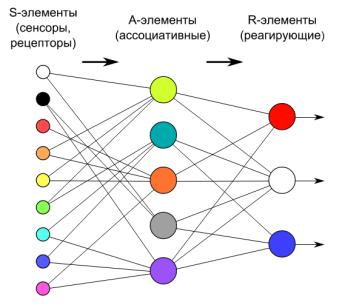
УДК 519.68:007.5
Лабораторная работа 1. Персептрон Розенблатта
Цели работы: решение задач аппроксимации и классификации с помощью модели персептрона. Вычисление A-матрицы и G-матрицы персептрона, анализ скорости сходимости обучения.
Ключевые слова: обучение по Хеббу, метод коррекции ошибки, однослойный персептрон, позиционное и конфигурационное кодирование.
§ 1. Обзор теории
1.1.
Определение 1. Персептрон — это нейронная сеть, состоящая из трех слоев: S = {si} (сенсорный), A = {ai} (ассоциативный), R = {ri} (реагирующий).
•Сенсорные нейроны si S имеют один вход xsi (t) и работают по стандартному правилу ysi (t) = σ(xsi (t) − θsi ), где σ — функция Хевисайда.
•Ассоциативные нейроны ai S подключаются к нескольким нейронам
из S слоя xaj i (t) = ysk (t), используя статические веса ωjai {−1, 0, 1}. Работают ai по аналогичному алгоритму: yai (t) = σ(Pωjai xaj i (t) − θai ).
•Реагирующие нейроны ri R подключаются к нескольким нейронам из A слоя и работают практически также как они за тем исключением, что для них допускаются любые значения для динамических весов ωjri (t).
Рис. 1. Персептрон Розенблатта общего вида.
2
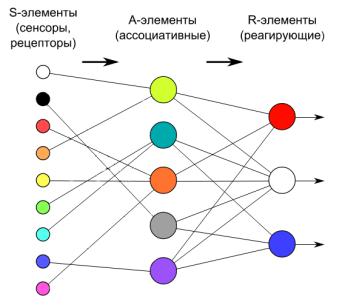
Определение 2. Однослойный персептрон — это частный случай персептрона, для которого каждый s нейрон подключается не более чем к одному a нейрону. Все веса его ассоциативных нейронов ωjai = 1 и пороги θai = 1.
Рис. 2. Однослойный персептрон.
1.2.
Определение 3. Пусть наша нейронная сеть должна обучиться распознавать k различных классов объектов. Тогда, будем называть эталонными стимулами такой набор векторов St1, . . . , Stk, который задает эталонные объекты для этих классов, но преобразованные к формату ввода нашей нейронной сети.
Замечание 1. Розенблаттом было показано, что для решения задачи на классификацию с k различными классами персептрону необходимо как минимум k нейронов в ассоциативном слое.
Определение 4. Назовем [A]-матрицей персептрона такую матрицу, которая задает реакции ассоциативных нейронов aj на эталонные стимулы Sti:
[A]i j = |
(0 |
в противномj |
случае.k |
i |
|
|
|
1, |
если ya (t) = 1 при xs |
(t) = Stk ( |
|
k), |
|
Определение 5. Назовем [G]-матрицей персептрона такую матрицу, которая равна [G] = [A] · [A]T , где T — это операция транспонирования.
Замечание 2. Розенблаттом было показано, что для успешного обучения персептрона на классификацию с k различными классами будет необходимо и достаточно чтобы матрица [G] была не вырожденной (det([G]) ̸= 0).

ЛАБОРАТОРНАЯ РАБОТА 1. ПЕРСЕПТРОН РОЗЕНБЛАТТА |
3 |
1.3.
Определение 6. Будем говорить, что персептрон решает задачу о классификации с помощью позиционного кодирования, если каждый класс i кодируется ровно одним реагирующим1 нейроном ri(t) = 1.
Определение 7. Будем говорить, что персептрон решает задачу о классификации с помощью конфигурационного кодирования, если каждый класс i кодируется бинарным кодом числа i, сформированным выходами слоя R.
Алгоритм обучения персептрона.
Шаг 1: Случайным образом выбираем пороги θai для A нейронов и устанавливаем связи между S и A слоями так, чтобы матрица [G] получилась не вырожденной.
Шаг 2: Начальные коэффициенты R-слоя ωjri полагаем ωjri (0) = 0, а пороги θri устанавливаем в произвольные натуральные значения.
Шаг 3: Выбираем способ кодирования классов для персептрона: конфигурационное или позиционное кодирование (или используем свою схему).
Шаг 4: Подаем в цикле эталонные стимулы Sti на входы персептрона. Проверяем реакции каждого реагирующего нейрона rj нашей схеме кодирования.
•Если выходной нейрон rj был активен yrj (t) = 1, а по нашей схеме он
не должен реагировать на эталонный стимул Sti, то мы уменьшаем все коэффициенты ωkrj (t + 1) = ωkrj (t) − 1, для которых xrkj (t) = 1.
•Если выходной нейрон rj был пассивен yrj (t) = 0, а по нашей схеме он
должен был среагировать на эталонный стимул Sti, то мы увеличиваем все коэффициенты ωkrj (t + 1) = ωkrj (t) + 1, для которых xrkj (t) = 1.
•Если нейрон среагировал на эталонный стимул Sti верно, то мы не изменяем его коэффициенты.
Шаг 5: Повторно проверяем реакцию сети на все эталонные стимулы Sti, но уже без изменения весовых коэффициентов. Если распознание прошло без ошибок, то завершаем работу алгоритма, а иначе возвращаемся к шагу 4.
§ 2. Практические задания
Задание № 1: Классификация цифр.
1.Реализовать персептрон для распознания цифр, заданных на рис. 3.
2.Реализовать однослойный персептрон для этой же задачи.
Рис. 3. Схема кодирования цифр для входов персептрона.
3.Сравнить скорость сходимости для двух моделей персептронов, меняя порядок подачи эталонных стимулов и способ кодирования классов.
4.Проверить работу обеих моделей на искаженных цифрах.
1 Остальные при этом должны быть неактивными rj (t) = 0 j ̸= i.
4
Задание № 2: Классификация букв.
1.Разработать общую схему для кодирования букв русского алфавита.
2.В соотвествии с вариантом выбрать подмножество букв для анализа.
•Вариант 1: Первые 10 букв алфавита.
•Вариант 2: Буквы с 11 по 20.
•Вариант 3: Буквы с 21 по 30.
3.Провести анализ скорости сходимости персептронов для различных вариантов матриц [A] и [G]. Проверять как скорость обучения, так и качество обобщения персептрона (распознание искаженных букв).
4.Будет ли набор собственных чисел матриц влиять на скорость сходимости? Что будет, если все собственные числа отрицательные (или все положительные)? Что будет, если есть совпадающие собственные чила?
Задание № 3: Общая задача на классификацию.
1.Ввести поле из 30 на 30 клеток.
2.Разбить его на 5 непересекающихся областей и выбрать для каждой области несколько эталонных представителей.
3.Построить персептрон, который проводит классификацию в соответсвии с выбранным разбиением.
4.Можно ли эту задачу решать с помощью однослойного персептрона? Получится ли её решить, если области будут не односвязными?
Список литературы
[1]Rosenblatt, Frank, “The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain”, Psychological Review, 65:6 (1958), 386–408.
[2]Rosenblatt, Frank, Principles of Neurodynamics, Washington, 1962.
