физика лаб / 2сем / 9491_Ярошук_Влад_ЛР3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра физики

отчет

по лабораторной работе №3

по дисциплине «Физика»

Тема: Исследование интегральных характеристик электростатического поля методом моделирования (поток электрической индукции)

Студент гр. 9491		Ярошук В. А.
Преподаватель		Миронова Д. В.

Санкт-Петербург

2020

Цели работы: ознакомление с методикой моделирования электростатического поля в токопроводящей среде; исследование электростатического поля, созданного системой проводящих тел; исследование интегральных характеристик электростатического поля – поток вектора напряженности и индукции, теорема Гаусса, циркуляция вектора напряженности.

Исследуемые закономерности: Модель электростатического поля. В проводящей среде под действием приложенной к электродам постоянной разности потенциалов происходит направленное движение заряженных частиц, в результате которого в среде, окружающей электроды, устанавливается стационарное распределение потенциала, подобное распределению потенциала в диэлектрической среде вокруг заряженных проводящих тел, если форма и взаимное расположение последних аналогичны соответствующим параметрам электродов проводящей модели. Сопоставление свойств электростатического поля и поля электрического тока в проводящей среде показывает, что если в электростатическом поле на помещенный в поле заряд действует сила , где n – единичный вектор в направлении максимального изменения потенциала, то в проводящей среде вектор плотности тока подчиняется вполне симметричному соотношению , где  – электропроводность среды (величина, обратная удельному сопротивлению). Из сопоставления двух соотношений видно, что, во-первых, оба поля потенциальны, (не образуют вихрей в пространстве, окружающем электроды), а во-вторых, как линии напряженности электростатического поля, так и линии тока перпендикулярны линиям или поверхностям равного потенциала.

Поле длинной двухпроводной линии. На планшете моделируются так называемые плоские поля, т. е. поля, картина которых остается неизменной при параллельном переносе плоскости, в которой производится исследование поля. Обычно, это электростатические поля объектов, бесконечно протяженных в направлении, перпендикулярном секущей плоскости. В работе исследуется поле двух длинных, параллельных, равномерно и разноименно заряженных проводящих цилиндров (двухпроводной линии). Если абсолютное значение линейной плотности заряда на цилиндрах  (Кл/м), то напряженность электростатического поля в произвольной точке секущей плоскости будет определяться геометрической суммой напряженностей полей, создаваемых каждым цилиндром (принцип суперпозиции). Для каждого из цилиндров абсолютное значение напряженности поля , а значение и направление результирующего вектора напряженности поля определяют по отношению к системе координат, заданной экспериментатором.

Напряженность поля и вектор индукции. Для электростатического поля справедливо следующее соотношение между вектором напряженности поля и вектором электрической индукции: . Особенность вектора электрической индукции состоит в том, что, описывая с помощью этой физической величины электрическое поле, исследователь избавляется от необходимости учитывать связанные заряды, возникающие при поляризации среды.

Поток вектора индукции электрического поля (теорема Гаусса). Поток вектора индукции электрического поля определяется выражением S – поверхность произвольной формы в области поля; n – единичный вектор нормали в данной точке поверхности. Поток вектора индукции поля является характеристикой источников этого поля. Для электростатического поля справедлива теорема Гаусса где S – произвольная замкнутая поверхность в области поля; V – объем области поля, ограниченный поверхностью S; QV – заряд, распределенный в объеме V. Выражение означает: поток вектора индукции электростатического поля через замкнутую поверхность произвольной формы равен суммарному заряду, заключенному в объеме, ограниченном этой поверхностью, и не зависит от зарядов, расположенных вне данной поверхности.

Протокол к лабораторной работе №3

	X1, см/ Y1, см / Ф1, В	X2, см/ Y2, см / Ф2, В
	x=3.99cm y=11.12cm φ = 13.6 B	x=27.9cm y=11.12cm φ = 0.38 B
	x=3.99cm y=11.62cm φ = 13.28 B	x=28.43cm y=11.02cm φ = 0.32 B
	x=4.46cm y=11.55cm φ = 13.2 B	x=28.96cm y=10.7cm φ = 0.24 B
	x=4.46cm y=11.04cm φ = 13.54 B	x=29.38cm y=10.28cm φ = 0.21 B
	x=4.99cm y=11.28cm φ = 13.15 B	x=29.67cm y=9.64cm φ = 0.19 B
	x=4.99cm y=10.75cm φ = 13.51 B	x=29.7cm y=9.01cm φ = 0.18 B
	x=5.49cm y=11.02cm φ = 13.01 B	x=29.54cm y=8.43cm φ = 0.19 B
	x=5.36cm y=10.36cm φ = 13.5 B	x=29.25cm y=7.88cm φ = 0.26 B
	x=5.62cm y=9.86cm φ = 13.49 B	x=28.8cm y=7.53cm φ = 0.3 B
	x=5.83cm y=9.33cm φ = 13.36 B	x=28.35cm y=7.35cm φ = 0.34 B
	x=5.73cm y=8.77cm φ = 13.44 B	x=27.9cm y=7.22cm φ = 0.44 B
	x=5.49cm y=8.14cm φ = 13.42 B	x=27.22cm y=7.37cm φ = 0.48 B
	x=5.12cm y=7.77cm φ = 13.49 B	x=26.72cm y=7.72cm φ = 0.47 B
	x=4.62cm y=7.48cm φ = 13.56 B	x=26.27cm y=8.17cm φ = 0.54 B
	x=4.12cm y=7.29cm φ = 13.57 B	x=26.03cm y=8.69cm φ = 0.54 B
	x=3.56cm y=7.29cm φ = 13.62 B	x=25.92cm y=9.17cm φ = 0.6 B
	x=2.93cm y=7.56cm φ = 13.72 B	x=26cm y=9.75cm φ = 0.59 B
	x=2.38cm y=8.03cm φ = 13.76 B	x=26.19cm y=10.17cm φ = 0.57 B
	x=2.06cm y=8.64cm φ = 13.79 B	x=26.43cm y=10.54cm φ = 0.57 B
	x=1.9cm y=9.2cm φ = 13.77 B	x=26.85cm y=10.81cm φ = 0.46 B
	x=1.98cm y=9.72cm φ = 13.77 B	x=27.38cm y=11.12cm φ = 0.48 B
	x=2.14cm y=10.17cm φ = 13.74 B	x=27.9cm y=11.65cm φ = 0.71 B
	x=2.51cm y=10.59cm φ = 13.73 B	x=28.56cm y=11.55cm φ = 0.61 B
	x=2.98cm y=10.91cm φ = 13.7 B	x=29.33cm y=11.12cm φ = 0.5 B
	x=3.43cm y=11.07cm φ = 13.66 B	x=29.81cm y=10.54cm φ = 0.41 B
	x=5.78cm y=10.59cm φ = 13.01 B	x=30.18cm y=9.64cm φ = 0.37 B
	x=6.05cm y=10.07cm φ = 12.98 B	x=30.2cm y=9.04cm φ = 0.37 B
	x=6.26cm y=9.43cm φ = 12.89 B	x=30.04cm y=8.17cm φ = 0.42 B
	x=6.26cm y=8.67cm φ = 12.85 B	x=29.7cm y=7.53cm φ = 0.49 B
	x=5.94cm y=8.09cm φ = 12.98 B	x=29.07cm y=7.03cm φ = 0.57 B
	x=5.54cm y=7.48cm φ = 13.01 B	x=28.46cm y=6.9cm φ = 0.6 B
	x=5.02cm y=7.03cm φ = 13.07 B	x=27.9cm y=6.69cm φ = 0.76 B
	x=4.36cm y=6.87cm φ = 13.23 B	x=26.82cm y=6.93cm φ = 0.94 B
	x=3.51cm y=6.69cm φ = 13.28 B	x=26.35cm y=7.37cm φ = 0.94 B
	x=2.38cm y=7cm φ = 13.39 B	x=25.71cm y=7.88cm φ = 1.16 B
	x=1.69cm y=7.74cm φ = 13.49 B	x=25.45cm y=8.61cm φ = 1.18 B
	x=1.37cm y=8.59cm φ = 13.55 B	x=25.45cm y=9.12cm φ = 1.13 B
	x=1.27cm y=9.12cm φ = 13.55 B	x=25.53cm y=9.93cm φ = 1.13 B
	x=1.4cm y=9.86cm φ = 13.55 B	x=25.79cm y=10.52cm φ = 1.08 B
	x=1.61cm y=10.49cm φ = 13.51 B	x=26.22cm y=10.99cm φ = 0.99 B
	x=2.24cm y=11.07cm φ = 13.49 B	x=26.72cm y=11.28cm φ = 0.86 B
	x=2.82cm y=11.49cm φ = 13.4 B	x=27.32cm y=11.57cm φ = 0.79 B

x=9.98cm y=7.98cm φ = 10.19 B

x=10.51cm y=7.98cm φ = 9.99 B

x=9.98cm y=7.48cm φ = 10.16 B

72 В/м

126 В/м

42 В/м

0,33 ± 0,07 Кл/м²

-37,7 В/м

-6 В/м

74 В/м

94 В/м

В ходе данной лабораторной работы был использован метод моделирования электростатического поля. Также были рассчитаны потоки вектора индукции _{, .} Были найдены погонные заряды цилиндров 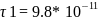, Кл/м. < _, что подтверждает теорему Гаусса экспериментально.