физика лаб / 2сем / 13

1 Сформулируйте закон Био-Савара-Лапласа.

Закон Био—Савара—Лапласа — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).

Если же взять за точку отсчёта точку, в которой нужно найти вектор магнитной индукции, то формула немного упрощается:

где  - вектор описывающий кривую проводника с током  ,  - модуль  ,  - вектор магнитной индукции, создаваемый элементом проводника

2. Вы ведите из основной формулы закона БСЛ (формула 1 у вас в теории) выражение для индукции магнитного поля на оси кругового тока (формула 2 у вас в теории). Почему у магнитной индукции есть только составляющая по оси у, и нет составляющей по оси х?

Рассмотрим проводник с током, имеющий форму окружности радиуса R , Определим магнитную индукцию в его центре.

Каждый элемент тока  создает магнитное поле индукцией , перпендикулярное к плоскости витка.

Все вектора направлены одинаково, поэтому их векторное сложение сведется к сложению их модулей. Тогда

.

Так как  , то для магнитной индукции в центре кругового тока получаем:

y

О пределим магнитную индукцию в любой точке на оси кругового тока. Обозначим y расстояние от плоскости контура до некоторой точки на оси (рис.4.6).

Так как вектор  , то модуль вектора равен:

. (1)

Вектор  перпендикулярен плоскостям, проходящим через и r. От всех элементов тока будет образовываться «конус» векторов .

Разложим вектор  на две составляющие: перпендикулярную и параллельную оси: . Применим принцип суперпозиции полей, получим:

Нетрудно убедиться, что векторная сумма всех перпендикулярных составляющих равна нулю, и результирующий вектор  будет направлен вдоль оси тока. Вклад в него будут вносить только параллельные оси составляющие векторов . Тогда

Из треугольника (см. рис.4.6) следует:

. (2)

Подставим выражение (1) в формулу (2), получим:

Возьмём интеграл:  , получим:

,

Или  

Так как 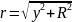 , то окончательно получим:

X

Y

B_x = 0

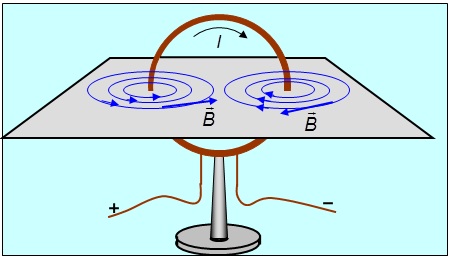
3. Круговой ток, изобразите качественно линии индукции кругового тока.

Круговой ток - ток текущий по тонкому круглому проводу.

Линии магнитной индукции для кругового тока представляют собой замкнутые окружности, а внутри соленоида – ряд линий, параллельных оси соленоида.

4. Магнитный момент кругового тока и его физический смысл.

Магнитный момент кругового контура с током Pm равен:

Pm = ISn. где I{\displaystyle I} — сила тока в контуре, {\displaystyle S} — S площадь контура, {\displaystyle \mathbf {n} } — n единичный вектор нормали к плоскости контура. 

Магни́тный моме́нт— основная величина, характеризующая магнитные свойства вещества (источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки; элементарным источником магнетизма считают замкнутый ток). Магнитными свойствами обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других частиц), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина.

Магнитный момент измеряется в А⋅м² , или в Вб*м, или Дж/Тл

5. В чем заключается явление электромагнитной индукции?

Явление электромагнитной индукции заключается в возникновении электрического тока в замкнутом проводнике при изменении магнитного потока, пронизывающего охваченную проводником площадь.