МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра физики

ОТЧЕТ

по лабораторной работе №15

Тема:Моделирование магнитного поля токов

Студент гр. 9491		Богомолова М.В.
Преподаватель		Мыльников И.Л.

Вопросы:

20. Какова траектория движения заряженной частицы, влетающей в магнитное поле перпендикулярно линиям индукции? Ответ обоснуйте.

Если заряженная частица влетает в магнитное поле перпендикулярно линиям индукции магнитного поля, т.е. 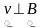, то она начинает двигаться по окружности постоянного радиуса с постоянной по модулю скоростью

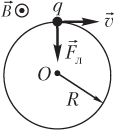
Равнодействующая сил, действующих на частицу, при движении по окружности является центростремительной силой. Сила Лоренца в данном случае является единственной силой (следовательно, она равна центростремительной силе), поэтому справедлива следующая система уравнений:

F_л=qvB

F_ц.с=F_л

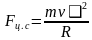
где q — величина заряда частицы; v — модуль скорости частицы; B — модуль индукции магнитного поля; m — масса заряженной частицы; R — радиус окружности, по которой движется частица.

25. В чем заключается эффект Холла?

При помещении в магнитное поле пластины-проводника или полупроводника под 90 °к направлению силовых линий магнитного потока произойдет перемещение электронов по поперечине пластины под действием силы Лоренца. Их направление зависит от того, в какую сторону идет сила тока и силовые линии магнитного потока. Иначе говоря, (ЭХ) эффект Холла – это частный случай действия силы Лоренца, то есть действия магнитного поля на заряженную частицу.

Если представить расположенную к нам торцом пластину, то ее кромка направлена вниз. Она сделана из металла, оба торца подключены к источнику питания, задний из которых на минус, передний на плюс.

Данный случай говорит о том, что электрический ток будет протекать по направлению к наблюдателю. Справа и слева от пластины располагаются два магнита. Правый из них обращен к пластине северным полюсом, левый – южным. Делаем вывод, что данный случай показывает направление силовых линий магнитного поля справа налево, так как они всегда выходят из северного полюса и входят в южный. Силовые линии отклоняют электроны, которые проходят по пластине к ее верхней кромке.

При изменении направления тока в пластине при помощи перемены местами проводников мы сможем наблюдать отклонение электронов вниз. Если направление не менять, а только лишь полюса магнитов, электроны начнут сдвигаться вниз. Когда применяются оба направления, сила Лоренца произведет их перемещение вверх.

Очевидно, что одна из кромок накапливает отрицательный заряд под действием силы Лоренца, на другая на противоположной стороне – положительный. Это говорит о наличии разности потенциалов между ними, то есть электрического напряжения. Увеличение этой разности будет происходить до тех пор, пока не уравновесит силу Лоренца.

Цель работы: изучение магнитного поля системы проводников с использованием графической карты поля, полученной методом моделирования; расчет индуктивности системы проводников заданной конфигурации.

Приборы и принадлежности: измерительная схема; пантограф с зондом.

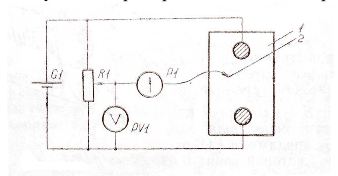
Основные теоретические положения:

Электрическое и магнитное поля неразрывно связаны между собой, образуя электромагнитное поле. Так, электрический заряд, создающий электростатическое поле в системе отсчета (СО), относительно которой он покоится, создает магнитное поле в СО, относительно которой происходит движение заряда.

Рассмотрим СО, равномерно движущуюся со скоростью V параллельно проводнику, заряженному с линейной плотностью заряда τ . Для наблюдателя, находящегося в этой СО, проводник движется со скоростью -V, создавая ток:

I = –τV

(в СО наблюдателя)

и магнитное поле, индукция которого равна

B = –μμ₀εε₀V×E

где μ₀ и ε₀ – магнитная и электрическая постоянные; μ и ε – относительные магнитная и диэлектрическая проницаемости среды; Е – напряженность электростатического поля, создаваемого зарядами, в СО, относительно которой они покоятся.

Вектор В направлен по касательной к эквипотенциальной линии исходного электростатического поля, а его модуль равен

B = μμ₀εε₀v(dφ/dr). (1)

Здесь учтена связь напряженности E и потенциала φ электрического поля:

E = –grad φ = –(dφ/dr)r₀,

где r0 – единичный вектор (орт) в направлении, перпендикулярном к эквипотенциальной линии.

Таким образом, получить графическое представление магнитного поля системы проводников с токами можно на карте электростатического поля, создаваемого такими же заряженными проводниками.

Чтобы полученную карту эквипотенциалей преобразовать в карту магнитного поля конкретных токов следует в выражении (1) задать в явном виде масштабный коэффициент k = εε0V.

Для этого можно воспользоваться законом полного тока

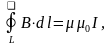
где контур L представляет собой замкнутую линию индукции, охватывающую проводник с током I. Разбиение контура интегрирования на элементы ∆l_i позволяет представить интеграл суммой

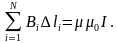(2)

Если контуру L карты магнитного поля сопоставляется ближайшая к электроду эквипотенциаль φ1 то, согласно (1),

B = –μμ₀εε₀v(φ₀ –φ₁)/∆r_i ,

где φ₀ – потенциал электрода. Подстановка этого выражения в (2) дает

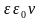(3)

Из этого соотношения и определяется масштабный коэффициент k = εε0V после разбиения контура L на отрезки ∆li и определения суммы

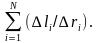
В описанном варианте разбиения контура на отрезки ∆li (возможны и другие варианты) все отношения ∆li/∆ri = 1 и∆li/∆ri) = N, где N—число участков ∆li, получившихся на замкнутой линии. Тогда, согласно (3),

k = 1/(N(φ₀ – φ₁ )) (4)

Зная величину масштабного множителя k, индукцию в любой точке карты магнитного поля можно определить по формуле

Bk = –μμ₀k∆φ_k/∆r_k, (5)

где ∆φk и ∆rk – разность потенциалов и кратчайшее расстояние между ближайшими эквипотенциалями, соответственно, в окрестности рассматриваемой точки .

Графическая карта магнитного поля позволяет вычислить индуктивность моделируемой системы проводников. Индуктивность L определяется как коэффициент пропорциональности между током I и создаваемым им магнитным потоком Ψ.

Ψ = LI. (6)

Для приближенного расчета L необходимо вычислить магнитный поток через поверхность abcd между проводниками. Приближенный расчет данного интеграла можно произвести, разбивая поверхность abcd на элементарные площадки, длина которых равна h, а ширина – расстоянию между соседними линиями индукции ∆r_k .

Тогда Ψ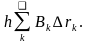

или, с учетом выражения (5),

Ψ = μμ₀hkU. (7) Здесь учтено, что φ_k = U, где U—разность потенциалов между электродами модели.

Сопоставляя выражения (4), (6) и (7), находим индуктивность, приходящуюся на единицу длины проводников (погонную индуктивность)

Lп = L/h = μμ₀kU/I = μμ₀U/(N(φ₀ – φ₁)).

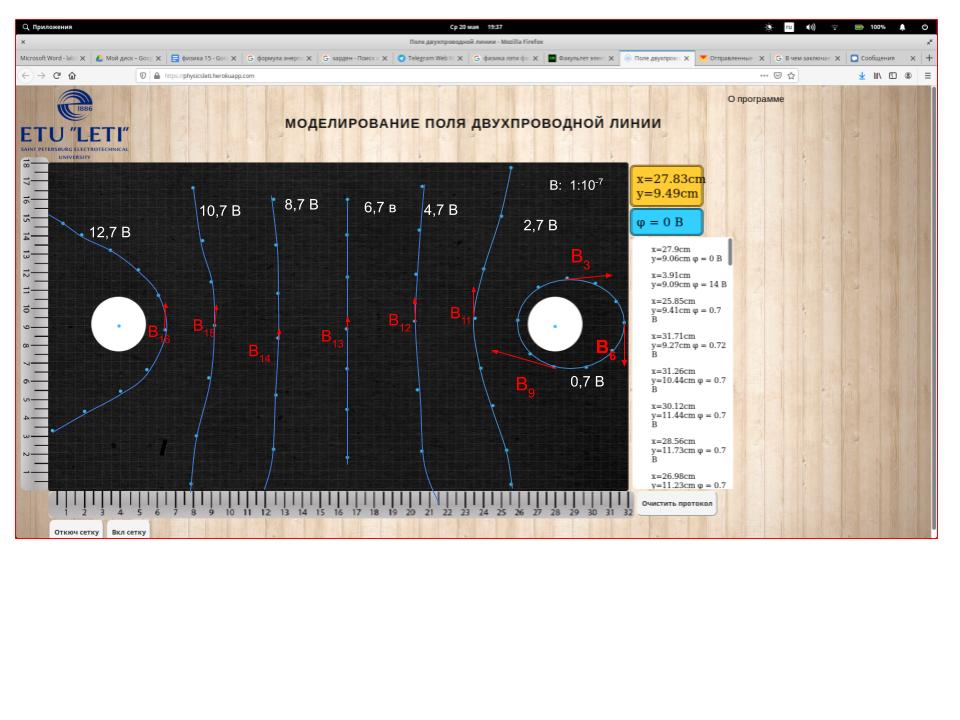
Протокол к лабораторной работе №15

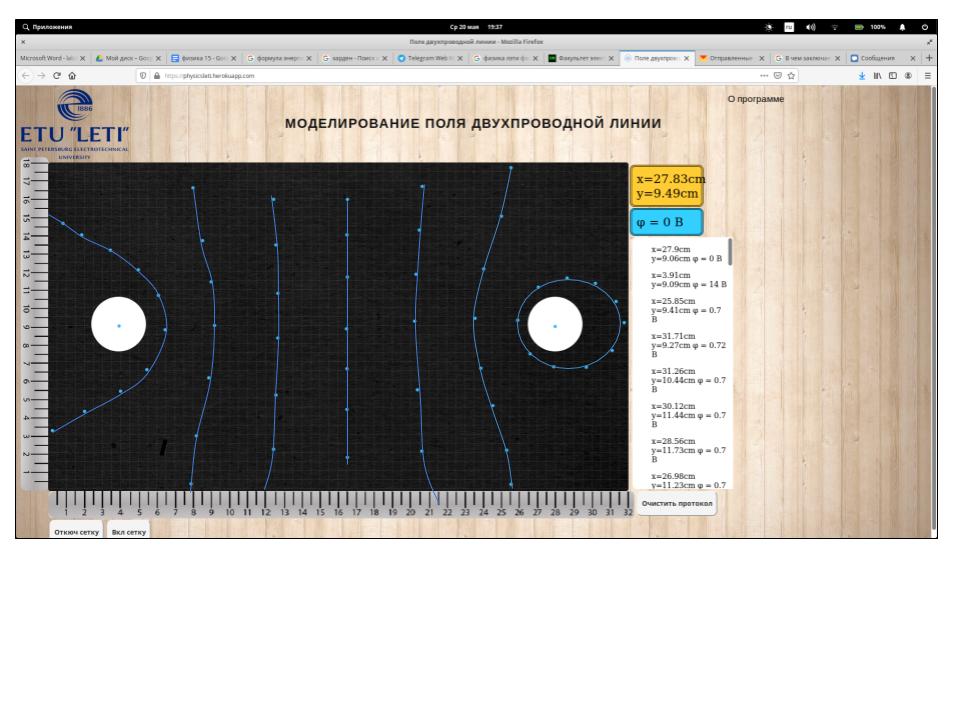
1. Показания вольтметра на электродах:

x=27.9cm y=9.06cm φ = 0 B

x=3.91cm y=9.09cm φ = 14 B

2. показания вольтметра на эквипотенциалях:

x=25.85cm y=9.41cm φ = 0.7 B

x=31.71cm y=9.27cm φ = 0.72 B

x=31.26cm y=10.44cm φ = 0.7 B

x=30.12cm y=11.44cm φ = 0.7 B

x=28.56cm y=11.73cm φ = 0.7 B

x=26.98cm y=11.23cm φ = 0.7 B

x=26.53cm y=7.56cm φ = 0.7 B

x=27.83cm y=6.85cm φ = 0.68 B

x=29.62cm y=6.82cm φ = 0.7 B

x=31.05cm y=7.74cm φ = 0.7 B

x=23.5cm y=9.51cm φ = 2.7 B

x=23.97cm y=12.23cm φ = 2.7 B

x=24.95cm y=15.14cm φ = 2.7 B

x=25.48cm y=17.8cm φ = 2.7 B

x=23.81cm y=6.77cm φ = 2.7 B

x=24.47cm y=4.71cm φ = 2.7 B

x=25.24cm y=2.25cm φ = 2.7 B

x=25.48cm y=0.38cm φ = 2.7 B

x=20.17cm y=9.35cm φ = 4.7 B

x=20.25cm y=11.94cm φ = 4.7 B

x=20.43cm y=14.37cm φ = 4.7 B

x=20.59cm y=16.77cm φ = 4.7 B

x=20.33cm y=5.58cm φ = 4.7 B

x=20.57cm y=2.2cm φ = 4.7 B

x=16.42cm y=8.93cm φ = 6.7 B

x=16.47cm y=11.78cm φ = 6.68 B

x=16.45cm y=14.11cm φ = 6.7 B

x=16.47cm y=16.06cm φ = 6.7 B

x=16.45cm y=6.74cm φ = 6.7 B

x=16.45cm y=4.5cm φ = 6.7 B

x=16.47cm y=1.86cm φ = 6.7 B

x=12.65cm y=8.43cm φ = 8.71 B

x=12.65cm y=10.89cm φ = 8.7 B

x=12.54cm y=13.55cm φ = 8.69 B

x=12.41cm y=16.06cm φ = 8.7 B

x=12.54cm y=5.29cm φ = 8.7 B

x=12.41cm y=2.31cm φ = 8.7 B

x=9.16cm y=9.12cm φ = 10.7 B

x=8.98cm y=11.52cm φ = 10.7 B

x=8.5cm y=13.79cm φ = 10.7 B

x=7.97cm y=16.69cm φ = 10.7 B

x=8.84cm y=6.24cm φ = 10.7 B

x=8.16cm y=3.04cm φ = 10.7 B

x=7.87cm y=0.4cm φ = 10.7 B

x=6.44cm y=8.88cm φ = 12.7 B

x=6.07cm y=10.78cm φ = 12.7 B

x=4.96cm y=12.18cm φ = 12.7 B

x=3.43cm y=13.26cm φ = 12.7 B

x=1.85cm y=14.11cm φ = 12.7 B

x=5.44cm y=6.69cm φ = 12.7 B

x=3.99cm y=5.5cm φ = 12.7 B

x=2.01cm y=4.39cm φ = 12.7 B

x=0.24cm y=3.33cm φ = 12.7 B

x=0.82cm y=14.74cm φ = 12.7 B

Обработка результата эксперемента

1. Перевод графической карты электрического поля в карту магнитного поля.

I=50 мA; μ=1; μ₀=4π • 10^-7

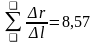
∆r, см	0,5	0,7	1,2	1,7	2,19	2,35	2,01	1,49	0,79	0,69
∆l, см	2,24	1,55	1,64	1,5	1,25	1,67	1,7	1,79	1,48	1,97

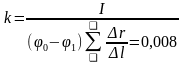
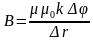
	3	6	9	11	12	13	14	15	16
B, 10-7 Тл	5,88	3,002	8,93	3,002	2,11	1,87	1,85	1,98	2,58

2) Вычисление погонной индуктивности моделируемой системы:

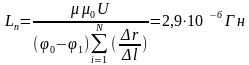
Вывод теоретической:

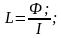dФ= BdS; dS = ldr;

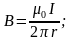
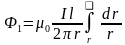; d>>r; Ф=2Ф₁, т.к. поток второго провода такой же.

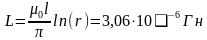
Вывод. Теоретическое и практическое значения погонной индуктивности практически идеально сошлись, а значит метод моделирования магнитного поля был верным.

Санкт-Петербург

2020