физика лаб / экз / мой билет и ост / Лекция1

ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Энергия заряженного проводника.

Для энергии взаимодействия системы зарядов было получено выражение

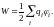(1)

Здесь φ_i ― потенциал, создаваемый всеми зарядами, кроме q_i, в месте расположения заряда q_i.

Заряд q, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов Δq. Поверхность проводника является эквипотенциальной. По формуле (1) получим для энергии заряженного проводника выражение

Можно также написать:

(2)

где С ― ёмкость проводника.

Энергия заряженного конденсатора.

Пусть потенциал обкладки конденсатора, на которой распределён заряд +q, равен φ₁, а потенциал обкладки, на которой распределён заряд –q равен φ₂. Тогда, согласно формуле (2) получаем:

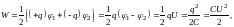(3)

где С ― ёмкость конденсатора, U ― напряжение на конденсаторе.

Энергия электрического поля.

Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле между обкладками конденсатора. Для простоты сделаем это для плоского конденсатора с однородным заполнением, ёмкость которого . Тогда

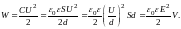(4)

Здесь Е ― напряжённость поля в зазоре, V ― объём, занимаемый полем.

Формула связывает энергию конденсатора с зарядом на его обкладках, формула ― с напряжённостью поля. Вопрос: что является носителем энергии ― заряды или поле? В рамках электростатики, которая изучает постоянные во времени поля неподвижных зарядов дать ответ на этот вопрос невозможно. Постоянные во времени поля и порождающие их заряды не могут существовать обособленно друг от друга. Однако меняющиеся во времени поля могут существовать независимо от возбудивших их зарядов и распространяться в пространстве в виде электромагнитных волн, переносящих энергию. Этот факт заставляет признать, что носителем энергии является поле.

Из (4) следует, что плотность энергии поля напряжённости Е, созданного в среде с проницаемостью ε, равна

(5)

Заменив в (5) 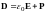, получим

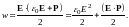(6)

Первое слагаемое в (6) совпадает с плотностью энергии поля Е в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию единицы объёма диэлектрика. Докажем это.

Поляризация диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поля Е. В расчёте на единицу объёма (V = 1) диэлектрика работа, затрачиваемая на смещение зарядов q_i на величину , равна

(для простоты считаем поле однородным), 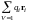равна дипольному моменту единицы объёма, то есть поляризованности диэлектрика Р. Следовательно,

откуда 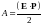. Ч.Т.Д.

_{Заметим, что выражение для плотности энергии электрического поля}

остается справедливым и в общем случае переменных во времени полей.

Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключённую в объёме V:

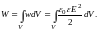(7)

Рассмотрим вопрос о различном содержании уравнений

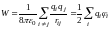(8)

с одной стороны и уравнения (7) с другой стороны. То, что эти уравнения разнятся по своему содержанию, явствуют хотя бы из того обстоятельства, что энергия, определяемая уравнением (7), не может принимать отрицательных значений (ибо Е² > 0), тогда как, согласно (8), энергия взаимодействия точечных зарядов W < 0, если заряды разноимённые. Объясняется это тем, что в уравнениях (8) учитывается лишь взаимодействие ряда «точечных» зарядов, но не взаимодействие отдельных элементов каждого такого заряда между собой. Действительно, если мы имеем дело лишь с одним единственным «точечным» зарядом q₁, то выражения (8) обратятся в 0, тогда как выражение (7) будет иметь отличное от нуля и притом положительное значение, равное так называемой собственной энергии заряда q₁. Собственная энергия заряда зависит, конечно, от его размеров и равна той работе, которую бы совершили силы отталкивания между элементами заряда, если бы эти элементы разлетелись в стороны и удалились в бесконечность.

Рассмотри полную (то есть собственную и взаимную) энергию двух зарядов q₁ и q₂. Пусть каждый из этих зарядов в отдельности возбуждает соответственно поля Е₁ и Е₂, так что результирующее поле Е обоих зарядов равно Е = Е₁ + Е₂ и Полная энергия зарядов q₁ и q₂, согласно (7), будет равна

или 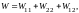где и суть собственные

энергии зарядов q₁ и q₂ соответственно, а есть их взаимная энергия. Из следует, что 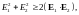так что . Таким образом, положительная собственная энергия зарядов всегда больше (или в крайнем случае равна) их взаимной энергии, могущей иметь как положительные, так и отрицательные значения.

При всех возможных перемещениях зарядов, не изменяющих их формы и размеров, собственная энергия зарядов остаётся постоянной. Поэтому при этих перемещениях члены W₁₁ и W₂₂ можно считать аддитивными постоянными в выражении полной энергии W, изменение которой всецело определяется изменением взаимной энергией зарядов W₁₂. При достаточно больших расстояниях между зарядами выражение сводится к выражению . (Докажите самостоятельно.)

Чрезвычайно важно отметить, что энергия электрического поля не обладает свойством аддитивности, то есть, что энергия поля Е являющаяся суммой двух полей Е₁ и Е₂, вообще говоря, не равна сумме энергий слагаемых полей (если только W₁₂ не равна нулю). В частности, при возрастании напряжённости поля в n раз, энергия поля возрастает в n² раз.

Пример. Вычислим энергию поля заряженного (q) проводящего шара радиуса R, помещённого в однородный безграничный диэлектрик (ε).

Разобьём окружающее шар пространство на концентрические шаровые слои толщиной dr. Объём слоя 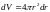. В нём заключена энергия

Энергия поля равна 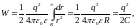что совпадает с выражением для энергии проводника, обладающего ёмкостью С и несущего на себе заряд q.