физика лаб / экз / мой билет и ост / Магнетизм_3

Магнитное поле в веществе

Намагничение магнетика

Всякое вещество является магнетиком, т. е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создаёт магнитное поле В´, которое накладывается на обусловленное токами поле В₀. Оба поля дают в сумме результирующее поле

В = В₀ + В´. (3.1)

Истинное (микроскопическое) поле в магнетике сильно изменяется в пределах межмолекулярных расстояний. Под В понимается усреднённое (макроскопическое) поле.

Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные токи). Каждый такой ток обладает магнитным моментом и создаёт в окружающем пространстве магнитное поле. В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего обусловленное ими результирующее поле равно нулю. В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю. Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается ― его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле В´.

Намагничение магнетика естественно характеризовать магнитным моментом единицы объёма. Эту величину называют намагниченностью и обозначают буквой J. Если магнетик намагничен неоднородно, намагниченность в данной точке определяется следующим выражением:

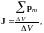(3.2)

где ∆V ― физически бесконечно малый объём, взятый в окрестности рассматриваемой точки, p_m ― магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заключённым в объёме ∆V.

Поле В´, так же как и поле В₀ не имеет источников. Поэтому дивергенция результирующего поля (3.1) равно нулю:

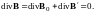(3.3)

Таким образом, формула (2.21), а следовательно, и формула (2.20) справедливы не только в вакууме, но и для поля в веществе.

Напряжённость магнитного поля

Напишем выражение для ротора результирующего поля (3.1):

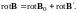
Согласно (2.26) rotB₀ = μ₀j, где j ― плотность макроскопического тока. Аналогично ротор вектора В´ должен быть пропорционален плотности молекулярных токов:

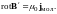
Следовательно, ротор результирующего поля определяется формулой

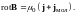(3.4)

Для того, чтобы определить rotB нужно знать плотность не только макроскопических, но также и молекулярных токов. Плотность же молекулярных токов в свою очередь зависит от значения вектора В. Оказывается, можно найти такую вспомогательную величину, ротор которой определяется лишь плотностью макроскопических токов.

Молекулярные токи (токи намагничения) ― постоянные микроскопические токи, не поддающиеся макроскопическому наблюдению. Из-за неполной компенсации этих токов в атомном масштабе могут возникнуть суммарные поверхностные или объёмные токи. Плотность токов намагничения j_мол может быть выражена через намагниченность магнетика J:

j_мол = rotJ. (3.5)

Физический смысл соотношения (3.5) можно понять следующим образом. Рассмотрим z-компоненты магнитных моментов двух контуров с током, расположенных в плоскости xy прямоугольной системы координат (рис. 3. 1). В первом контуре течёт ток

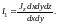
Ток во втором контуре нетрудно оценить, пользуясь разложением в ряд Тейлора:

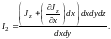
Разность между I₁ и I₂ даёт ток в направлении оси y вдоль общей границы обоих контуров:

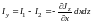
и для плотности тока в направлении оси y получаем:

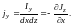
Как нетрудно видеть, эта разность представляет собой одну из шести компонент ротора, то есть в общем случае

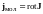(3.5)

Подставим найденное выражение для плотности молекулярных токов в формулу (3.4):

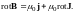
Разделив это соотношение на μ₀ и объединив вместе роторы, получим

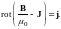(3.6)

Отсюда следует, что

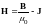(3.7)

есть искомая вспомогательная величина, ротор которой определяется одними лишь макроскопическими токами. Это величина называется напряжённостью магнитного поля.

В соответствии с (3.6)

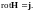(3.8)

Возьмём произвольный контур L с натянутой на него поверхностью S и образуем выражение

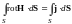
Согласно теореме Стокса левая часть этого равенства эквивалентна циркуляции вектора Н по контуру L. Следовательно,

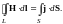(3.9)

Если макроскопические токи текут по проводам, охватываемым контуром, соотношение (3.9) можно записать в виде

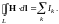(3.10)

Формулы (3.9) и (3.10) выражают теорему о циркуляции вектора Н: циркуляция вектора напряжённости магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром.

В вакууме J = 0, поэтому Н превращается в В/μ₀ и формулы (3.8) и (3.10) переходят в формулы (2.26) и (2.24).

В соответствии с (2.23) напряжённость поля прямого тока в вакууме определяется выражением

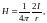(3.11)

из которого следует, что напряжённость магнитного поля имеет размерность, равную размерности силы тока, делённой на размерность длины. В связи с этим единица напряжённости магнитного поля в СИ носит название ампер на метр (А/м).

Намагниченность J принято связывать не с магнитной индукцией В, а с напряжённостью поля Н. Полагают, что в каждой точке магнетика

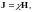(3.12)

где χ ― характерная для данного магнетика величина, называемая магнитной восприимчивостью. Опыт показывает, что для слабомагнитных (неферромагнитных) веществ, при не слишком сильных полях χ не зависит от Н. Согласно (3.7) размерность Н совпадает с размерностью J. Следовательно, χ ― безразмерная величина.

Подставив в формулу (3.7) выражение (3.12), получим

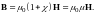(3.13)

Безразмерная величина μ = 1 + χ называется магнитной проницаемостью вещества.

В отличие от диэлектрической восприимчивости κ, которая может иметь лишь положительные значения (поляризованность Р в изотропном диэлектрике всегда направлена по полю Е (Р = κε₀Е)), магнитная восприимчивость χ бывает как положительной, так и отрицательной величиной. Поэтому магнитная проницаемость μ может быть как больше, так и меньше единицы.

Формуле (3.13) можно придать вид

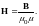(3.14)

Таким образом, напряжённость магнитного поля Н есть вектор, имеющий то же направление, что и вектор В, но в μ₀μ раз меньший по модулю (в анизотропных средах векторы Н и В, вообще говоря, не совпадают по направлению).

Граничные условия для векторов В и Н

Из соотношени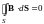й и 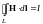легко получить условия, которым должны удовлетворять векторы В и Н на границе раздела двух магнетиков. Будем рассматривать стационарные, т. е. не изменяющиеся со временем поля.

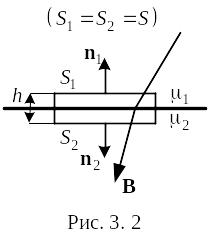Возьмём на границе двух магнетиков с проницаемостями μ₁ и μ₂ воображаемую цилиндрическую поверхность высоты h c основаниями S₁ и S₂, расположенными по разные стороны поверхности раздела (рис. 3. 2). Поток вектора В через эту поверхность равен

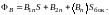(3.15)

Поток вектора В через любую замкнутую поверхность равен нулю. Приравняв нулю выражение (3.15) и сделав переход h → 0, придём к соотношению В_1n = – В_2n. Если проектировать В₁ и В₂ на одну и ту же нормаль получится условие

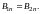(3.16)

Заменив согласно (3.14) составляющие В соответствующими составляющими вектора Н, умноженными на μ₀μ, получим соотношение

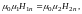
из которого следует, что

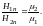
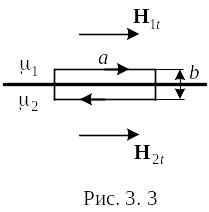(3.17)

Теперь возьмём на границе магнетиков прямоугольный контур (рис. 3. 3) и вычислим для него циркуляцию Н. При малых размерах контура циркуляцию можно представить в виде

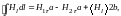(3.18)

где 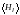― среднее значение Н_l на перпендикулярных к границе участках контура. Если по границе раздела не текут макроскопические токи, 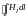в пределах контура будет равен нулю. Положив выражение (3.18) равным нулю и осуществив предельный переход b → 0, придём к соотношению

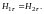(3.19)

Заменив составляющие Н, соответствующими составляющими вектора В, делёнными на μ₀μ, получим соотношение

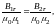
из которого следует, что

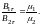(3.20)

Резюмируя, можно сказать, что при переходе через границу раздела двух магнетиков нормальная составляющая вектора В и тангенциальная составляющая вектора Н изменяются непрерывно. Тангенциальная же составляющая вектора В и нормальная составляющая вектора Н при переходе через границу раздела претерпевают разрыв. Таким образом, при переходе через границу раздела двух сред вектор В ведёт себя аналогично вектору D, а вектор Н ― аналогично вектору Е.

На рис. 3. 4 показано поведение линий В при пересечении границы раздела двух магнетиков. Обозначим углы между линиями В и нормалью к поверхности раздела соответственно α₁ и α₂. Отношение тангенсов этих углов равно

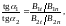
Откуда с учётом (3.16) и (3.20) получается закон преломления линий магнитной индукции

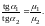(3.21)

При переходе в магнетик с большей μ линии магнитной индукции отклоняются от нормали к поверхности. Это приводит к сгущению линий. Сгущение линий В в веществе с большой магнитной проницаемостью даёт возможность формировать магнитные пучки, т. е. придавать им необходимую форму и направление. В частности, для того, чтобы осуществить магнитную защиту некоторого объёма, его окружают железным экраном.

Магнитомеханические явления.

Гиромагнитное отношение

По современным представлениям магнетизм вещества обусловлен тремя причинами: 1) орбитальным движением электронов вокруг атомных ядер, 2) собственным вращением или спином электронов, 3) собственным вращением или спином атомных ядер.

Воспользуемся простейшей боровской моделью, согласно которой электроны в атомах движутся по стационарным круговым (или эллиптическим) орбитам. Такие электроны представляют собой замкнутые электрические токи, поэтому естественно предположить, что именно они являются молекулярными токами, ответственными за намагничение вещества.

Пусть электрон движется со скоростью v по круговой орбите радиуса r. Через площадку, расположенную в любом месте на пути электрона, переносится за время t = T, равное периоду обращения электрона, заряд e. Следовательно, движущийся по орбите электрон образует круговой ток силы I = e/T. Поскольку заряд электрона отрицателен, направление движения электрона и направление тока противоположны. Магнитный момент p_me создаваемого электроном тока равен

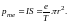
Скорость электрона 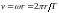, поэтому можно написать, что

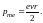
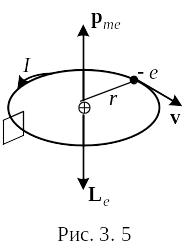
Момент p_me обусловлен движением электрона по орбите, вследствие чего называется орбитальным магнитным моментом электрона. Направление вектора p_me образует с направлением тока правовинтовую систему, а с направлением движения электрона ― левовинтовую систему (см. рис. 3. 5).

Движущийся по орбите электрон обладает моментом импульса

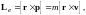
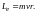
Вектор L_e называется орбитальным механическим моментом электрона. Он образует с направлением движения правовинтовую систему. Следовательно, вектор L_e противоположен по направлению вектору p_me.

Отношение магнитного момента элементарной частицы к её механическому моменту называется гиромагнитным (или магнитомеханическим) отношением. Для электрона оно равно

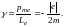(3.22)

Знак минус указывает на то, что направления моментов p_me и L_e противоположны. Связь p_me с L_e можно записать в векторной форме:

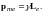(3.23)

Вследствие вращения вокруг ядра электрон оказывается подобным волчку. Это обстоятельство лежит в основе так называемых магнитомеханических явлений, заключающихся в том, что намагничение магнетика приводит к его вращению и, наоборот, вращение магнетика вызывает его намагничение. Существование первого явления было доказано экспериментально Эйнштейном и де Хаасом, второго ― Барнеттом. Описание этих опытов можно найти в учебнике И.В.Савельева т. 2, § 56. Из данных этих экспериментов было вычислено магнитомеханическое отношение, которое оказалось равным –(e/m). Таким образом, знак заряда носителей, создающих молекулярные токи, совпал со знаком заряда электрона. Однако полученный результат превысил ожидаемое значение магнитомеханического отношения (3.22) в два раза.

В дальнейшем выяснилось, что, кроме орбитальных моментов электрон обладает собственными механическим L_s и магнитным p_ms моментами, для которых магнитомеханическое отношение равно

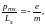(3.24)

т. е. совпадает со значением, полученным в опытах Эйнштейна и де Хааса и Барнетта. Отсюда следует, что магнитные свойства железа обусловлены не орбитальным, а собственным магнитным моментом электронов.

Диамагнетизм

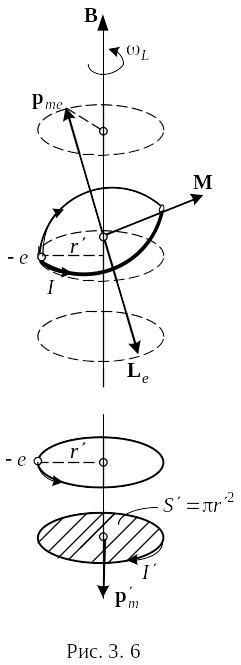
Электрон, движущийся по орбите, подобен волчку. Поэтому ему должны быть свойственны все особенности поведения гироскопов под действием внешних сил, в частности, при соответствующих условиях должна возникать прецессия электронной орбиты. Условия, необходимые для прецессии, осуществляются, если атом находится во внешнем магнитном поле В (рис. 3. 6). В этом случае на орбиту действует вращательный момент

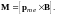
Из (3.23) видно, что вращательный момент можно выразить в форме:

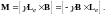
Из закона изменения момента импульса следует, что

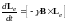и, соответственно, (3.25)

Вектор 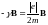совпадает по направлению с вектором В.

В курсе механики было показано, что скорость произвольной точки тела, вращающегося вокруг неподвижной точки О, может быть найдена по формуле

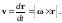
Из сопоставления этого выражения с (3.25) видно, что под влиянием внешнего магнитного поля векторы L_e и p_me орбитальных моментов электрона в атоме вращаются с угловой скоростью

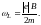(3.26)

При этом векторы L_e и p_me описывают соосные круговые конические поверхности с общей вершиной в центре орбиты и осью, параллельной В. Частоту (3.26) называют частотой ларморовой прецессии или просто ларморовой частотой.

Такое движение векторов L_e и p_me и соответствующей им орбиты электрона в атоме называется прецессией Лармора. Из формулы (3.26) видно, что угловая скорость прецессии Лармора зависит только от магнитной индукции поля и совпадает с ней по направлению.

Таким образом, доказана теорема Лармора: единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и вектора p_me с угловой скоростью ɷ_L вокруг оси, проходящей через ядро атома и параллельной вектору В индукции магнитного поля.

Прецессия орбиты обуславливает дополнительное движение электрона вокруг направления поля. Если бы расстояние r´ электрона от параллельной В оси, проходящей через центр орбиты, не изменялось, дополнительное движение происходило бы по окружности радиуса r´ (см. незаштрихованную окружность в нижней части рис. 3. 6). Ему соответствовал бы круговой ток (см. заштрихованную окружность) 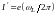, магнитный момент которого

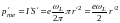(3.27)

направлен в сторону, противоположную В (см. рисунок). Этот момент называется индуцированным (наведённым) магнитным моментом.

В действительности, вследствие движения электрона по орбите, расстояние r´ всё время меняется. Поэтому в формуле (3.27) нужно брать вместо r´² его среднее во времени значение 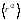. Можно показать, что

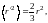(3.28)

где r ― радиус круговой орбиты электрона в атоме.

Подставив в (3.27) значение (3.26) для ɷ_L и (3.28) для , получим для среднего значения индуцированного магнитного момента одного электрона следующее выражение:

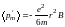(3.29)

(знак минус отражает то обстоятельство, что векторы 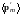и В направлены в противоположные стороны.

Просуммировав выражение (3.29) по всем электронам, найдём индуцированный магнитный момент атома

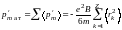(3.30)

(Z ― атомный номер химического элемента; число электронов в атоме Z).

Итак, под действием внешнего магнитного поля происходит прецессия электронных орбит с одинаковой для всех электронов угловой скоростью (3.26). Обусловленное прецессией дополнительное движение электронов приводит к возникновению индуцированного магнитного момента атома (3.30), направленного против поля.

В пределах малого объёма ∆V изотропного диамагнетика векторы 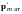всех N атомов одинаковы. Они, как видно из (3.30) пропорциональны В и противоположны ему по направлению. Поэтому намагниченность диамагнетика есть

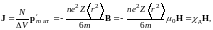
где 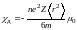― магнитная восприимчивость атомарного изотропного диамагнетика (n ― концентрация атомов, Z ― число электронов в атоме, m ― масса электрона).

Необходимо ещё выяснить, какие силы сообщают атому ларморово вращение. Это не могут сделать магнитные силы, так как они перпендикулярны скорости и работы не производят. А с ларморовым вращением связана дополнительная кинетическая энергия атома. Магнитные силы могут только поддерживать, но не создавать ларморово вращение. Последнее возникает во время включения магнитного поля. Переменное магнитное поле возбуждает вихревое электрическое поле. Оно то и сообщает атому ларморово вращение.

То есть, ларморовское вращение есть одно из проявлений электромагнитной индукции. То обстоятельство, что электромагнитная индукция должна приводить именно к диамагнетизму, а не к парамагнетизму, проще всего понять, руководствуясь правилом Ленца: магнитное поле В_инд, возбуждаемое ларморовым вращением, должно иметь такое направление, чтобы препятствовать всяким изменениям внешнего магнитного поля. Поэтому В_инд, а с ним и вектор намагничения среды J, должны иметь направление, противоположное направлению внешнего поля В. Явление электромагнитной индукции имеет место во всех средах. Поэтому обусловленный им диамагнетизм есть универсальное явление, которое должно проявляться во всех средах.

Однако в тех случаях, когда атомы сами по себе обладают магнитным моментом, магнитное поле не только индуцирует момент (3.30), но и оказывает на магнитные моменты атомов ориентирующее действие, устанавливая их по направлению поля. Возникающий при этом положительный (т. е. направленный по полю) магнитный момент бывает значительно больше, чем отрицательный индуцированный момент. Поэтому результирующий момент оказывается положительным и вещество ведёт себя как парамагнетик.

Диамагнетизм обнаруживают только те вещества, у которых атомы не обладают магнитным моментом (векторная сумма орбитальных и спиновых магнитных моментов электронов атома равна нулю).

Парамагнетизм

Если магнитный момент р_m атомов отличен от нуля, вещество оказывается парамагнитным. Магнитное поле стремится установить магнитные моменты атомов вдоль В, тепловое движение стремится разбросать их равномерно по всем направлениям. В результате устанавливается некоторая преимущественная ориентация моментов вдоль поля тем большая, чем больше В, и тем меньшая, чем выше температура.

Кюри экспериментально установил закон, согласно которому восприимчивость парамагнитного вещества равна

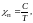(3.31)

где С ― постоянная Кюри, зависящая от рода вещества, Т ― абсолютная температура.

Классическая теория парамагнетизма была развита Ланжевеном в 1905 г. Он рассмотрел статистическую задачу о поведении молекулярных токов и соответствующих им магнитных моментов р_m в однородном магнитном поле с индукцией В. Оказалось, что намагниченность парамагнетика J в поле зависит от параметра

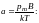
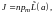
где n ― концентрация атомов (молекул) парамагнетика, функция 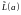называется классической функцией Ланжевена и имеет вид

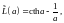
где

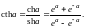
При a >>1 ≡ 1, J ≡ n р_m. Магнитные моменты всех атомов выстроены по полю и намагниченность парамагнетика практически не увеличивается при дальнейшем росте В.

Это состояние называется состоянием насыщения парамагнетика. Оно может осуществляться при очень сильных полях и очень низких температурах. В обычных условиях при не слишком сильных полях и не очень низких температурах a << 1. В этом случае 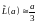и

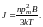
Разделив J на Н и положив В/Н = μ₀ (для парамагнетика μ практически равна единице), найдём восприимчивость:

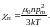(3.32)

Мы пришли к закону Кюри. Сопоставление формул (3.31) и (3.32) даёт для постоянной Кюри следующее выражение:

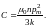
Квантовая теория парамагнетизма учитывает тот факт, что возможны лишь дискретные ориентации магнитного момента атома относительно поля. Она приводит к выражению для χ_п, аналогичному (3.32).

Ферромагнетизм

По своим магнитным свойствам все вещества можно разделить на слабомагнитные и сильномагнитные. К слабомагнитным веществам относятся парамагнетики и диамагнетики. К сильномагнитным ― ферромагнетики, антиферромагнетики и ферримагнетики. Сильный магнетизм наблюдается только у веществ в твёрдом состоянии, и притом далеко не у всех.