
физика лаб / экз / мой билет и ост / Магнетизм_1
.docxМАГНИТНОЕ ПОЛЕ
Магнитное поле в вакууме
Силы, действующие в магнитном поле на движущиеся заряды и токи.
Закон Ампера
Опыт показывает, что электрические токи взаимодействуют между собой. Механические силы взаимодействия зависят от силы этих токов и расположения проводников.
Рассмотрение сил взаимодействия электрических зарядов чрезвычайно упрощается введением понятия электрического поля этих зарядов. Взаимодействие токов существенно сложнее взаимодействия покоящихся зарядов и, соответственно этому, введение в рассмотрение понятия поля токов в ещё большей мере облегчает стоящую перед нами задачу. Поэтому мы с самого начала воспользуемся понятием поля токов, которое по исторически сложившейся терминологии называется магнитным полем, ибо постоянные магниты создают такие же поля, как и электрические токи.
Мы положим в основу изложения два экспериментальных факта, которые были установлены в ХIX веке: 1) магнитное поле действует на движущиеся заряды; 2) движущиеся заряды создают магнитное поле. Начнём с изучения магнитного поля в вакууме, а затем перейдём к изучению магнитного поля в веществе.
Закон, определяющий силу FM, действующую на движущийся точечный заряд q в магнитном поле получен обобщением опытных фактов и выражается формулой
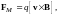 (1)
(1)
где
вектор В
не
зависит от величины заряда и его движения.
Он характеризует только магнитное поле,
в котором движется заряд q.
Вектор В
называется индукцией
магнитного поля. Сила
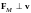 и
и
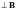 и её величина
и её величина
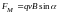 пропорциональна синусу угла между
векторами v
и В.
Когда векторы v
и В
коллинеарны,
сила FM
обращается в нуль. Формула (1) справедлива
не только для постоянных, но и для
переменных магнитных полей, и притом
при любых
значениях скорости v.
пропорциональна синусу угла между
векторами v
и В.
Когда векторы v
и В
коллинеарны,
сила FM
обращается в нуль. Формула (1) справедлива
не только для постоянных, но и для
переменных магнитных полей, и притом
при любых
значениях скорости v.
Поскольку магнитная сила FM всегда перпендикулярна скорости v, она работу над частицей не совершает. Следовательно, действуя на заряженную частицу постоянным магнитным полем, изменить её энергию нельзя.
В системе СИ единица магнитной индукции ― тесла (Тл) ― определяется так, чтобы коэффициент пропорциональности в формуле (1) был равен единице.
Существенное отличие магнитного поля от поля электрического состоит в том, что на покоящийся заряд магнитное поле не действует. Индикатором электрического поля служит покоящийся заряд, индикатором магнитного поля ― движущийся заряд.
Формула
(1) указывает принципиальный способ
измерения магнитного поля В
по силе, действующей на движущийся
заряд. Для этого с помощью неподвижного
заряда надо сначала убедиться, что
электрического поля нет. Затем надо
найти такое направление скорости v,
при
котором
FM
обращается в нуль. Тем самым с точностью
до знака определяется направление
магнитного поля В.
Наконец, надо измерить силу FM,
когда заряд движется перпендикулярно
к В
с
какой-то скоростью
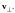 Очевидно,
Очевидно,
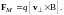
Умножая
это соотношение векторно на
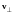 и принимая во внимание, что
и принимая во внимание, что
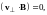 получим
получим
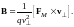 (2)
(2)
Этой формулой вектор В определяется однозначно и по величине и по направлению.
В электрическом поле Е на заряд q действует сила FЭ = qЕ. Если электрическое и магнитное поля действуют независимо, а такое предположение согласуется с опытными фактами, то при совместном действии электрического и магнитного полей возникает сила F = FЭ + FM, т. е.
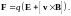 (3)
(3)
Она называется силой Лоренца.
В нерелятивистском приближении сила F, как и всякая другая сила, не зависит от выбора инерциальной системы отсчёта. Между тем второе слагаемое в формуле (3) меняется при переходе от одной системы отсчёта к другой. Поэтому должно меняться и первое слагаемое qЕ. Таким образом, разделение полной силы на электрическую и магнитную зависит от выбора системы отсчёта. Без указания системы отсчёта такое разделение теряет смысл.
Логично было бы по аналогии с напряжённостью электрического поля Е назвать В напряжённостью магнитного поля. Однако по историческим причинам основную характеристику магнитного поля назвали магнитной индукцией. Название же напряжённости магнитного поля оказалось присвоенным вспомогательной величине Н, аналогичной вспомогательной характеристике D электрического поля.
Опыты
по действию магнитного поля на движущиеся
заряды проще проводить не с отдельными
зарядами, а с электрическими токами,
когда в движение вовлекается сразу
очень много заряженных частиц. Допустим,
что ток создаётся движением одинаковых
частиц с зарядом e
и концентрацией n,
тогда плотность тока j
= env.
Число
частиц в объёме dV
будет
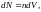 а сила, действующая в магнитном поле
на элемент объёма тела dV,
а сила, действующая в магнитном поле
на элемент объёма тела dV,
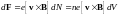
или
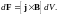 (4)
(4)
Конечно, это выражение справедливо и в более общем случае, когда носителями тока являются разные заряды.
Рассмотрим частный случай, когда ток I течёт вдоль тонкого цилиндрического провода с площадью поперечного сечения S. Возьмём бесконечно короткий участок провода длины dl и вычислим действующую на него силу dF. Если dV=Sdl объём этого участка, то
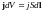 или
или
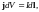 (5)
(5)
причём направление вектора dl совпадает с направлением тока. Вектор jdV называется объёмным, а Idl ― линейным элементом тока. Из (4) и (5) получаем:

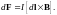 (6)
(6)
Формула (6), определяющая силу, действующую в магнитном поле на линейный элемент тока, была установлена Ампером и носит название закона Ампера. Сила, действующая на провод конечной длины, найдётся из (6) интегрированием по всей длине провода:
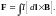 (7)
(7)
Силы, действующие на токи в магнитном поле, называются амперовыми силами.
Магнитное поле равномерно движущегося заряда.
Закон Био и Савара.
Сформулируем закон, определяющий магнитное поле движущегося точечного заряда, ограничиваясь при этом равномерным движением с малыми скоростями (v << c). Такой закон был получен обобщением опытных данных и выражается формулой:

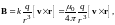 (8)
(8)
где r ― радиус-вектор, проведённый от заряда в точку наблюдения (рис. 1), а k ― коэффициент пропорциональности, зависящий от выбора системы единиц. В системе СИ k полагают равным μ0/4π, где μ0 ― магнитная постоянная, равная
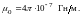 (9)
(9)
Используем
приведённые формулы для вычисления сил
взаимодействия двух движущихся точечных
зарядов q1
и q2.
Это взаимодействие складывается из
электрического (по закону Кулона) и
магнитного. Ниже речь идёт только о
магнитном взаимодействии. Пусть v1
и v2
означают скорости движущихся зарядов
(рис.2). Индукция магнитного поля,
создаваемого зарядом q1
в точке нахождения заряда q2,
будет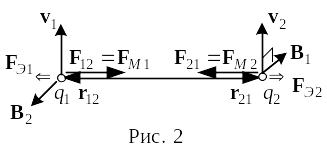
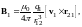
где r21 ― радиус-вектор, проведённый от первого заряда ко второму. На заряд q2 это поле действует с силой
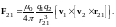 (10)
(10)
Аналогично, заряд q2 действует на заряд q1 с силой
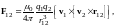 (11)
(11)
где r12 ― радиус-вектор, проведённый от заряда q2 к заряду q1.
Рассмотрим два одноимённых точечных заряда q1 и q2, движущихся вдоль параллельных прямых с одинаковой скоростью v, много меньшей скорости света с. При малых скоростях электрическое поле практически не отличается от поля неподвижных зарядов. Поэтому величину электрической силы FЭ, действующей на заряды, можно считать равной
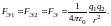 (12)
(12)
Согласно формулам (10) и (11) для магнитной силы FМ, действующей на заряды, получается выражение
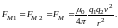 (13)
(13)
Найдём отношение магнитной силы к электрической. Из (12) и (13) следует, что
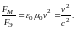 (14)
(14)
Мы получили соотношение (14) в предположении, что v << c. Однако это соотношение оказывается справедливым при любых v.
Направления сил FЭ и FМ противоположны. Рисунок выполнен для одноимённых и притом положительных зарядов. Для одноимённых отрицательных зарядов направления сил останутся теми же, а направления векторов В1 и В2 изменятся на противоположные. Для разноимённых зарядов направления электрических и магнитных сил будут противоположны показанным на рисунке.
Из (14) следует, что магнитная сила слабее кулоновской на множитель, равный квадрату отношения скорости заряда к скорости света. Это объясняется тем, что магнитное взаимодействие между движущимися зарядами является релятивистским эффектом. Магнетизм исчез бы, если бы скорость света оказалась бесконечно большой.
Формула
(14) показывает, что отношение силы
магнитного взаимодействия движущихся
зарядов к силе их кулоновского
взаимодействия пропорциональна
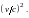 Скорость упорядоченного движения
электронов в металлах порядка нескольких
см/с, а в электролитах и того меньше.
Таким образом
Скорость упорядоченного движения
электронов в металлах порядка нескольких
см/с, а в электролитах и того меньше.
Таким образом
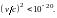 Почему же электродвигатели приводят в
движение именно амперовы силы, по
сравнению с которыми силы электростатического
взаимодействия не играют никакой роли?
Всё дело в том, что в переносе тока
участвует громадное число частиц, и это
обстоятельство компенсирует малость
множителя
При
этом существенно, что действие магнитного
поля на движущийся заряд q
определяется не q
и v
в
отдельности, а произведением этих
величин: qv.
Когда течёт ток, то заряды противоположных
знаков движутся в противоположных
направлениях, так что произведение qv
имеет
для них один и тот же знак. Точно так же
магнитные поля, возбуждаемые движущимися
зарядами, зависят от произведения qv,
а потому поля противоположных по знаку
зарядов, как и силы, действующие на
частицы противоположных знаков в
магнитном поле, арифметически складываются.
Совсем иначе ведут себя электрические
заряды по отношению к электрическим
полям. Силы, действующие на положительные
и отрицательные заряды, направлены
противоположно, а потому арифметически
вычитаются. С другой стороны, даже в
электрически заряженном теле заряды
определённого знака в значительной
степени скомпенсированы зарядами
противоположного знака. Как бы ни был
велик электрический заряд тела, всё же
он ничтожно мал по сравнению с суммарным
зарядом входящих в него частиц одного
знака. Вот почему магнитные силы намного
превосходят электрические силы,
действующие на нескомпенсированные
заряды тел.
Почему же электродвигатели приводят в
движение именно амперовы силы, по
сравнению с которыми силы электростатического
взаимодействия не играют никакой роли?
Всё дело в том, что в переносе тока
участвует громадное число частиц, и это
обстоятельство компенсирует малость
множителя
При
этом существенно, что действие магнитного
поля на движущийся заряд q
определяется не q
и v
в
отдельности, а произведением этих
величин: qv.
Когда течёт ток, то заряды противоположных
знаков движутся в противоположных
направлениях, так что произведение qv
имеет
для них один и тот же знак. Точно так же
магнитные поля, возбуждаемые движущимися
зарядами, зависят от произведения qv,
а потому поля противоположных по знаку
зарядов, как и силы, действующие на
частицы противоположных знаков в
магнитном поле, арифметически складываются.
Совсем иначе ведут себя электрические
заряды по отношению к электрическим
полям. Силы, действующие на положительные
и отрицательные заряды, направлены
противоположно, а потому арифметически
вычитаются. С другой стороны, даже в
электрически заряженном теле заряды
определённого знака в значительной
степени скомпенсированы зарядами
противоположного знака. Как бы ни был
велик электрический заряд тела, всё же
он ничтожно мал по сравнению с суммарным
зарядом входящих в него частиц одного
знака. Вот почему магнитные силы намного
превосходят электрические силы,
действующие на нескомпенсированные
заряды тел.
Получим теперь закон, определяющий магнитное поле отдельного элемента тока. Исходим из принципа суперпозиции, согласно которому магнитные поля отдельных движущихся зарядов векторно складываются, причём каждый заряд возбуждает поле, совершенно не зависящее от наличия других зарядов. С использованием формулы (8) принцип суперпозиции приводит к следующему выражению для магнитного поля объёмного элемента тока:
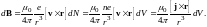 (15)
(15)
Аналогично, для линейного элемента тока получаем:
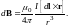 (16)
(16)
Эти формулы выражают так называемый закон Био и Савара. Полное поле найдётся интегрированием выражений (15) и (16) по всем токам, то есть
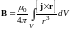 (17)
(17)
или
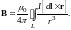 (18)
(18)
Оба этих выражения применимы лишь для постоянных токов.
Расчёт магнитных полей с помощью закона Био и Савара.
Взаимодействие параллельных токов. Единица силы тока
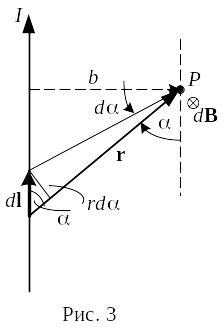 Применим
формулу (16) для вычисления поля прямого
тока, т. е. поля, создаваемого током,
текущим по тонкому прямому проводу
бесконечной длины (рис. 3). Все векторы
dB
в данной точке P
имеют одинаковое направление (в нашем
случае за чертёж). Поэтому сложение
векторов dB
можно
заменить сложением их модулей. Точка
Р,
для которой мы вычисляем магнитную
индукцию, находится на расстоянии b
от
провода. Модуль dB
определяется
выражением
Применим
формулу (16) для вычисления поля прямого
тока, т. е. поля, создаваемого током,
текущим по тонкому прямому проводу
бесконечной длины (рис. 3). Все векторы
dB
в данной точке P
имеют одинаковое направление (в нашем
случае за чертёж). Поэтому сложение
векторов dB
можно
заменить сложением их модулей. Точка
Р,
для которой мы вычисляем магнитную
индукцию, находится на расстоянии b
от
провода. Модуль dB
определяется
выражением
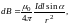 (19)
(19)
где α ― угол между векторами dl и r.
Из рис. 3 видно, что
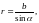
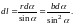
Подставим эти значения в формулу (19):
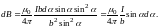
Угол α для всех элементов бесконечного прямого тока изменяется в пределах от 0 до π. Следовательно,
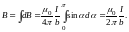
Таким образом, магнитная индукция поля прямого тока определяется формулой
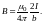
 (20)
(20)
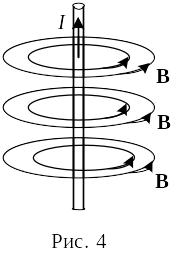
Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей (рис. 4).
 Теперь
рассчитаем силу взаимодействия двух
находящихся в вакууме параллельных
бесконечно длинных прямых токов. Если
расстояние между токами b
(рис. 5), то каждый элемент тока I2
будет находиться в магнитном поле,
индукция которого равна
Теперь
рассчитаем силу взаимодействия двух
находящихся в вакууме параллельных
бесконечно длинных прямых токов. Если
расстояние между токами b
(рис. 5), то каждый элемент тока I2
будет находиться в магнитном поле,
индукция которого равна
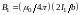 .
Угол α между элементами тока I2
и
вектором В1
прямой. Согласно (7), на элемент тока I2dl
действует сила
.
Угол α между элементами тока I2
и
вектором В1
прямой. Согласно (7), на элемент тока I2dl
действует сила
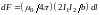 .
Следовательно, на участок второго тока
длины l
действует
сила
.
Следовательно, на участок второго тока
длины l
действует
сила
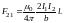 (21)
(21)
Для силы F12, действующей участок первого тока длины l, получается такое же выражение. Легко убедиться в том, что при одинаковом направлении токов они притягивают друг друга, а при различном ― отталкивают.
На основании соотношения (21) устанавливается единица силы тока в СИ. Единица силы тока в СИ ― ампер ― определяется как сила неизменяющегося тока, который , проходя по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на рсстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу, равную 2·10–7 Н на каждый метр длины.
