
физика лаб / экз / мой билет и ост / Магнетизм_2
.docxКонтур (виток) с током в магнитном поле.
Магнитный момент контура с током
Выясним, как ведёт себя контур с током в магнитном поле. Начнём со случая, когда поле однородно (В = const). На элемент контура dl действует сила
 (2.1)
(2.1)
Результирующая таких сил равна

так как I = const и В = const, то I и В можно вынести за знак интеграла:

Векторный
интеграл
 поэтому в однородном поле сила F
= 0. Это справедливо для контуров любой
формы (в том числе и не плоских) при
произвольном расположении контура
относительно направления поля. Однако
момент этой силы М,
вообще говоря, отличен от нуля. Займёмся
его вычислением.
поэтому в однородном поле сила F
= 0. Это справедливо для контуров любой
формы (в том числе и не плоских) при
произвольном расположении контура
относительно направления поля. Однако
момент этой силы М,
вообще говоря, отличен от нуля. Займёмся
его вычислением.
В дальнейшем ограничимся рассмотрением плоских контуров. Вычислим результирующий вращательный момент, создаваемый силами (2.1). Заметим, прежде всего, что поскольку в однородном поле сила, действующая на контур, равна нулю, результирующий момент относительно любой точки будет один и тот же. Действительно, результирующий момент относительно некоторой точки О определяется равенством

где
r
― радиус-вектор, проведённый из точки
О
в точку приложения силы dF.
Возьмём
точку
 ,
смещённую относительно О
на отрезок b.
Тогда
,
смещённую относительно О
на отрезок b.
Тогда
 соответственно
соответственно
 Поэтому результирующий момент относительно
точки
равен
Поэтому результирующий момент относительно
точки
равен

Рассмотрим
произвольный плоский контур с током,
находящийся в однородном магнитном
поле В.
Пусть контур с током ориентирован так,
что положительная нормаль к контуру
 (т. е. плоскость витка ̸ ̸ B)
(рис.2.1). Положительной называется
нормаль, направление которой связано
с направлением тока в контуре правилом
правого винта.
(т. е. плоскость витка ̸ ̸ B)
(рис.2.1). Положительной называется
нормаль, направление которой связано
с направлением тока в контуре правилом
правого винта.
Разобьём
площадь контура на узкие параллельные
направлению вектора В
полоски
ширины dy
(см. рис. 2.1, а; на рис. 2.1, б одна такая
полоска изображена в увеличенном виде).
На ограничивающий полоску слева элемент
контура dl1
действует сила dF1,
направленная за чертёж. Модуль этой
силы равен
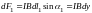 (см.
рис. 2.1, б). На ограничивающий полоску
справа элемент контура dl2
действует сила dF2,
направленная на нас. Модуль этой силы
равен
(см.
рис. 2.1, б). На ограничивающий полоску
справа элемент контура dl2
действует сила dF2,
направленная на нас. Модуль этой силы
равен

Полученный нами результат показывает, что силы, приложенные к противоположным элементам контуров dl1 и dl2, образуют пару, момент которой равен


(dS ― площадь полоски). Из рис. 2. 1 видно, что вектор dM перпендикулярен к векторам n и В и, следовательно, может быть записан в виде

Просуммировав это выражение по всем полоскам, получим вращательный момент, действующий на контур:
 (2.2)
(2.2)
(поле предполагается однородным, поэтому произведение [nхB] для всех полосок одинаково и может быть вынесено за знак интеграла. Величина S в выражении (2.2) есть площадь контура.
Выражение (2.2) можно представить в виде
 (2.3)
(2.3)
Эта
формула сходна с формулой
 определяющей
вращательный момент, действующий на
электрический диполь в электрическом
поле. Аналогом Е
служит в (2.2) вектор В,
а аналогом дипольного электрического
момента рe
― выражение ISn.
Это послужило основанием для того, чтобы
назвать величину
определяющей
вращательный момент, действующий на
электрический диполь в электрическом
поле. Аналогом Е
служит в (2.2) вектор В,
а аналогом дипольного электрического
момента рe
― выражение ISn.
Это послужило основанием для того, чтобы
назвать величину
 (2.4)
(2.4)
дипольным магнитным моментом контура с током. Направление вектора рm совпадает с направлением положительной нормали к контуру.
Формула (2.4) справедлива и для соленоида, поскольку последний можно рассматривать как систему кольцевых токов. Магнитный момент соленоида определяется формулой (2.4), если под I понимать полный ток, текущий по боковой поверхности соленоида, а под S ― площадь его поперечного сечения.
Для проволочной спирали с малым шагом, состоящей из N витков, можно написать:

Воспользовавшись обозначением (2.4), можно записать формулу (2.3) следующим образом:

 (2.5)
(2.5)
В случае, когда векторы рm и В имеют одинаковое направление, магнитные силы, действующие на отдельные участки контура, не стремятся ни повернуть контур, ни сдвинуть его с места; они лишь стремятся растянуть контур в его плоскости. Если векторы рm и В имеют противоположные направления, магнитные силы стремятся сжать контур.
В самом общем случае вращательный момент, действующий на плоский контур с током в однородном магнитном поле, определяется формулой
 (2.6)
(2.6)
Модуль вектора М равен
 (2.7)
(2.7)
Для того чтобы угол α между векторами рm и В увеличить на dα, нужно совершить против сил, действующих на контур в магнитном поле, работу
 (2.8)
(2.8)
Поворачиваясь в первоначальное положение, контур может возвратить затраченную на его поворот работу, совершив её над каким-нибудь телом. Следовательно, работа (2.8) идёт на увеличение потенциальной энергии Wp мех, которой обладает контур с током в магнитном поле,

Интегрируя, находим

Если положить const = 0, формула приобретает вид
 (2.9)
(2.9)
(ср.
с
 ).
).
Параллельная ориентация векторов рm и В отвечает минимуму энергии (2.9) и, следовательно, положению устойчивого равновесия.
Величина (2.9) представляет собой не полную потенциальную энергию контура с током, а лишь ту её часть, которая обусловлена существованием вращательного момента (2.6). Чтобы подчеркнуть это, мы снабдили символ величины (2.9) индексом «мех». Полная потенциальная энергия контура включает, кроме (2.9), ещё другие слагаемые.
Теперь рассмотрим плоский контур с током в неоднородном магнитном поле. Для простоты будем вначале считать контур круговым. Предположим, что поле быстрее всего меняется в направлении x, совпадающем с направлением В в том месте, где расположен центр контура, и что магнитный момент контура ориентирован по полю (рис. 2. 2).
 В
рассматриваемом случае В
≠
const.
и выражение
В
рассматриваемом случае В
≠
const.
и выражение
 Силы
Силы
 Составляющие
dFt
этих сил параллельны контуру и создают
усилия, растягивающие или сжимающие
контур. Составляющие же dFn,
перпендикулярные к плоскости контура,
складываясь, дадут некоторую силу F,
стремящуюся переместить
контур в магнитном поле.
Составляющие
dFt
этих сил параллельны контуру и создают
усилия, растягивающие или сжимающие
контур. Составляющие же dFn,
перпендикулярные к плоскости контура,
складываясь, дадут некоторую силу F,
стремящуюся переместить
контур в магнитном поле.
С
помощью соотношения
 найдём
выражение для силы
найдём
выражение для силы
 Если
ориентация магнитного момента по
отношению к полю остаётся неизменной
(α = const.),
то Wp
будет зависеть только от x
(через В).
Для проекции силы на ось x
получаем:
Если
ориентация магнитного момента по
отношению к полю остаётся неизменной
(α = const.),
то Wp
будет зависеть только от x
(через В).
Для проекции силы на ось x
получаем:

По предположению, в других направлениях поле изменяется слабо, поэтому проекциями силы на другие оси можно пренебречь и считать, что F = Fx. Итак,
 (2.10)
(2.10)
Согласно полученной нами формуле сила, действующая на контур с током в неоднородном магнитном поле, зависит от ориентации магнитного момента контура относительно направления поля. Если векторы рm и В совпадают по направлению (α = 0), сила положительна, т. е. направлена в сторону возрастания В (контур втягивается в область более сильного поля). Если рm и В антипараллельны (α = π), сила отрицательна, т. е. направлена в сторону убывания В (контур выталкивается из поля).
Разумеется,
что, кроме силы F,
на контур в неоднородном магнитном
поле будет действовать также вращательный
момент

Магнитное поле контура с током
 Рассмотрим
поле, создаваемое током, текущем по
тонкому проводнику, имеющего форму
окружности радиуса R
(круговой ток). Найдём индукцию магнитного
поля В
на
оси кругового тока на расстоянии x
от центра контура (рис. 2.3).
Рассмотрим
поле, создаваемое током, текущем по
тонкому проводнику, имеющего форму
окружности радиуса R
(круговой ток). Найдём индукцию магнитного
поля В
на
оси кругового тока на расстоянии x
от центра контура (рис. 2.3).
Векторы
dB
перпендикулярны
к плоскостям, проходящим через
соответствующий элемент dl
и
точку, в которой мы ищем поле. Из
соображений симметрии можно заключить,
что результирующий вектор В
направлен
вдоль оси контура. Каждый из составляющих
векторов dB
вносит
в результирующий вектор вклад dB//,
равный по модулю
 Угол
α между dl
и
r
прямой,
поэтому
Угол
α между dl
и
r
прямой,
поэтому

Проинтегриров
по всему контуру и заменив r
на
 ,
получим
,
получим
 (2.11)
(2.11)
Эта формула определяет величину магнитной индукции на оси кругового тока. Приняв во внимание, что векторы В и pm имеют одинаковое направление, можно написать формулу (2.11) в векторном виде:
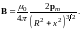 (2.12)
(2.12)
Это выражение не зависит от знака x. Следовательно, в точках оси, симметричных относительно тока, В имеет одинаковую величину и направление.
При x = 0 формула (2.12) переходит в формулу для магнитной индукции в центре кругового тока:
 (2.13)
(2.13)
На больших расстояниях от контура в знаменателе можно пренебречь R3 по сравнению с x3. Тогда формула (2.12) принимает вид
 (на
оси тока), (2.14)
(на
оси тока), (2.14)
аналогичный
выражению
 для напряжённости электрического поля
на оси диполя.
для напряжённости электрического поля
на оси диполя.
Можно показать, что любой системе токов или движущихся зарядов, локализованной в ограниченной части пространства, можно приписать магнитный момент pm (сравни с дипольным электрическим моментом системы зарядов). Магнитное поле такой системы определяется формулой
 (2.15)
(2.15)
В частности поле плоского контура любой формы на больших расстояниях имеет вид
 (2.16)
(2.16)
где r ― расстояние от контура до данной точки, θ ― угол между направлением вектора pm и напрвлением от контура в данную точку поля. При θ = 0 формула (2.16) даёт для модуля вектора В такое же значение, как и формула (2.14).
Из всего сказанного в предыдущем и в данном параграфе вытекает, что дипольный магнитный момент является весьма важной характеристикой контура с током. Этой характеристикой определяется как поле, создаваемое контуром, так и поведение контура во внешнем магнитном поле.
Работа, совершаемая при перемещении тока в магнитном поле
 Рассмотрим
контур с током, образованный неподвижными
проводами и скользящей по ним подвижной
перемычкой длины l
(рис. 2. 4). Допустим, что этот контур
находится во внешнем магнитном поле,
которое мы будем предполагать однодным
и перпендикулярным к плоскости контура.
При уазанных на рис. 2. 4 направлениях
тока и поля сила F,
действующая на перемычку, будет направлена
вправо и равна
Рассмотрим
контур с током, образованный неподвижными
проводами и скользящей по ним подвижной
перемычкой длины l
(рис. 2. 4). Допустим, что этот контур
находится во внешнем магнитном поле,
которое мы будем предполагать однодным
и перпендикулярным к плоскости контура.
При уазанных на рис. 2. 4 направлениях
тока и поля сила F,
действующая на перемычку, будет направлена
вправо и равна

При перемещении перемычки вправо на dx эта сила совершит работу

где
 ― площадь, пересечённая проводником
при движении.
― площадь, пересечённая проводником
при движении.
Если
вектор В
направлен
иначе, то его всегда можно разложить на
составляющую Вn
,
перпендикулярную к dS
,
составляющую Вt
,
параллельную dS.
Так как
 ,
то составляющая Вt
вызовет силу, перпендикулярную к dx,
и работа этой силы будет равна нулю.
Поэтому
,
то составляющая Вt
вызовет силу, перпендикулярную к dx,
и работа этой силы будет равна нулю.
Поэтому
 (2.17)
(2.17)
где
 ―
есть магнитный поток через заштрихованный
прямоугольник.
―
есть магнитный поток через заштрихованный
прямоугольник.
Рассмотрм
теперь вращательное движение проводника.
Пусть элемент длины проводника dl
,
входящий в цепь тока, поворачивается
на угол dα.
(рис.
2.5). При движении он описывает площадку
 ,
где l
―
расстояние элемента от оси вращения О.
Сила, действующая на элемент dl
в
процессе его перемещения, есть Idl·Bn
, где Вn
― составляющая индукции, перпендикулярная
к S.
Поэтому совершаемая работа равна
,
где l
―
расстояние элемента от оси вращения О.
Сила, действующая на элемент dl
в
процессе его перемещения, есть Idl·Bn
, где Вn
― составляющая индукции, перпендикулярная
к S.
Поэтому совершаемая работа равна


и выражается той же формулой (2.17), что и при поступательном движении.
Но любое движение проводника можно свести к поступательному и вращательному движениям. Это значит, что формула (2.17) определяет механическую работу для произвольного перемещения проводника.
Этот результат можно выразить ещё следующим образом. Вn равно числу линий магнитной индукции, проходящих через единицу поверхности площадки dS, а Вn dS ― числу линий магнитной индукции, пересекаемых проводников при движении. Поэтому работа, совершаемая при движении проводника с током в магнитном поле, равна произведению из силы тока на число линий магнитной индукции, пересечённых проводником.
Для полной работы получается выражение
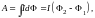 (2.18)
(2.18)
если I = const. Таким образом, работа, совершаемая магнитными силами над током равна произведению силы тока на приращение магнитного потока при перемещении проводника. Здесь Φ1 и Φ2 ― значения магнитного потока через контур в начальном и конечном положении. При перемещении проводника сила тока в нём должна оставаться постоянной.
Условимся при вычислении потока через замкнутый контур с током всегда брать в качестве n в выражении
 (2.19)
(2.19)
положительную нормаль, т. е. нормаль, образующую с направлением тока в контуре правовинтовую систему.
Если в (2.19) выражать В в тесла, а S в м2 то магнитный поток окажется также выраженным в единицах СИ ― в веберах (Вб) (Единица магнитного потока в системе СИ вводится из закона электромагнитной индукции).
Отметим, что работа (2.18) совершается не за счёт энергии внешнего магнитного поля, а за счёт источника, поддерживающем неизменным ток в контуре.
Теорема Гаусса для вектора магнитной индукции
Найдём
поток вектора В
через
произвольную замкнутую поверхность S.
Согласно правилу проведения линий В,
величина
 равна
количеству линий В,
пронизывающих площадку dS.
Следовательно, поток вектора В,
который
определяется
формулой
равна
количеству линий В,
пронизывающих площадку dS.
Следовательно, поток вектора В,
который
определяется
формулой
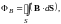 численно
равен количеству пересечений N
линий В
с
поверхностью S.
Пересечение нужно рассматривать как
алгебраическую величину. Это означает,
что пересечения, соответствующие выходу
линий из данного объёма наружу (в этом
случае угол α острый), нужно брать со
знаком плюс, а пересечения, возникающие
при входе линий внутрь объёма (в этом
случае угол α тупой), брать со знаком
минус. Таким образом, N
= Nвыход
– Nвход.
Между определённым таким способом
числом
N
и потоком ΦВ
,
имеется числовое равенство
численно
равен количеству пересечений N
линий В
с
поверхностью S.
Пересечение нужно рассматривать как
алгебраическую величину. Это означает,
что пересечения, соответствующие выходу
линий из данного объёма наружу (в этом
случае угол α острый), нужно брать со
знаком плюс, а пересечения, возникающие
при входе линий внутрь объёма (в этом
случае угол α тупой), брать со знаком
минус. Таким образом, N
= Nвыход
– Nвход.
Между определённым таким способом
числом
N
и потоком ΦВ
,
имеется числовое равенство

Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора В не имеют ни начала, ни конца. Поэтому число пересечений, возникающих при выходе линий В из объёма, ограниченного некоторой поверхностью S, всегда равно числу пересечений, возникающих при входе линий в этот объём. Следовательно, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие
 (2.20)
(2.20)
Эта формула выражает теорему Гаусса для вектора В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
Заменив
в соотвтствии с теоремой Остроградского
― Гаусса поверхностный интеграл в
объёмный
 получим,
что
получим,
что

Это равенство должно ыполняться для любого произвольно выбранного объёма V. Это возможно лишь в том случае, если подынтегральная функция в каждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что его дивергенция равна нулю:
 (2.21)
(2.21)
Силовые поля, дивергенция которых всюду обращаются в нуль, называются соленоидальными или вихревыми полями. Следовательно, магнитное поле является полем соленоидальным. Его источником являются не магнитне заряды, электрические токи.
Т)еорема о циркуляции индукции магнитного поля в вакууме
Обратимся к циркуляции вектора В. По определению циркуляция равна интегралу

П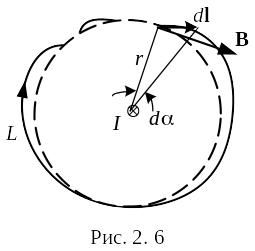 роще
всего вычислить этот интеграл в случае
поля прямого тока. Пусть замкнутый
контур лежит в плоскости, перпендикулярной
к току (рис. 2. 6; ток перпендикулярен к
плоскости чертежа и направлен за чертёж).
В каждой точке контура вектор В
направлен
по касательной к окружности, проходящей
через эту точку. Заменим в выражении
для циркуляции В·dl
через
ВdlВ
(dlВ
―
проекция элемента контура на напрвление
вектора
В).
Из рисунка видно, что
dlВ равно
rdα,
где r
―
расстояние от провода с током до dl,
dα
― угол, на котрый поворачивается
радиальная прямая при перемещении вдоль
контура на отрезок dl.
Таким образом, подставив выражение для
роще
всего вычислить этот интеграл в случае
поля прямого тока. Пусть замкнутый
контур лежит в плоскости, перпендикулярной
к току (рис. 2. 6; ток перпендикулярен к
плоскости чертежа и направлен за чертёж).
В каждой точке контура вектор В
направлен
по касательной к окружности, проходящей
через эту точку. Заменим в выражении
для циркуляции В·dl
через
ВdlВ
(dlВ
―
проекция элемента контура на напрвление
вектора
В).
Из рисунка видно, что
dlВ равно
rdα,
где r
―
расстояние от провода с током до dl,
dα
― угол, на котрый поворачивается
радиальная прямая при перемещении вдоль
контура на отрезок dl.
Таким образом, подставив выражение для
 получим
получим
 (2.22)
(2.22)
 С
учётом равенства (2.22) имеем
С
учётом равенства (2.22) имеем

При
обходе по контуру, охватывающему ток,
радиальная прямая всё время поворачивается
в одном направлении, поэтому
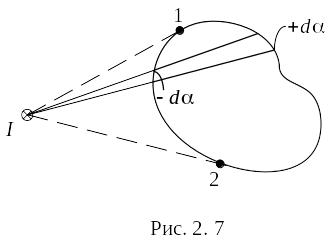
 Иначе обстоит дело, если ток не охватывается
контуром (рис. 2. 7). В этом случае при
обходе по контуру радиальная прямая
поворачивается сначала в одном направлении
(участок 1―2), а затем в противоположном
(участок 2 ― 1), вследствие чего
Иначе обстоит дело, если ток не охватывается
контуром (рис. 2. 7). В этом случае при
обходе по контуру радиальная прямая
поворачивается сначала в одном направлении
(участок 1―2), а затем в противоположном
(участок 2 ― 1), вследствие чего
 равен нулю. Учтя этот результат, можно
написать
равен нулю. Учтя этот результат, можно
написать
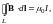 (2.23)
(2.23)
где под I следует подразумевать ток, охватываемый контуром L. Если контур тока не охватывает, циркуляция вектора В равна нулю.
Знак выражения (2.23) зависит от направления обхода по контуру (в этом же направлении отсчитывается угол α). Если направление обхода образует с направлением тока правовинтовую систему, величина (2.23) положительна, в противном случае ― отрицательна. Знак можно учесть, полагая I алгебраической величиной, причём положительным нужно считать ток, направление которого связано с направлением обхода по контуру правилом правого винта, ток противоположного направления будет отрицательным.
 С
помощью соотношения (2.23) легко восстановить
формулу для поля прямого тока. В качестве
контура интегрирования L
возьмём
окружность радиуса r
с центром на оси провода (рис. 2. 8). В
кажлой
точке контура вектор В
одинаков
по величине и направлен по касательной
к окружности. Следовательно, циркуляция
равна произведению В
на
длину окружности 2πr,
и соотношение (2.23) имеет вид
С
помощью соотношения (2.23) легко восстановить
формулу для поля прямого тока. В качестве
контура интегрирования L
возьмём
окружность радиуса r
с центром на оси провода (рис. 2. 8). В
кажлой
точке контура вектор В
одинаков
по величине и направлен по касательной
к окружности. Следовательно, циркуляция
равна произведению В
на
длину окружности 2πr,
и соотношение (2.23) имеет вид

Отсюда

Случай неплоского контура отличается от рассмотренного выше случая плоского контура лишь тем, что при перемещении вдоль контура радиальная прямая не только поворачивается вокруг провода, но и перемещается вдоль него. Все выкладки, приведшие нас к формуле (2.23), остаются справедливыми, если под dα подразумевать угол, на который поворачивается проекция радиальной прямой на перпендикулярную к току плоскость. Суммарный угол поворота этой проекции равен 2π, если контур охватывает ток, и нулю в противном случае. Следовательно, мы снова приходим к формуле (2.23).
Формула (2.23) получена для прямого тока. Можно показать, что она справедлива и для тока, текущего по проводу произвольной формы, например, для кругового тока.
Допустим, что некоторый контур охватывает несколько проводов с токами. В силу принципа суперпозиции

Каждый из интегралов в этой сумме равен μ0Ik . Следовательно,
 (2.24)
(2.24)
Итак, доказана теорема: циркуляция вектора индукции магнитного поля постоянных токов в вакууме по всякому замкнутому контуру равна сумме токов, пронизывающих контур, умноженной на μ0, причём токи Ik считаются положительными или отрицательными в зависимости от того составляют ли их направления с направлением положительного обхода контура L, право- или левовинтовую систему.
Если
плотность тока j
конечна,
то
 где
S
― любая поверхность, натянутая на контур
L,
по которому вычисляется циркуляция.
При этом формула (2.24) перейдёт в следующую:
где
S
― любая поверхность, натянутая на контур
L,
по которому вычисляется циркуляция.
При этом формула (2.24) перейдёт в следующую:
 (2.25)
(2.25)
Преобразовав
левую часть по теореме Стокса
 придём к равенству
придём к равенству

