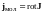25) Теорема о циркуляции вектора магнитной индукции в интегральной и дифференциальной форме.

_{Циркуляция вектора индукции магнитного поля постоянных токов в вакууме по всякому замкнутому контуру равна сумме токов, пронизывающих контур, умноженной на μ0, причём токи Ik считаются положительными или отрицательными в зависимости от того составляют ли их направления с направлением положительного обхода контура L, право- или левовинтовую систему.}

26) Поле тороида и соленоида.

_{Тороид представляет собой провод, навитый на каркас, имеющий форму тора (рис.2. 9).}

_{В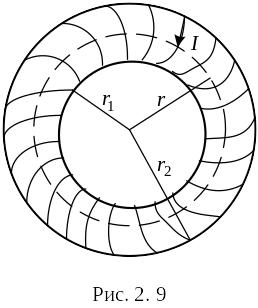 озьмём контур в виде окружности радиуса r, центр которой совпадает с центорм тороида. В силу симметрии вектор В в каждой точке должен быть направлен по касательной к контуру. Следовательно, циркуляция В равна}

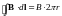
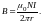
_{Поле внутри катушки не вполне однородно. Индукция наибольшая у внутренней стороны катушки 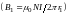и наименьшая у внешней стороны}

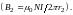
_{Любой отрезок тороида при радиусе стремящееся к бесконечности перейдет в прямую катушку или соленоид. Индукцию поля внутри соленоида можно найти из формулы}

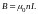
_{У конца полубесконечного соленоида на его оси магнитная индукция равна половине значения}

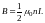
Вопрос 27: Работа при перемещении проводника с током в магнитном поле

П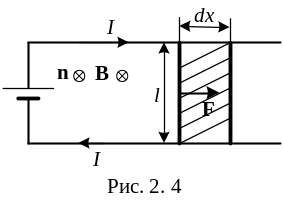 усть проводник l, входящий в цепь и находящийся в однородном, перпендикулярном l и dx, магнитном поле, перемещается поступательно на отрезок dx Со стороны магнитного поля на l будет действовать сила:

F = i*l*B

Тогда, механическая работа:

dA=F*dx=i*l*B*dx=i*B*dS

где dS = l*dx – площадь, описанная l

Если вектор B направлен по другому, то его можно разложить на составляющие, одна из которых перпендикулярна dS, а другая – параллельна dS. Параллельная составляющая вызовет силу перпендикулярную к dx, работа которой равна нулю.

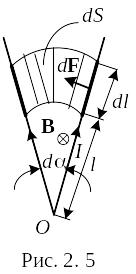
Пусть теперь dl, входящий в цепь проводника, поворачивается в магнитном поле на угол dα.Он описывает площадь: dS = l*dα*dl.

Сила, действующая на dl :

F = i*l*B_n ,

где B_n – перпендикулярная составляющая магнитной индукции, тогда работа:

dA=F*dx=i*l*B*dα*dl=i*B*dS

Так как любое движение можно свести к поступательному и вращательному, то эти формулы определяют работу для произвольного перемещения проводника.

Введя понятие магнитного потока, dФ = B_n*dS, где B_n – проекция на нормаль площадки dS, формулу для работы можно представить так:

dA = i*dФ

Если проводник совершает конечное перемещение, то:

A = i*(Ф₂ – Ф₁),

где Ф₂ и Ф₁ – поток в конечном и начальном положении.

Вопрос 28: Магнитное поле в веществе. Магнетики. Вектор намагниченности. Токи намагничивания. Плотность токов намагничивания.

Всякое вещество, под действием магнитного поля способно намагничиваться. Такие вещества называются магнетиками.

Результирующее магнитное поле в среде является суммой полей, создаваемых токами( В₀ ) и намагниченной средой (В´)

В = В₀ + В´.

Причина намагничивания заключается в том, что расположение молекулярных токов, становится частично или полностью упорядоченным. До намагничивания токи расположены беспорядочно.

Каждый молекулярный ток обладает моментом p_m = i*S*n. До намагничивания их(молекулярных токов) суммарный магнитный момент равен нулю, после – отличен от нуля. Магнитное состояние в-ва можно охарактеризовать магнитным моментом единицы объема, а именно, вектором намагниченности J:

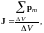
где ∆V ― физически бесконечно малый объём, взятый в окрестности рассматриваемой точки, p_m ― магнитный момент отдельной молекулы.

Молекулярные токи (токи намагничения) ― мельчайшие замкнутые электрические токи. Из-за неполной компенсации этих токов могут возникнуть поверхностные токи.

Плотность токов намагничения j_мол может быть выражена через намагниченность магнетика J: