23. Контур с током в магнитном поле. Магнитный момент контура с током. Потенциальная энергия контура с током в магнитном поле.

1)Поле однородно (В = const). На элемент контура dl действует сила

(2.1)

Результирующая таких сил равна

так как I = const и В = const, то I и В можно вынести за знак интеграла:

Векторный интеграл поэтому в однородном поле сила F = 0.

Результирующий момент относительно некоторой точки О определяется равенством

r ― радиус-вектор, проведённый из точки О в точку приложения силы dF. Возьмём точку , смещённую относительно О на отрезок b. Тогда соответственно Поэтому результирующий момент относительно точки равен

Разобьём площадь контура на узкие параллельные направлению вектора В полоски ширины dy . На ограничивающий полоску слева элемент контура dl₁ действует сила dF₁, направленная за чертёж. Модуль этой силы равен (см. рис. 2.1, б). На ограничивающий полоску справа элемент контура dl₂ действует сила dF₂, направленная на нас. Модуль этой силы равен

Полученный нами результат показывает, что силы, приложенные к противоположным элементам контуров dl₁ и dl₂, образуют пару, момент которой равен

(dS ― площадь полоски). Вектор dM перпендикулярен к векторам n и В и,

Просуммировав это выражение по всем полоскам, получим вращательный момент, действующий на контур:

Выражение (2.2) можно представить в виде

(2.3)

Эта формула сходна с формулой определяющей вращательный момент, действующий на электрический диполь в электрическом поле.

Дипольным магнитным моментом

(2.4)

дипольным магнитным моментом контура с током. Направление вектора р_m совпадает с направлением положительной нормали к контуру.

Модуль вектора М равен

(2.8)

Поворачиваясь в первоначальное положение, контур может возвратить затраченную на его поворот работу, совершив её над каким-нибудь телом. Работа (2.8) идёт на увеличение потенциальной энергии W_{p мех}, которой обладает контур с током в магнитном поле,

Если положить const = 0, формула приобретает вид

(2.9)

(ср. с ).

2)В ≠ const. Силы Составляющие dF_t этих сил параллельны контуру и создают усилия, растягивающие или сжимающие контур. Составляющие же dF_n, перпендикулярные к плоскости контура, складываясь, дадут некоторую силу F, стремящуюся переместить контур в магнитном поле.

С помощью соотношения найдём выражение для силы Если ориентация магнитного момента по отношению к полю остаётся неизменной (α = const.), то W_p будет зависеть только от x (через В). Для проекции силы на ось x получаем:

По предположению, в других направлениях поле изменяется слабо, поэтому проекциями силы на другие оси можно пренебречь и считать, что F = F_x. Итак,

(2.10)

На контур в неоднородном магнитном поле будет действовать также вращательный момент

24) Поток магнитной индукции. Теорема Гаусса для вектора магнитной индукции в интегральной и дифференциальной форме.

_{Поток вектора В, который определяется формулой численно равен количеству пересечений N линий В с поверхностью S.}

_{Для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие (диф форма)}

_{Эта формула выражает теорему Гаусса для вектора В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.}

_{Заменив в соотвтствии с теоремой Остроградского ― Гаусса поверхностный интеграл в объёмный 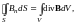получим, что (интегральная форма, но хз)}