22. Магнитное поле равномерно движущегося заряда. Закон Био и Савара. Принцип суперпозиции магнитных полей. Поле прямого тока. Поле кругового контура с током.

Магнитное поле равномерно движущегося заряда.

Сформулируем закон, определяющий магнитное поле движущегося точечного заряда, ограничиваясь при этом равномерным движением с малыми скоростями (v << c).

(8)

r ― радиус-вектор, проведённый от заряда в точку наблюдения, k ― коэффициент пропорциональности, зависящий от выбора системы единиц. В СИ k = μ₀/4π, где μ₀ ― магнитная постоянная.

(9)

Вычисление сил взаимодействия двух движущихся точечных зарядов q₁ и q₂. Пусть v₁ и v₂ скорости движущихся зарядов (рис.2). Индукция магнитного поля, создаваемого зарядом q₁ в точке нахождения заряда q₂, будет

r₂₁ ― радиус-вектор, проведённый от первого заряда ко второму. Для q₂ : (10)

q₂ действует на q₁ с силой:

(11)

где r₁₂ ― радиус-вектор, проведённый от q₂ к q₁.

Рассмотрим два одноимённых точечных заряда q₁ и q₂, движущихся вдоль параллельных прямых с одинаковой скоростью v, много меньшей скорости света с. При малых скоростях электрическое поле практически не отличается от поля неподвижных зарядов. Электрическая сила F_Э, действующей на заряды:

(12)

Согласно формулам (10) и (11) для магнитной силы F_М, действующей на заряды:

(13)

Найдём отношение магнитной силы к электрической. Из (12) и (13) следует, что

(14)

При v << c ,но оно справедливо при любых v.

Направления сил F_Э и F_М противоположны. Для одноимённых отрицательных зарядов направления сил останутся теми же, а направления векторов В₁ и В₂ изменятся на противоположные. Для разноимённых зарядов направления электрических и магнитных сил будут противоположны показанным на рисунке.

Из (14) следует, что магнитная сила слабее кулоновской на множитель, равный квадрату отношения скорости заряда к скорости света. Это объясняется тем, что магнитное взаимодействие между движущимися зарядами является релятивистским эффектом. Магнетизм исчез бы, если бы скорость света оказалась бесконечно большой.

Принцип суперпозиции магнитных полей. Закон Био и Савара.

Закон, определяющий магнитное поле отдельного элемента тока. Исходим из принципа суперпозиции, согласно которому магнитные поля отдельных движущихся зарядов векторно складываются, причём каждый заряд возбуждает поле, совершенно не зависящее от наличия других зарядов. С использованием формулы (8) принцип суперпозиции приводит к следующему выражению для магнитного поля объёмного элемента тока:

(15)

Для линейного элемента тока:

(16)

Эти формулы выражают закон Био и Савара. Полное поле найдётся интегрированием выражений (15) и (16) по всем токам

(17)

или

(18)

Оба этих выражения применимы для постоянных токов.

Поле прямого тока.

Применим формулу (16) для вычисления поля прямого тока, т. е. поля, создаваемого током, текущим по тонкому прямому проводу бесконечной длины (рис. 3). Все векторы dB в данной точке P имеют одинаковое направление (у нас за чертёж). Поэтому сложение векторов dB можно заменить сложением их модулей. Точка Р, для которой мы вычисляем магнитную индукцию, находится на расстоянии b от провода. Модуль dB определяется выражением

(19)

α ― угол между векторами dl и r.

Из рис. 3 видно, что

Подставим их в формулу (19):

Угол α для всех элементов бесконечного прямого тока изменяется в пределах от 0 до π. Следовательно,

Магнитная индукция поля прямого тока:

(20)

Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей (рис. 4).

Силу взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов. Если расстояние между токами b (рис. 5), то каждый элемент тока I₂ будет находиться в магнитном поле, индукция которого равна . Угол α между элементами тока I₂ и вектором В₁ прямой. Согласно (7), на элемент тока I₂dl действует сила . Следовательно, на участок второго тока длины l действует сила

(21)

Для силы F_12, действующей участок первого тока длины l, получается такое же выражение. Легко убедиться в том, что при одинаковом направлении токов они притягивают друг друга, а при различном ― отталкивают.

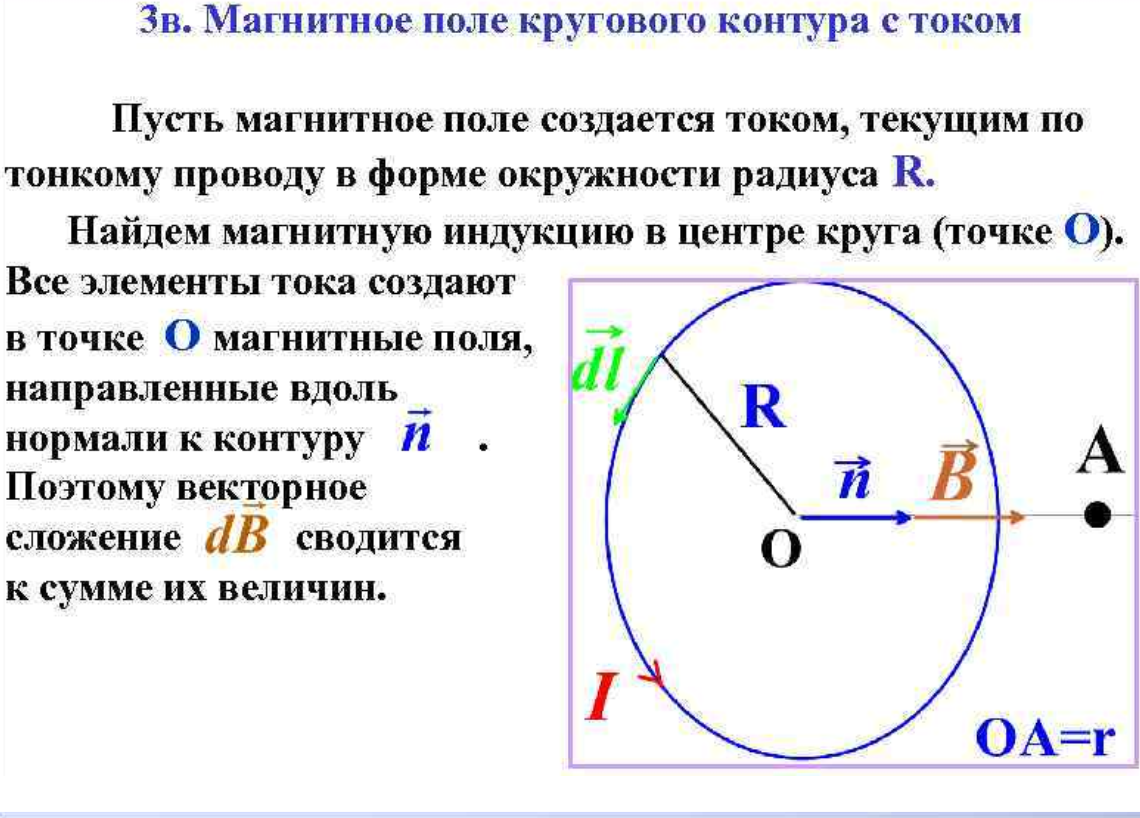
Поле кругового контура с током.