9. Электроемкость уединённого проводника. Электроёмкость уединённого шара.

Емкостью уединенного проводника, т.е. проводника, бесконечно удаленного от всех остальных проводников, называется величина заряда, потребного для сообщения этому проводнику потенциала, равного единице. При этом полагается, что аддитивная постоянная в выражении потенциала выбрана так, чтобы в бесконечности потенциал равнялся нулю.

Емкость уединенного шара численно равна его радиусу. Внешний потенциал поля радиуса а и заряда е равен  = е/R. На поверхности шара R = a и  = е/а. таково же значение потенциала и внутри всего шара. Потенциал шара будет равняться единице при е = ф, а это и значит, что емкость С шара равна а: С = а.

10. Конденсаторы. Емкость конденсатора. Соединения конденсатора. Емкость плоского, цилиндрического и сферического конденсаторов.

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника (q) к разности потенциалов между этими двумя проводниками.

Для измерения электрической емкости применяется единица, называемая фарад.

Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (смешанно).

Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (смешанно).

Последовательное соединение конденсаторов

При таком соединении конденсаторы соединены последовательно друг за другом, то есть конец одного конденсатора соединяется с началом другого. Все конденсаторы принадлежат одному проводу, на котором нет разветвлений.

Смешанное соединение

Представляет с собой различные сочетания параллельного и последовательного соединений. Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности.

Величина емкости конденсаторов определяется геометрией конденсатора (формой и размерами обкладок и величиной зазора между ними), а также диэлектрическими свойствами среды, заполняющей пространство между обкладками. Найдем формулу для ёмкости плоского конденсатора. Если площадь обкладки S, а заряд на ней q, то напряженность поля между обкладками равна

Разность потенциалов между обкладками равна

Отсюда для емкости плоского конденсатора получается формула

Где s – площадь обкладки, d – величина зазора между обкладками,  - диэлектрическая проницаемость вещества, заполняющего зазор.

Если пренебречь рассеянием поля вблизи краев обкладок, нетрудно получить для емкости цилиндрического конденсатора формулу

Где l – длина конденсатора, R₁ и R₂ – радиусы внутренней и внешней обкладок.

Емкость сферического конденсатора равна

Где R₁ и R₂ – радиусы внутренней и внешней обкладок.

11. Диэлектрики. Полярные и неполярные молекулы. Поляризуемость молекулы. Поляризация диэлектриков. Вектор поляризации. Диэлектрическая восприимчивость.

Диэлектриками называются вещества, не способные проводить электрический ток.

У симметричных молекул ( таких как Н₂, О₂, N₂) в отсутствие внешнего электрического поля центры тяжести положительных и отрицательных зарядов совпадают. Такие молекулы не обладают собственным дипольным моментом и называются неполярными. У несимметричных молекул ( например CO, NH, HCl и т.п.) центры тяжести зарядов разных знаков сдвинуты друг относительно друга. В этом случае молекулы обладают собственным дипольным моментом и называются полярными.

Под действием внешнего электрического поля заряды в неполярной молекуле смещаются друг относительно друга: положительные по направлению поля, отрицательные против поля. В результате молекула приобретает дипольный момент, величина которого пропорциональна напряженности поля. В рационализованной системе коэффициент пропорциональности записывают в виде ₀, где ₀ – электрическая постоянная,  - величина, называемая поляризуемостью молекулы. Учитывая, что направления р и Е совпадают, можно написать

р = ₀Е

Явление поляризации сводится к изменению положения в пространстве частиц диэлектрика, имеющих электрический заряд того или иного знака, в результате чего каждый макроскопический объем диэлектрика приобретает некоторый наведенный (индуцированный) электрический момент, которым этот объем диэлектрика до воздействия внешнего электрического поля не обладал.

Поляризация сопровождается появлением на поверхности диэлектриков связанных электрических зарядов, уменьшающих напряженность поля внутри вещества.

Степень поляризации диэлектрика характеризуется величиной, называемую

вектором поляризации (или поляризованностью). Вектор поляризации определяется

как суммарный дипольный момент единицы объема диэлектрика и равен

Где V – бесконечно малый объём диэлектрика, а – сумма дипольных моментов, заключенных в этом объёме молекул.

Единица поляризованности в СИ – Кл/м²

Вектор поляризации для любого диэлектрика зависит от свойств самого диэлектрика и от напряженности электростатического поля.

В случае изотропных диэлектриков, чьи свойства не зависят от направления, поляризованность линейно зависит от напряжённости результирующего поля:

Где  - диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика.

Диэлектрическая восприимчивость не зависит от напряженности Е и всегда >0

12

Электрическое поле в диэлектрике. Рассмотрим плоский однородный диэлектрический слой, расположенный между двумя разноименно заряженными плоскостями (рис. 2.5). Пусть напряженность электрического поля, которое создается этими плоскостями в вакууме, равна  ,

где   - поверхностная плотность зарядов на пластинах (эти заряды называют свободными). Под действием поля диэлектрик поляризуется, и на его гранях появляются поляризационные или связанные заряды. Эти заряды создают в диэлектрике электрическое поле  , которое направлено против внешнего поля  .

,

где   - поверхностная плотность связанных зарядов. Результирующее поле внутри диэлектрика

.

Поверхностная плотность связанных зарядов   меньше плотности   свободных зарядов, и не все поле E₀ компенсируется полем диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая часть обрывается на связанных зарядах (рис. 2.5). Вне диэлектрика  . Следовательно, в результате поляризации поле внутри диэлектрика оказывается слабее, чем внешнее  . Таким образом,

,

где   - диэлектрическая проницаемость среды. Из формулы видно, что диэлектрическая проницаемость показывает, во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике. Для вакуума  , для диэлектриков  .

Если положительные и отрицательные заряды, смещенные относительно друг друга, имеют одну и ту же среднюю плотность, то сам факт их смещения не приводит к появлению суммарного заряда внутри объема. С другой стороны, если бы   в одном месте был больше, а в другом меньше, то это означало бы, что в некоторые области попало больше зарядов, чем оттуда вышло; тогда мы бы могли получить объемную плотность заряда. В случае плоского конденсатора предположим, что   — величина постоянная, поэтому достаточно будет только посмотреть, что происходит на поверхностях. На одной поверхности отрицательные заряды (электроны) эффективно выдвинулись на расстояние  , а на другой поверхности они сдвинулись внутрь, оставив положительные заряды снаружи на эффективном расстоянии  . Возникает, как показано на фиг. 10.5, поверхностная плотность зарядов, которую мы будем называть поляризационным зарядом.

Этот заряд можно подсчитать следующим образом. Если площадь пластинки равна  , то число электронов, которое окажется на поверхности, есть произведение   и   (числа электронов на единицу объема), а также смещения  , которое, как мы предполагаем, направлено перпендикулярно к поверхности. Полный заряд получится умножением на заряд электрона  . Чтобы найти поверхностную плотность поляризационных зарядов, индуцируемую на поверхности, разделим на  . Величина поверхностной плотности зарядов равна

.

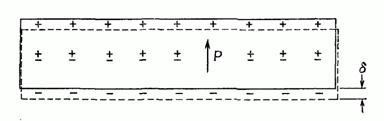
Фигура 10.5. Диэлектрик в однородном поле. Положительные заряды сместились на расстояние   относительно отрицательных.

Но она равна как раз длине   вектора поляризации   [формула (10.4)]:

.                                                                    (10.5)

Поверхностная плотность зарядов равна поляризации внутри материала. Поверхностный заряд, конечно, на одной поверхности положителен, а на другой отрицателен.

Предположим теперь, что наша пластинка служит диэлектриком в плоском конденсаторе. Пластины конденсатора также имеют поверхностный заряд (который мы обозначим  , потому что заряды в проводнике могут двигаться «свободно» куда угодно). Конечно, это тот самый заряд, который мы сообщили конденсатору при его зарядке. Следует подчеркнуть, что   существует только благодаря  . Если, разрядив конденсатор, удалить  , то   также исчезнет, но он не стечет по проволоке, которой разряжают конденсатор, а уйдет назад внутрь материала, за счет релаксации поляризации в диэлектрике.

Теперь мы можем применить теорему Гаусса к поверхности  , изображенной на фиг. 10.1. Электрическое поле   в диэлектрике равно полной поверхностной плотности зарядов, деленной на  . Очевидно, что   и   имеют разные знаки, так что

                                                         (10.6)

Заметьте, что поле   между металлической пластиной и поверхностью диэлектрика больше поля  ; оно соответствует только  . Но нас здесь интересует поле внутри диэлектрика, которое занимает почти весь объем, если диэлектрик заполняет почти весь промежуток между пластинами. Используя формулу (10.5), можно написать

.                                     (10.7)

Из этого уравнения мы не можем определить электрическое поле, пока не узнаем, чему равно  . Здесь мы, однако, предполагаем, что   зависит от   и, более того, пропорционально  . Эта пропорциональность обычно записывается в виде

.                                                                   (10.8)

Постоянная   (греческое «хи») называется диэлектрической восприимчивостью диэлектрика.

Тогда выражение (10.7) приобретает вид

,

откуда мы получаем множитель  , показывающий, во сколько раз уменьшилось поле.

Фигура 10.6. Количество заряда, прошедшее через элемент воображаемой поверхности в диэлектрике, пропорционально компоненте  , нормальной к поверхности.

Напряжение между пластинами есть интеграл от электрического поля. Раз поле однородно, интеграл сводится просто к произведению   и расстояния между пластинами  . Мы получаем

.

Полный заряд конденсатора есть   А, так что емкость, определяемая формулой (10.2),  оказывается равной

.                                (10.10)

Мы объяснили явление, наблюдавшееся на опыте. Если заполнить плоский конденсатор диэлектриком, емкость возрастает на множитель

.                                 (10.11)

который характеризует свойства данного материала. Наше объяснение останется, конечно, неполным, пока мы не объясним (а это мы сделаем позже), как возникает атомная поляризация.

Обратимся теперь к чуть более сложному случаю — когда поляризация   не всюду одинакова. Мы уже говорили, что если поляризация непостоянна, то вообще может возникнуть объемная плотность заряда, потому что с одной стороны в маленький элемент объема может войти больше зарядов, чем выйдет с другой. Как определить, сколько зарядов теряется или приобретается  в маленьком объеме?

Подсчитаем сначала, сколько зарядов проходит через воображаемую плоскость, когда материал поляризуется. Количество заряда, проходящее через поверхность, есть просто  , умноженное на площадь поверхности, если поляризация направлена по нормали к поверхности. Разумеется, если поляризация касательно, к поверхности, то через нее не пройдет ни одного заряда.

Продолжая прежние рассуждения, легко понять, что количество заряда, прошедшее через любой элемент поверхности, пропорционально компоненте  , перпендикулярной к поверхности. Сравним фиг. 10.6 и 10.5. Мы видим, что уравнение (10.5) в общем случае должно быть записано так:

.                                                              (10.12)

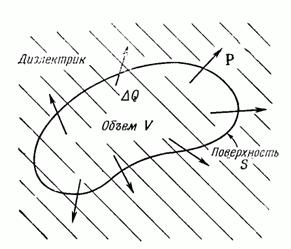
Фигура 10.7. Неоднородная поляризация  может приводить к появлению результирующего заряда внутри диэлектрика.

Если мы имеем в виду воображаемый элемент поверхности внутри диэлектрика, то формула (10.12) дает заряд, который прошел через поверхность, но не приводит к результирующему поверхностному заряду, потому что возникают равные и противоположно направленные вклады от диэлектрика по обе стороны поверхности.

Однако смещение зарядов может привести к появлению объемной плотности зарядов. Полный заряд, выдвинутый из объема   за счет поляризации, есть интеграл от внешней нормальной составляющей   по поверхности  , охватывающей объем (фиг. 10.7). Такой же излишек зарядов противоположного знака остается внутри. Обозначая суммарный заряд внутри   через  , запишем

.                             (10.13)

Мы можем отнести   за счет объемного распределения заряда с плотностью  , так что

                                                     (10.14)

Комбинируя оба уравнения, получаем

.                                              (10.15)

Мы получили разновидность теоремы Гаусса, связывающую плотность заряда поляризованного материала с вектором поляризации  . Мы видим, что она согласуется с результатом, полученным для поверхностного поляризационного заряда или же для диэлектрика в плоском конденсаторе. Уравнение (10.15) с гауссовой поверхностью  , изображенной на фиг. 10.1, дает в правой части интеграл по поверхности, равный  , а в левой части заряд внутри объема оказывается  , так что мы снова получаем  .

Точно так же, как мы делали в случае закона Гаусса для электростатики, мы можем перейти в уравнении (10.15) к дифференциальной форме, пользуясь математической теоремой Гаусса:

.

Мы получаем

.                                                           (10.16)

Если поляризация неоднородна, ее дивергенция определяет появляющуюся в материале результирующую плотность зарядов. Подчеркнем, что это совсем настоящая плотность зарядов; мы называем ее «поляризационным зарядом», только чтобы помнить, откуда она взялась.

13