1. Электри́ческий заря́д (коли́чество электри́чества) — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.

Элемента́рный электри́ческий заря́д — фундаментальная физическая постоянная, минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц. Согласно изменениям определений основных единиц СИ равен точно 1,602 176 634⋅10⁻¹⁹ Кл в Международной системе единиц (СИ).

Закон Кулона – сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.

2. Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, а также возникающее при изменении магнитного поля (например, в электромагнитных волнах).

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и равная отношению силы, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда. Напряжённость поля точечного заряда – вектор напряжённости в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд, и совпадает с силой, действующей на точечный положительный заряд, помещённый в данную точку.

Принцип суперпозиции электрических полей – если поле образовано не одним зарядом, а несколькими, то силы, действующие на пробный заряд, складываются по правилу сложения векторов. Поэтому и напряженность системы зарядов в данной точке, поля равна векторной сумме напряженностей полей от каждого заряда в отдельности.

3. Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀. где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR².

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀.

Теорема Гаусса в дифференциальной форме.

Вопрос №4 Вычисление полей с помощью теоремы Гаусса. Поле равномерно заряженной плоскости, бесконечного цилиндра, сферы. Поле шара, равномерно заряженного по объёму. (Теорему Гаусса см в вопросе №3)

Поле равномерно заряженной плоскости Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле: (dq – заряд, сосредоточенный на площади dS; dS – физически бесконечно малый участок поверхности.)

Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность   во всех точках будет иметь направление, перпендикулярное плоскости S.

В симметричных, относительно плоскости точках, напряженность   будет одинакова по величине и противоположна по направлению.

Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (см рис).

Тогда 

Применим теорему Остроградского-Гаусса.

• Поток Ф_Е через боковую часть поверхности цилиндра равен нулю, т.к.  

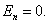
• Для основания цилиндра 

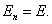
• Суммарный поток через замкнутую поверхность (цилиндр) будет равен:   

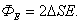
Внутри поверхности заключен заряд   . Следовательно, из теоремы Остроградского–Гаусса получим:  ; откуда следует, что

Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости 

Поле заряженного бесконечно длинного цилиндра (нити)

Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью    (dq – заряд, сосредоточенный на отрезке цилиндра).

Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.

Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси).

• Для оснований цилиндров    

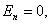
• Для боковой поверхности 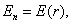  т.е. зависит от расстояния r.

• Следовательно, поток вектора    через рассматриваемую поверхность, равен 

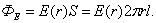
• При r>R на поверхности будет заряд 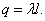 По теореме Остроградского-Гаусс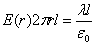а  , отсюда

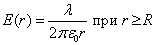
• Если r<R; E(r)=0, т.к. внутри замкнутой поверхности зарядов нет. График зависимости E(r):

Если уменьшать радиус цилиндра R (при   ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при   , получить нить.

Поле заряженной сферы

Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным,    – в любой точке проходит через центр шара.   ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r.

Если  то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда

 ,

• поле вне сферы:

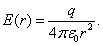
• Внутри сферы, при r<R поле будет равно нулю, т.к. там нет зарядов: E(R)=0

Как видно, вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.

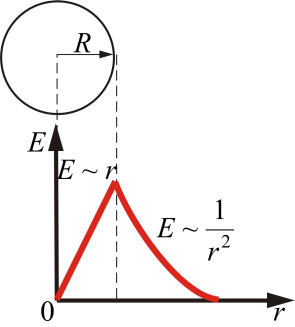Поле объемного заряженного шара

• Для поля вне шара радиусом R получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула:  .

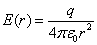• Но внутри шара при 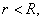  сферическая поверхность будет содержать в себе заряд, равный 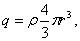(ρ – объемная плотность заряда, равная: 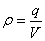  ; 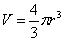    – объем шара).

Тогда по теореме Остроградского-Гаусса запишем:

, т.е. внутри шара

 

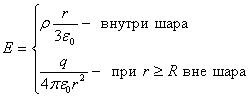
Вопрос №5 Потенциальность электростатического поля. Потенциал электростатического поля. Потенциал поля точечного заряда, равномерно заряженной металлической сферы.

Потенциальность электростатического поля

Пусть точечный заряд q перемещается по произвольной траектории в электростатическом поле из точки 1 в точку 2 под действием нескольких сил. Нас интересует сила Fэ, действующая на заряд со стороны электростатического поля. При заданном перемещении заряда она совершает работу Aэ.

Э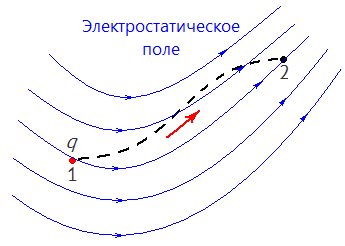 та работа не зависит от траектории, по которой перемещается заряд в электростатическом поле, а определяется только его начальным и конечным положениями (расположением точек 1 и 2). Это свойство называется потенциальностью (консервативностью). Следует понимать, что именно электростатическое поле является потенциальным, произвольное электрическое − нет.

Потенциал электростатического поля

Потенциалом φ электростатического поля называется скалярная (числовая) функция φ=φ(x,y,z) координат пространства такая, что работа сил Aэ электростатического поля при перемещении произвольного точечного заряда q по произвольной траектории из точки 1 в точку 2 равна разности значений этой функции в этих точках, умноженной на q:

Aэ=q⋅(φ1−φ2),

(φ1=φ(x1,y1,z1) − потенциальная энергия в точке 1, φ2=φ(x2,y2,z2) − потенциальная энергия в точке 2).

Потенциал поля точечного заряда

Подставим в соотношение для определения потенциала выражение для напряженности электрического поля точечного заряда:

.

При интегрировании учтем, что  .

После интегрирования получаем:

.

Потенциал точечного заряда пропорционален величине заряда и убывает обратно пропорционально расстоянию, стремясь на бесконечности к нулю.

Потенциал поля равномерно заряженной металлической сферы Получим выражение потенциала поля сферы радиуса , равномерно заряженной зарядом , как функцию расстояния до ее центра. Нулевое положение выберем на бесконечности. Возможны два случая.

• Область снаружи сферы (r>R)

В силу эквивалентности полей равномерно заряженной сферы и точечного заряда, напряженность поля в любой точке внешней области не изменится, если весь заряд сферы собрать в ее центре. Стало быть, не изменится и работа поля при движении пробного заряда по любой траектории во внешней области. А, значит, и выражение потенциальной энергии заряда в поле заряда также не изменится.

Таким образом, потенциальная энергия взаимодействия пробного заряда, находящегося за пределами равномерно заряженной сферы и самой этой сферы определяется соотношением:

Тогда, по определению потенциала, для внешней области.

• Область внутри и на границе сферы (r<=R)

При движении из внутренней области на бесконечность, заряд неизбежно пересечет границу сферы. Тогда его потенциальная энергия, по определению равная работе кулоновских сил , разлагается в сумму

Но, так как внутри равномерно заряженной сферы напряженность равна нулю, то и потенциал во всей внутренние области равен:

Вопрос №6 Связь между напряжённостью электростатического поля и потенциалом. Эквипотенциальные поверхности. Уравнение Пуассона.

Связь между напряжённостью электростатического поля и потенциалом

• Изобразим перемещение заряда q по произвольному пути l в электростатическом поле  .

Работу, совершенную силами электростатического поля на бесконечно малом отрезке dl, можно найти так:

(E_l – проекция  на  ; dl– произвольное направление перемещения заряда).

• С другой стороны, эта работа, если она совершена электростатическим полем, равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl: 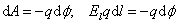, отсюда

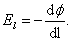
Для ориентации dl (направление перемещения) в пространстве, надо знать проекции  на оси координат:

По определению градиента сумма первых производных от какой-либо функции по координатам есть градиент этой функции, то есть

       – вектор, показывающий направление наибыстрейшего увеличения функции.

      Тогда коротко связь между   и φ записывается так: или , где  (набла) означает символический вектор, называемый оператором Гамильтона.

Знак минус говорит о том, что вектор   направлен в сторону уменьшения потенциала электрического поля.

Эквипотенциальные поверхности Совокупность точек, имеющих равный потенциал, образуют так называемые эквипотенциальное поверхности, или поверхности равного потенциала.

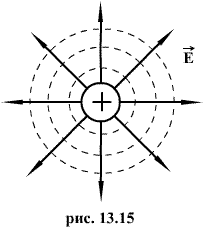С их помощью также можно графически изобразить электростатическое поле. Направление нормали к эквипотенциальной линии будет совпадать с направлением вектора   в той же точке. Эквипотенциальные поверхности можно провести через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество. Однако, проводят поверхности таким образом, чтобы разность потенциалов для двух соседних поверхностей была всюду одна и та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности. Чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности.

Уравнение Пуассона

Произвольное векторное поле E→(r→) характеризуется тремя скалярными функциями Ej(r→), где j пробегает значения x, y, z (если говорить о декартовой системе координат). Поэтому одного уравнения недостаточно, чтобы найти электрическое поле. Однако электростатическое поле потенциально. Это накладывает столь сильное ограничение, что все три компоненты E→ можно выразить через одну скалярную функцию — электрические потенциал ϕ. Подставляя E→ = −gradϕ. в уравнение divE→ = 4πρ, получаем уравнение Пуассона Δϕ = −4πρ.

где дифференциальный оператор Δ = divgrad называется оператором Лапласа, или лапласианом. В декартовой системе координат уравнение записывается следующим образом: ∂2ϕ ∂x2 + ∂2ϕ ∂y2 + ∂2ϕ ∂z2 = −4πρ.

В произвольной криволинейной системе координат для вычисления оператора Δ необходимо исходить из инвариантных определений дивергенции и градиента.

Уравнение Пуассона относится к классу дифференциальных уравнений в частных производных. Иногда специальным выбором системы координат его удается свести к обыкновенному дифференциальному уравнению. Это случается, если в такой специальной системе координат плотность заряда и потенциал зависят от одной координаты. Один пример такого рода рассмотрен далее в качестве задачи.