7. Энергия взаимодействия системы точечных зарядов (из учебника)

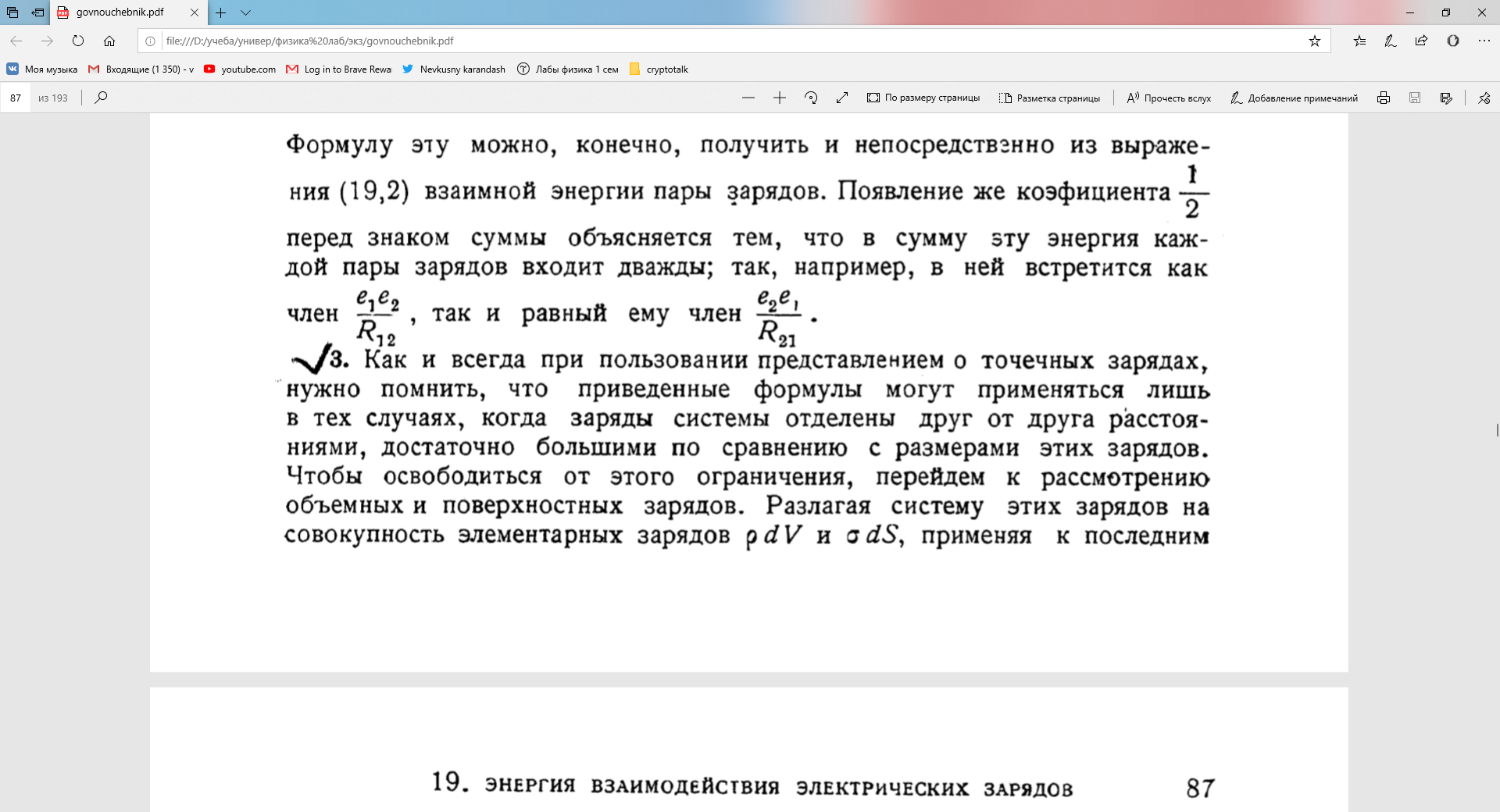
8, Электрический диполь. Момент диполя. Поле диполя. Диполь во внешнем электрическом поле.

Совокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии   друг от друга, малом по сравнению с расстоянием до рассматриваемой точки поля называется электрическим диполем.(рис.13.1)

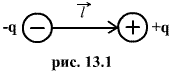
Произведение  называется моментом диполя. Прямая линия, соединяющая заряды называется осью диполя. Обычно момент диполя считается направленным по оси диполя в сторону положительного заряда. Следует отметить, что дипольный момент не зависит от положения диполя в пространстве, так как вектор    остается неизменным при любом выборе тела отсчета.

Поле диполя в дальней зоне https://tsput.ru/res/fizika/1/ELECTROSTATIKA/lection_08.html

Рассчитаем электрическое поле электрического диполя с использованием принципа суперпозиции. Особенно результат интересен на расстояниях, значительно превышающих размер диполя. Предположим, что необходимо вычислить напряженность электрического поля в точке М 

О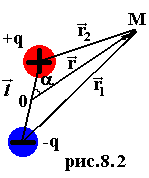 чевидно, что напряженность в произвольной точке пространства М (см. рис.8.2) по принципу суперпозиции равна

   (8.2)

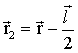где  , а  .

После подстановки имеем

   (8.3)

Подробнее рассмотрим знаменатели, считая что l>>r и a - угол между   и  . При разложении в ряд пренебрегаем последним членом.

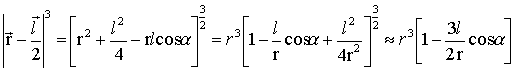
Аналогично поступаем со вторым знаменателем. При приведении к общему знаменателю в (8.3) ряд слагаемых в числителе взаимно уничтожаются, а в знаменателе пренебрегаем квадратичным членом. В итоге получаем

   (8.5)

Окончательно, учитывая, что  , имеем

    (8.6)

Это напряженность электрического поля диполя в дальней зоне, т.е. в точках пространства, где r>>l.

2.2. Электрический диполь во внешнем электрическом поле http://phys.bspu.by/static/lib/phys/bmstu/tom3/ch2/texthtml/ch2_2.htm

      Рассмотрим, каким воздействиям подвергается электрический диполь с электрическим моментом   во внешнем электростатическом поле  . В этих условиях он испытывает действие силы

     

,

(2.8)

     момента

     

(2.9)

     и приобретает потенциальную энергию

     

.

(2.10)

Для скалярной функции одного переменного справедливо приближенное выражение

     

.

(2.11)

     Это соотношение обобщается для случая скалярной функции нескольких пространственных переменных:

     

(2.12)

     Если  -радиус-вектор произвольной точки пространства,   - малый произвольный вектор с компонентами  , то выше приведенное выражение можно записать в форме:

      ,

(2.13)

     формально

     

,

(2.14)

     причем соотношение (2.14) справедливо в декартовой системе координат.

      Для векторной величины   соотношение (2.13) можно записать для каждой компоненты отдельно, а в компактной форме записи получить:

     

Зависимости (2.13) и (2.15) являются обобщением отрезка ряда Тейлора для скалярной функции одного переменного (2.11) на многомерный случай скалярного и векторного полей.
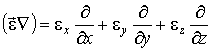