24. Зависимость теплового эффекта химической реакции от температуры (закон Кирхгоффа). Теплоемкость.

Теплоемкость

Теплоемкость С – количество теплоты, которое нужно передать, чтобы нагреть 1 градус Цельсия. Дж/К

1. Дж/(К*моль)

2. , где

3. 

Закон Кирхгоффа

Пересчитывать тепловые эффекты с одной температуры на другую

1. 1з.к.г.

2. 2з.к.г.

Температурный коэффициент теплового эффекта процесса равен изменению теплоемкости системы, происходящему в результате процесса

Проинтегрировав вышеприведенные диф. уравнения получим:

Для того, чтобы подсчитать тепловой эффект процесса при некоторой температуре , нужно знать тепловой эффект этого процесса при , а также характер изменения теплоемкости системы в интервале температур .

В небольшом температурном интервале можно в степенных рядах для теплоемкостей ограничиться только первым членом

и тогда будет величиной постоянной:

.

Обычно в роли выступает стандартная температура 298К( 25 градусов Цельсия):

.

В некоторых случаях данные по теплоемкости участников процесса отсутствуют, и тогда приходится идти на очень грубое приближение:

.

25. Второе начало термодинамики. Понятие об энтропии. Расчет энтропии. Изменение энтропии при химических процессах и фазовых переходах.

Второе начало термодинамики

Рассмотрим несколько формулировок второго закона термодинамики:

- Невозможен самопроизвольный переход тепла от тела менее нагретого к более нагретому.

- Невозможно создание вечного двигателя II рода, т.е. машины, которая периодически превращает тепло среды при постоянной температуре в работу.

- Невозможен процесс, единственным результатом которого было бы превращение теплоты в работу.

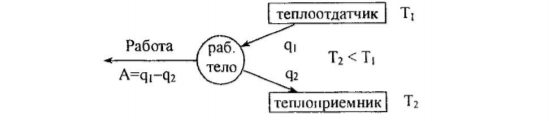
Для работы тепловой машины необходимы два тепловых резервуара с температурами T1 и T2. Рабочее тело получает некоторое количество теплоты q1 от теплоотдатчика и отдает q2 теплоприемнику. Работа равна разности q1-q2.

Термодинамический к.п.д.

- Наибольший к.п.д. тепловой машины не зависит от природы вида тел и веществ, участвующих в работе машины, а определяется только температурами теплоотдатчика и теплоприемника:

Понятие энтропии

Для изолированных систем критерием, позволяющим судить о направлении самопроизвольно протекающих процессов и об условиях равновесия, является некоторая функция состояния S-энтропия.

В изолированных системах самопроизвольно идущие процессы протекают в направлении увеличения энтропии, В момент достижения равновесия энтропия системы достигает максимума. Обратное протекание процессов не может быть самопроизвольным, для их проведения требуется затрата работы извне.

2-ое начало термодинамики, указывающее на односторонний характер протекания процессов, есть следствие молекулярной природы вещества.

Каждое состояние системы может быть охарактеризовано определенной вероятностью, при этом равновесию отвечает небольшая вероятность, следовательно, вероятность данного состояния является тем критерием, который определяет направление процесса и позволяет найти равновесие.

Функция W – термодинамическая вероятность: это число способов, которым может быть реализовано данное состояние. W – функция состояния и максимальна при равновесии.

Две системы с W1 и W2 образуют сложную систему с .

В отличие от функций H и U функция W неаддитивна. Кроме того, W связана с механическими характеристиками системы, а не с термическими.

Все вышесказанное потребовало новую вероятность функции, к которой были предъявлены два требования: наличие свойства аддитивности и экстремальные значения при равновесии. Кроме того, эта функция должна быть связана с тепловыми характеристиками системы. Этой функцией является энтропия S:

Энтропия сложного события:

.

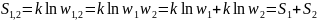При возрастании W увеличивается и S, значение которой при равновесии должно быть максимальным, как и значение W.

Связь между теплотой процесса и изменения энтропии: .

А в дифференциальном виде: .

Первый закон термодинамики: δq=T*dS, в результате чего получаем:

dU=T*dS-δA – аналитическое выражение первого и второго начал термодинамики для обратимого процесса.

Можно показать, что для необратимого расширения идеального газа будут справедливы уравнения: , .

- неравенство (>) и тождество (=) Клаузиса.

Частные производные (из тождества):

; откуда .

Подставим в частную производную вместо :

, откуда .

Аналогично можно получить уравнение и для : .

Если система изолирована, то, очевидно, δq=0, следовательно, .

Любой необратимый процесс является односторонним и самопроизвольным. Таким образом, если в изолированной системе возможен самопроизвольный процесс, то при его протекании энтропия S возрастает.

Все вышеизложенное позволяет сформулировать 2-ой закон термодинамики в следующем виде: существует функция состояния – энтропия, приращение которой при обратимых процессах равно приведенному теплу; энтропия изолированной системы стремится к максимуму.