Действия над матрицами
Произведением прямоугольной (m n)-матрицы А на число называют матрицу, элементы которой получены умножением элементов на число :
.
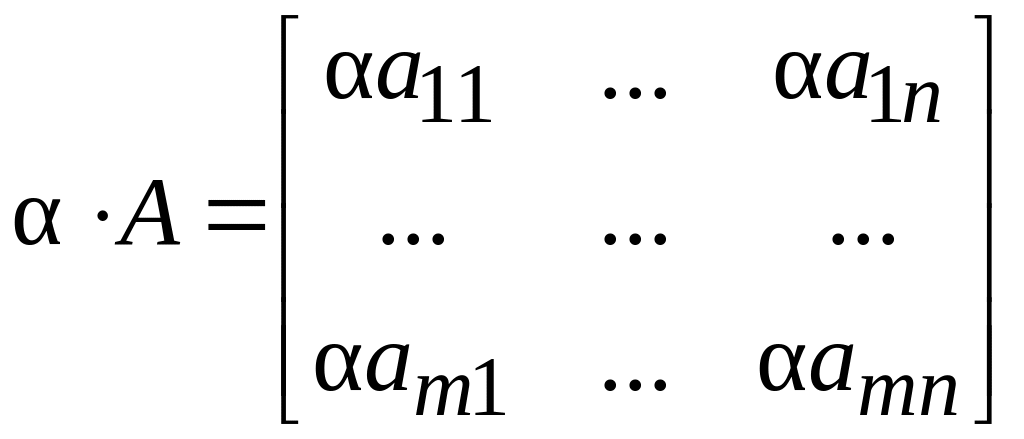Сумма определяется для прямоугольных матриц одинакового строения, и элементы суммы равны суммам соответствующих слагаемых, т. е.
Умножение
определяется только для таких прямоугольных
матриц, у которых число столбцов первого
множителя равно числу строк второго.
Произведением
(m р)-матрицы
А
на (р n)-матрицу
В
будет (m n)-матрица
С
с элементами:
.
Матрицы А и В называются перестановочными, если AB = BA. Определитель произведения двух квадратных матриц равен произведению определителей перемножаемых матриц.
Для различения операций (табл. 2.12) над матрицами по правилам линейной алгебры и поэлементных операций с массивами перед знаком операции ставят точку. Примеры использования операций с возможными особенностями их выполнения представлены в табл. 2.13.
Таблица 2.12
Операции с матрицами |
Операции с элементами матриц |
+ сложение |
+ сложение |
– вычитание |
– вычитание |
* умножение |
.* умножение |
^ возведение в степень |
.^ возведение в степень |
/ правое деление |
./ правое деление |
\ левое деление |
.\ левое деление |
' транспонирование |
|
kron тензорное произведение |
|
Таблица 2.13
Ввод матрицы a: |
Ввод матрицы b: |
Свойства определителя: |
|||
»a = [1 2 3;2 3 1;3 1 2] a = 1 2 3 2 3 1 3 1 2 |
»b = [4 5 6;5 6 4;6 4 3] b = 4 5 6 5 6 4 6 4 3 |
»det(a)*det(b) ans = 774 |
»det(a*b) ans = 774 |
||
Умножение на число: |
Сумма матриц: |
Произведение матриц: |
|||
»6.*a ans = 6 12 18 12 18 6 18 6 12 |
»a+b ans = 5 7 9 7 9 5 9 5 5 |
»a*b ans = 32 29 23 29 32 27 29 29 28 |
|||
Ввод матрицы c: |
Ввод матрицы d: |
Различают правое (справа налево) и левое деление: |
|||
»c = [1 1 1;2 2 2;3 3 3] c = 1 1 1 2 2 2 3 3 3 |
»d = [4 4 4;5 5 5;6 6 6] d = 4 4 4 5 5 5 6 6 6 |
»c.\d ans = 4.0000 4.0000 4.0000 2.5000 2.5000 2.5000 2.0000 2.0000 2.0000
»c./d ans = 0.2500 0.2500 0.2500 0.4000 0.4000 0.4000 0.5000 0.5000 0.5000 |
|||
Возведение в степень: |
|||||
»c.^2 % поэлементное ans = 1 1 1 4 4 4 9 9 9 |
»c^2 ans = 6 6 6 12 12 12 18 18 18 |
»c^0 ans = 1 0 0 0 1 0 0 0 1 |
|||
Система Matlab в режиме прямых вычислений над векторами и матрицами наряду с обычными арифметическими и алгебраическими действиями выполняет такие операции, как инвертирование матрицы, вычисление ее собственных значений и векторов, решение систем линейных уравнений, вывод графиков двумерных и трехмерных функций и многое другое.
Матрица
называется обратной
к квадратной матрице А,
если A
= E,
при
этом
.
Невырожденность
матрицы А
есть необходимое и достаточное условие
существования обратной матрицы, которая
при этом оказывается единственной и
перестановочной с исходной. Квадратная
матрица А = (
)
называется невырожденной,
если ее определитель не равен нулю; в
противном случае матрица называется
вырожденной
(особенной).
Таблица 2.14
Ввод матрицы |
Определитель |
Обратная матрица |
Проверка
|
»A = [4 6 7; 11 1 9; 2 2 2] A = 4 6 7 11 1 9 2 2 2 |
»det(A) ans = 52 |
»inv(A) ans = –0.3077 0.0385 0.9038 –0.0769 –0.1154 0.7885 0.3846 0.0769 –1.1923 |
»A*inv(A) ans = 1.0000 –0.0000 0 –0.0000 1.0000 0 0 –0.0000 1.0000 |
»B = [5 6 4; 7 10 5; 3 6 9] B = 5 6 4 7 10 5 3 6 9 |
»det(B) ans = 60 |
»inv(B) ans = 1.0000 –0.5000 –0.1667 –0.8000 0.5500 0.0500 0.2000 –0.2000 0.1333 |
»B*inv(B) ans = 1.0000 0.0000 –0.0000 –0.0000 1.0000 –0.0000 0 0.0000 1.0000 |
»inv(B*A) ans = –0.1577 –0.0058 0.1737 0.1731 –0.1827 0.1122 0.0846 0.0885 –0.2192 |
»inv(A)*inv(B) ans = –0.1577 –0.0058 0.1737 0.1731 –0.1827 0.1122 0.0846 0.0885 –0.2192 |
||
=E
Примеры
применения дополнительных операций
над матрицами показаны в табл. 2.14. Верна
формула
.