МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра Информатики

отчет

по лабораторной работе №5

по дисциплине «Информатика»

Тема: Решение уравнений и систем уравнений в Matlab

Студентка гр. 9491		Зубкова В.В.
Студент гр. 9491		Ярошук В.А.
Преподаватель		Гречухин М.Н.

Санкт-Петербург

2019

Содержание

Цель работы 3

Требования и рекомендации к выполнению задания 3

Основные теоритические положения 3

Решение уравнений вида 3

Решение систем линейных уравнений 3

Способ 1. Метод обратной матрицы 4

Способ 2. Метод Крамера. 4

Способ 3. Метод Гаусса. 5

Ход работы 6

Вывод 10

Цель работы

Решение уравнений и систем уравнений разными способами в системе Matlab.

Требования и рекомендации к выполнению задания

1. Решить уравнение

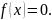
2. Решить систему уравнений, методом обратной матрицы, Крамера и Гаусса. Вывести на экран все три результата и убедиться, что они совпадают.

Основные теоритические положения

Решение уравнений вида

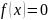
Для простоты будем рассматривать случай, когда 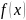- полином, т. е. имеет вид 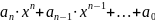. Тогда, согласно следствию из основной теоремы алгебры, уравнение имеет ровно 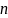в общем случае комплексных корней.

Для нахождения корней многочлена в Matlab используется функция roots. Полином задаётся в виде вектора коэффициентов при степенях , т. е. имеет вид .

Решение систем линейных уравнений

Система линейных алгебраических уравнений в самом общем случае имеет вид:

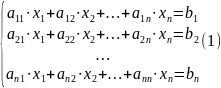
Для вычислений в Matlab удобно представлять такую систему в виде матрицы коэффициентов 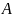и вектора свободных членов :

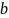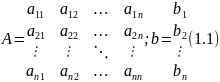
Тогда систему (1) можно записать в виде:

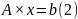
где 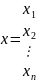– вектор-столбец неизвестных.

Способ 1. Метод обратной матрицы

Если , то тогда система (1) имеет единственное решение, которое выражается как

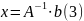
Таким образом, нам необходимо посчитать обратную матрицу для матрицы коэффициентов и перемножить её со столбцом свободных членов.

Пример 2. Решение системы методом обратной матрицы

А= [1 -2 1; 2 -5 -1; -7 0 1];

B=[2; -1; -2];

x=inv(A)*b – решение системы x=A-1b

Способ 2. Метод Крамера.

Суть метода Крамера состоит в следующем. Если для представления системы уравнений (1.1) соблюдается условие , то система имеет единственное решение следующего вида:

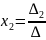
и т. д., где

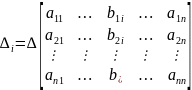
т. е. определитель матрицы А (1.1), в которой 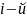столбец заменён столбцом свободных членов .

Пример 3. Решение системы методом Крамера

A=[1 2 3 4; -1 -2 -3 4; 0 1 -1 1; 1 1 1 1];

B=[30; 10; 3; 10];

% Проверим невырожденность системы

rank(A)

>> ans = 4

% По правилу Крамера по очереди заменяем столбцы исходной матрицы столбцом свободных членов. Для этого создаем 4 копии матрицы – по числу столбцов

А1 = А;

А2 = А;

А3 = А;

А4 = А;

А1(:,1) = b;

A2(:,2) = b;

A3(:,3) = b;

A4(:,4) = b;

% Вычисляем определители

x1 = det(A1) / det(A);

x2 = det(A2) / det(A);

x3 = det(A3) / det(A);

x4 = det(A4) / det(A);

x=[x1;x2;x3;x4]4

Способ 3. Метод Гаусса.

Метод Гаусса предполагает проведение преобразований с так называемой расширенной матрицей системы уравнений, т. е. с матрицей вида 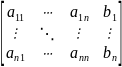с целью приведения её к виду .

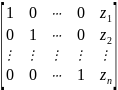Последний столбец будет содержать значения неизвестных. Система будет иметь единственное решение, когда

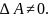
В Matlab для решения систем уравнений методом Гаусса используется встроенная функция rref.

Пример 4. Решение системы уравнений методом Гаусса

A = [1 2 3; 1 -3 2; 1 1 1];

b = [7; 5; 3];

% Формируем расширенную матрицу системы

C = [A b];

% Приведем ее к ступенчатому виду, выпонив прямой и обратный ход метода Гаусса

D = rref(C)

D =

1 0 0 1

0 1 0 0

0 0 1 2

Ход работы

Вариант 4

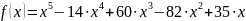
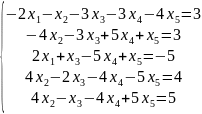
Решение уравнений вида

>> x=[1 -14 60 -82 35]

x =

1 -14 60 -82 35

>> y=roots(x)

y =

7

5

1 +1.9231e-008i

1 -1.9231e-008i

Метод обратной матрицы

>> A=[-2 -1 -3 -3 -4; 4 -4 -2 1 -4; 3 -5 0 4 2; 0 5 2 -2 -2; -4 -2 -5 -1 4]

A =

-2 -1 -3 -3 -4

4 -4 -2 1 -4

3 -5 0 4 2

0 5 2 -2 -2

-4 -2 -5 -1 4

>> b=[3; 5; 0; 2; 5]

b =

3

5

0

2

5

>> x=inv(A)*b

x =

-13.524

14.667

-14

35.286

-13.619

Метод Крамера

>> A=[-2 -1 -3 -3 -4; 4 -4 -2 1 -4; 3 -5 0 4 2; 0 5 2 -2 -2; -4 -2 -5 -1 4]

A =

-2 -1 -3 -3 -4

4 -4 -2 1 -4

3 -5 0 4 2

0 5 2 -2 -2

-4 -2 -5 -1 4

>> b=[3; 5; 0; 2; 5]

b =

3

5

0

2

5

>> rank(A)

ans =

5

>> A1 = A

A1 =

-2 -1 -3 -3 -4

4 -4 -2 1 -4

3 -5 0 4 2

0 5 2 -2 -2

-4 -2 -5 -1 4

>> A2 = A

A2 =

-2 -1 -3 -3 -4

4 -4 -2 1 -4

3 -5 0 4 2

0 5 2 -2 -2

-4 -2 -5 -1 4

>> A3 = A

A3 =

-2 -1 -3 -3 -4

4 -4 -2 1 -4

3 -5 0 4 2

0 5 2 -2 -2

-4 -2 -5 -1 4

>> A4 = A

A4 =

-2 -1 -3 -3 -4

4 -4 -2 1 -4

3 -5 0 4 2

0 5 2 -2 -2

-4 -2 -5 -1 4

>> A5=A

A5 =

-2 -1 -3 -3 -4

4 -4 -2 1 -4

3 -5 0 4 2

0 5 2 -2 -2

-4 -2 -5 -1 4

>> x= det(A1) / det(A)

x =

1

>> A1(:,1) = b

A1 =

3 -1 -3 -3 -4

5 -4 -2 1 -4

0 -5 0 4 2

2 5 2 -2 -2

5 -2 -5 -1 4

>> A2(:,2) = b

A2 =

-2 3 -3 -3 -4

4 5 -2 1 -4

3 0 0 4 2

0 2 2 -2 -2

-4 5 -5 -1 4

>> A3(:,3) = b

A3 =

-2 -1 3 -3 -4

4 -4 5 1 -4

3 -5 0 4 2

0 5 2 -2 -2

-4 -2 5 -1 4

>> A4(:,4) = b

A4 =

-2 -1 -3 3 -4

4 -4 -2 5 -4

3 -5 0 0 2

0 5 2 2 -2

-4 -2 -5 5 4

>> A5(:,5) = b

A5 =

-2 -1 -3 -3 3

4 -4 -2 1 5

3 -5 0 4 0

0 5 2 -2 2

-4 -2 -5 -1 5

>> x1= det(A1) / det(A)

x1 =

-13.524

>> x2= det(A2) / det(A)

x2 =

14.667

>> x3= det(A3) / det(A)

x3 =

-14

>> x4= det(A4) / det(A)

x4 =

35.286

>> x5= det(A5) / det(A)

x5 =

-13.619

>> x=[x1;x2;x3;x4;x5]

x =

-13.524

14.667

-14

35.286

-13.619

Метод Гаусса

>> A=[-2 -1 -3 -3 -4; 4 -4 -2 1 -4; 3 -5 0 4 2; 0 5 2 -2 -2; -4 -2 -5 -1 4]

A =

-2 -1 -3 -3 -4

4 -4 -2 1 -4

3 -5 0 4 2

0 5 2 -2 -2

-4 -2 -5 -1 4

>> b=[3; 5; 0; 2; 5]

b =

3

5

0

2

5

>> C = [A b]

C =

-2 -1 -3 -3 -4 3

4 -4 -2 1 -4 5

3 -5 0 4 2 0

0 5 2 -2 -2 2

-4 -2 -5 -1 4 5

>> D = rref(C)

D =

1 0 0 0 0 -13.524

0 1 0 0 0 14.667

0 0 1 0 0 -14

0 0 0 1 0 35.286

0 0 0 0 1 -13.619

>> x = D(:,5)

x =

0

0

0

0

1

Вывод

Научились решать уравнения вида и системы уравнений методом обратных матриц, методом Крамера и методом Гаусса.