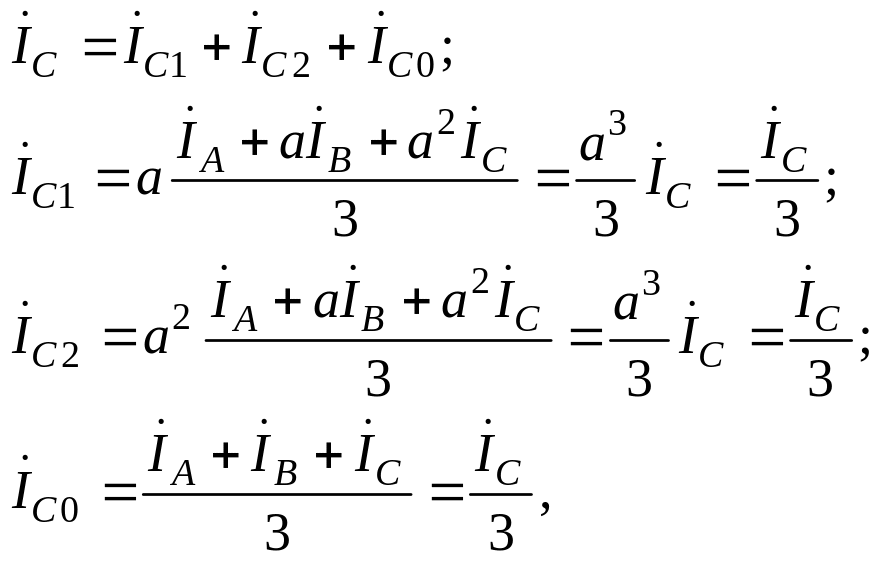новая папка / РГР 3

Методические указания к заданию № 3

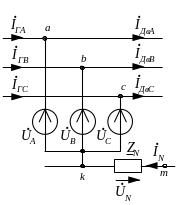
Для заданной схемы дано:

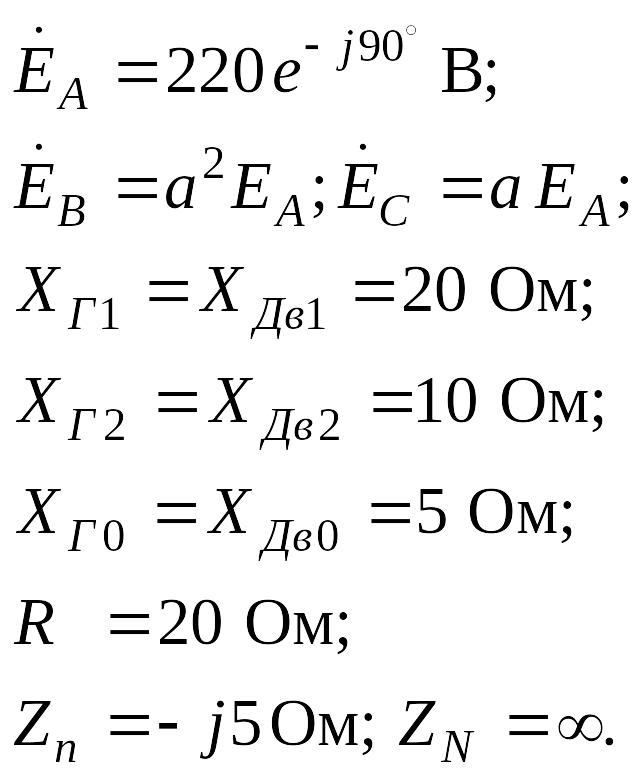
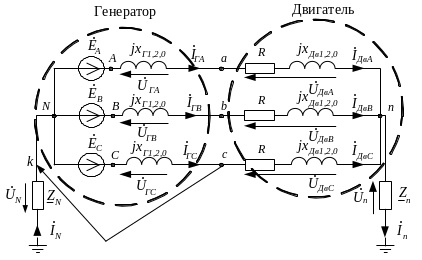
1. Короткое замыкание фазы С на нейтраль N генератора.

Для особой фазы С рассчитываем симметричные составляющие напряжений и токов.

1. В место повреждения вводим фиктивные ЭДС , , 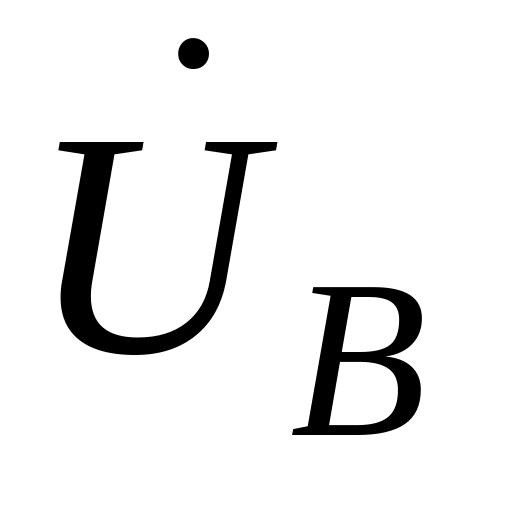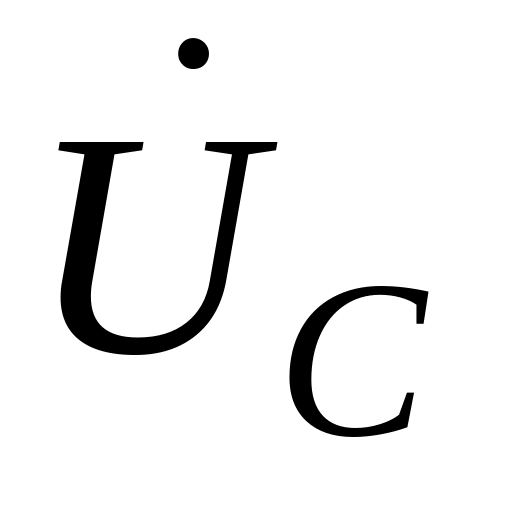и записываем условие: .

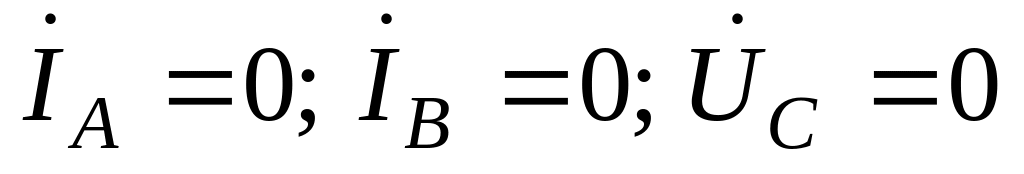В результате: где

2. Расчётная схема прямой последовательности для особой фазы С:

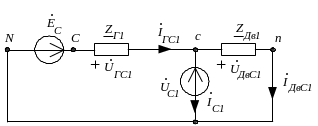
где

Складываем параллельные ветви с и , получаем эквивалентную схему:

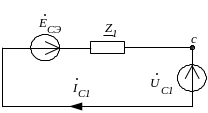
где

– эквивалентное сопротивление прямой последовательности;

В

– эквивалентная ЭДС фазы С.

В результате на основании законов Ома и Кирхгофа можно записать расчётные формулы:

Расчёт по этим формулам будет возможен после определения составляющей тока короткого замыкания прямой последовательности фазы С, т.е. .

3. Расчётная схема обратной последовательности для особой фазы С:

где

Складываем параллельные ветви с и , получаем эквивалентную схему:

;

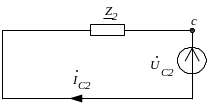
– эквивалентное сопротивление обратной последовательности.

В результате на основании законов Ома и Кирхгофа можно записать расчётные формулы:

Расчёт по этим формулам будет возможен после определения составляющей тока короткого замыкания обратной последовательности фазы С, т.е. .

4. Расчётная схема нулевой последовательности для особой фазы С:

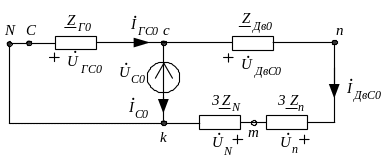
где

– эквивалентное сопротивление нулевой последовательности.

В результате на основании законов Ома и Кирхгофа можно записать расчётные формулы:

Расчёт по этим формулам будет возможен после определения составляющей тока короткого замыкания обратной последовательности фазы С, т.е. .

Рассчитываем симметричные составляющие напряжений и токов особой фазы С.

Так как

и , то

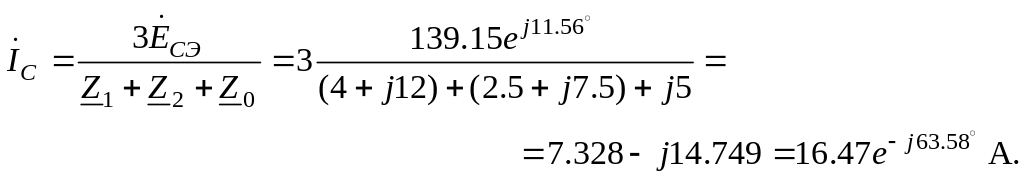
В результате по вышеприведённым формулам находим симметричные составляющие прямой последовательности напряжений и токов фазы С:

Далее находим симметричные составляющие обратной последовательности напряжений и токов фазы С:

,

причём – верно.

Затем находим симметричные составляющие нулевой последовательности напряжений и токов фазы С:

2. Определяем напряжения и токи трёхфазной цепи, используя найденные симметричные составляющие фазы С и фазовый оператор :

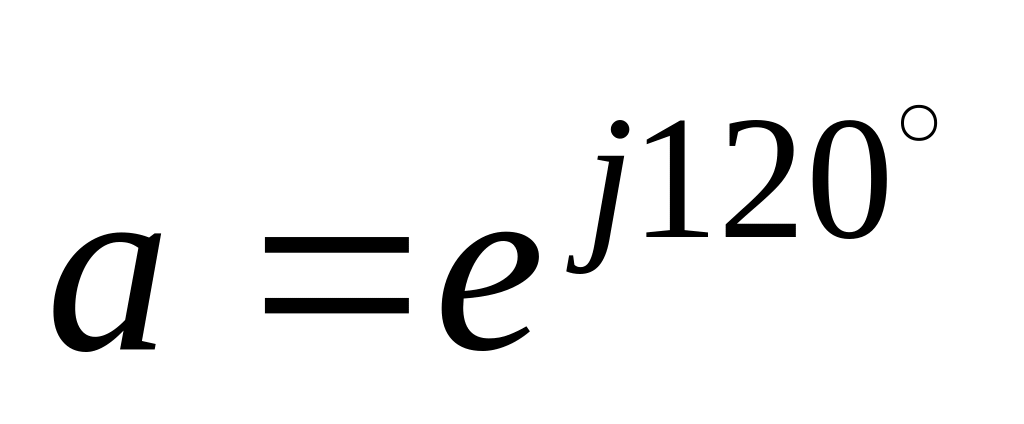– верно, т.к.

При замыкании фазы С на N и при имеем:

– верно.

3. Рассчитываем балансы активной и реактивной мощностей.

1. Комплекс полной вырабатываемой мощности:

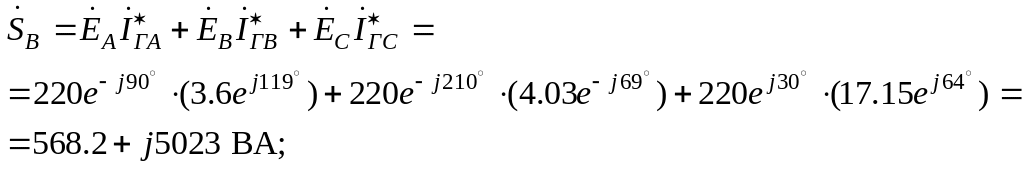
где – активная вырабатываемая мощность;

– реактивная вырабатываемая мощность.

2. Потери полной мощности в обмотках генератора:

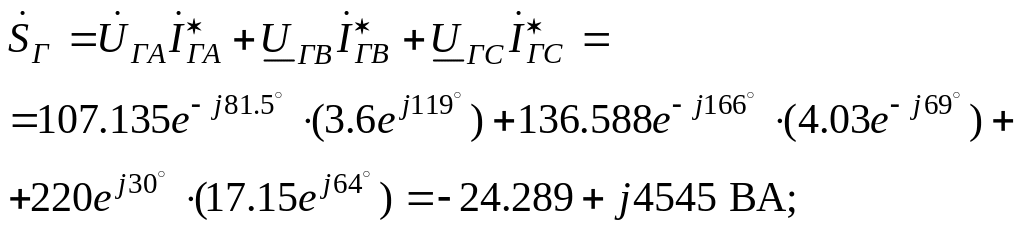
; , т.к. и .

3. Потребляемая двигателем полная мощность:

где ; .

4. Потребляемая в нулевом проводе полная мощность.

где ; .

5. Потребляемая активная 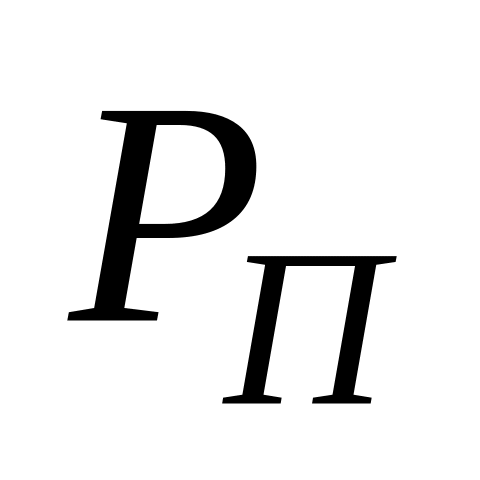и реактивная 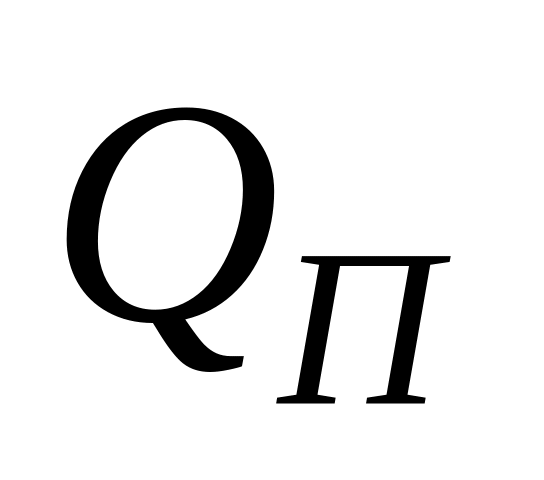мощности:

.

6. Относительные погрешности:

– верно.

4. Для построения векторной диаграммы напряжений рассчитываем комплексные потенциалы узлов схемы. Для этого примем

тогда

– верно.

Выбираем для вещественной и мнимой осей масштаб напряжений и рассчитанные потенциалы узлов с учётом этого масштаба наносим на комплексную плоскость. Направляем между полученными точками векторы ЭДС и напряжений. Выбираем масштаб тока и строим лучевую векторную диаграмму для токов генератора , , . Один из векторов токов или напряжений, например , представим в виде суммы векторов прямой, обратной и нулевой последовательностей. 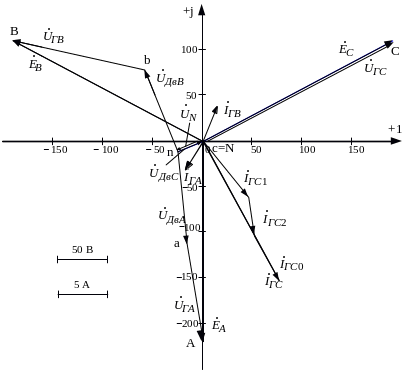Векторная диаграмма представлена на рис. 3.8.

5. Проанализировать полученные результаты и сформулировать выводы по работе, указав при этом какие составляющие токов и напряжений получились наибольшими (по модулю) и наименьшими (по модулю), какие результирующие токи и напряжения получились равными (по модулю) и почему.

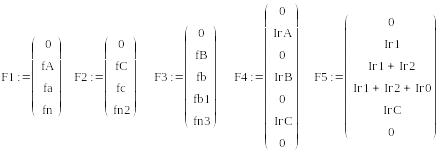
Расчет РГР №3 при помощи программы MathCad осуществляется следующим образом:

8. Векторная диаграмма напряжений и токов.

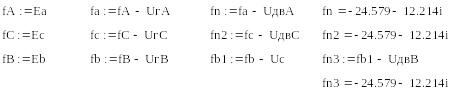
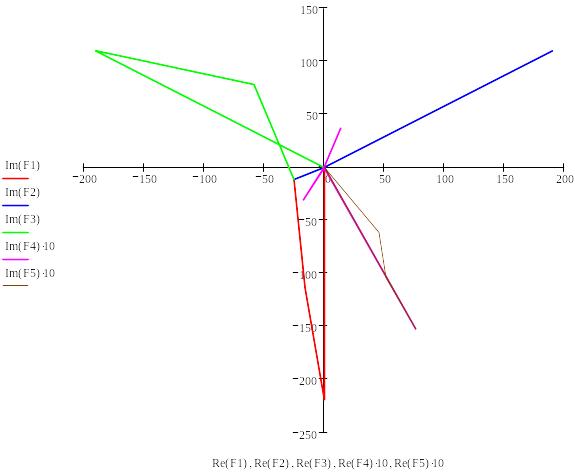
Построенный график рекомендуется скопировать в графический редактор, например, в Microsoft Visio и проставить индексы узлов и направления стрелок векторов токов и напряжений.