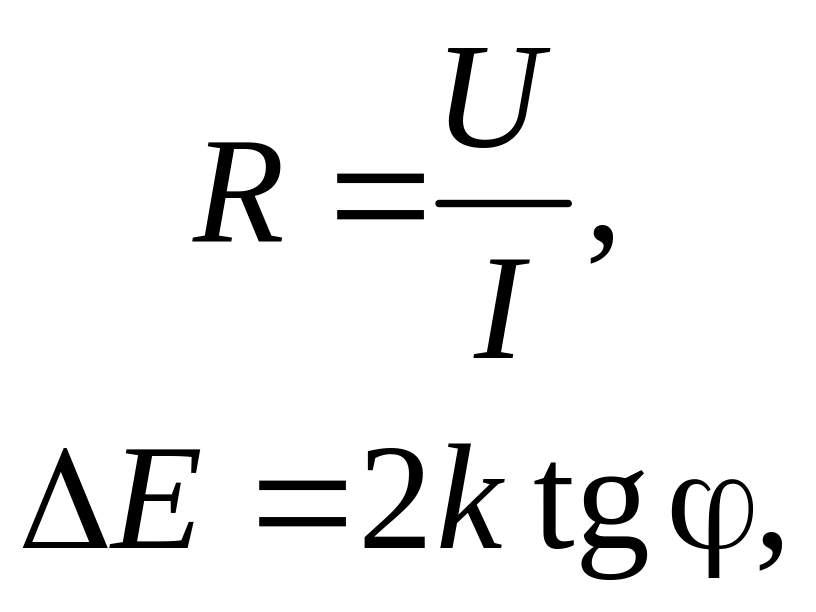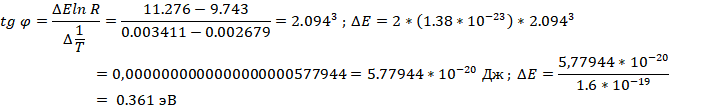Оптика 3 семак / Грязнова / ЛБ-3 Кшинин И 1Б92
.docЛабораторная работа Э–09 Изучение температурной зависимости сопротивления полупроводников и определение энергии активации проводимости
Отчёт о работе
Работу выполнил: |
|
фамилия |
Кшинин |
имя |
Иван |
отчество |
Бахтиёрович |
группа |
1Б92 |
Краткое теоретическое содержание работы
Энергия активации проводимости — это ... |
Энергия необходимая для создания носителей заряда, или энергия, которую нужно затратить чтобы перевести электрон из валентной зоны в зону проводимости. |
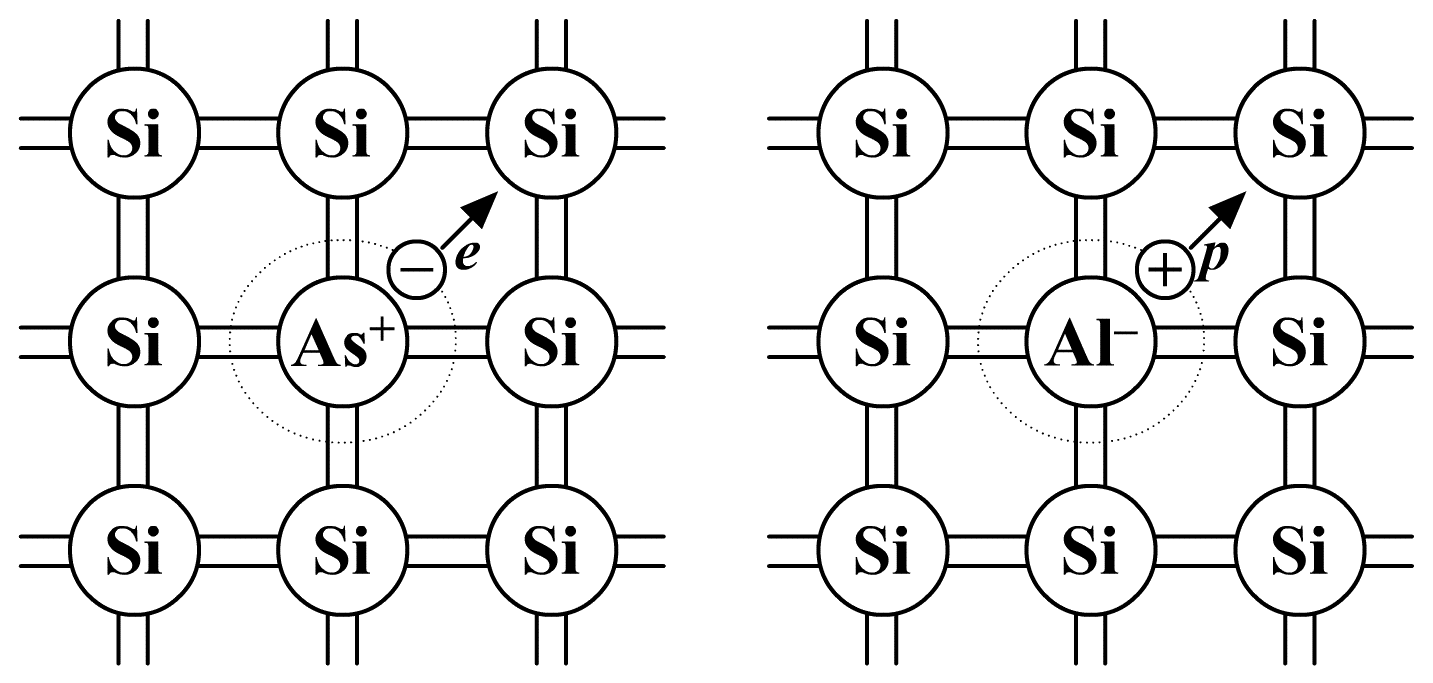
Существуют полупроводники n-типа и p-типа, схематично представленные на рисунке
Роль примеси в проводнике n-типа: |
Сама примесь в полупроводнике используется для увеличения числа носителей заряда, плюса или минуса. Они бывают донорные и акцепторные.
В полупроводнике n типа при повышении температуры электрон будет оторван от примеси и может свободно перемещаться по кристаллу, а по типу примеси донорная. Если сказать по-другому, то: донорные примеси — это примеси, которые поставляют электроны проводимости без возникновения равного количества подвижных дырок. |
Роль примеси в проводнике p-типа: |
С примесью типа акцепторной, образуется свободная дырка, перемещающаяся со связями и принимающая участие в проводимости кристалла. |
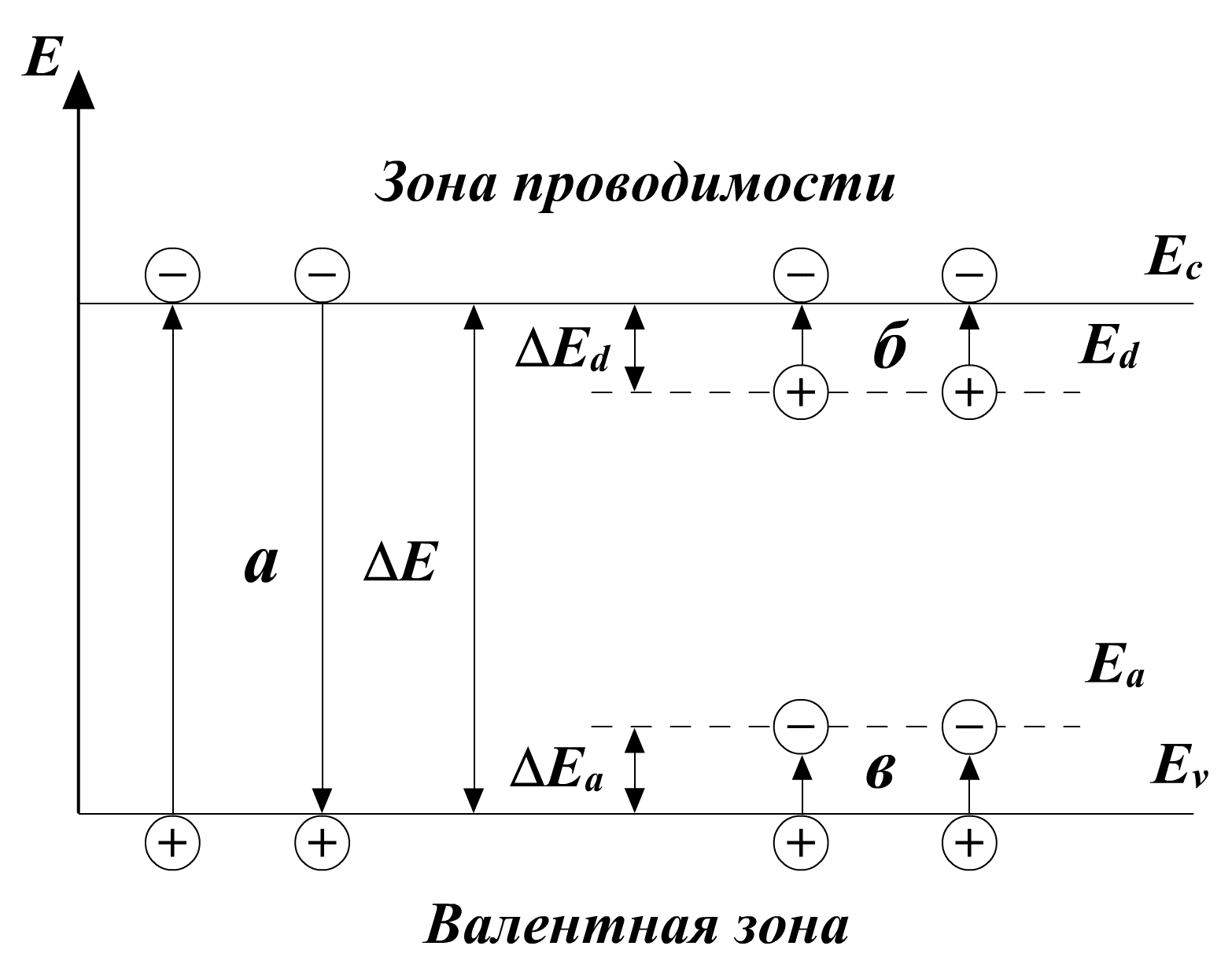
На эмпирической диаграмме |
||
|
Ec — |
Дно зоны проводимости |
Ev — |
Потолок валентной зоны |
|
Ea — |
Энергетический уровень |
|
Ed — |
Энергетические уровень |
|
ΔE — |
Соответствующие энергии активации |
|
ΔEa — |
Энергия активации, а |
|
ΔEd — |
Энергия активации д |
|
Сопротивление полупроводника уменьшается с ростом температуры согласно уравнению: |
||
R = |
|
|
где |
||
R0 — |
Постоянная величина полупроводника |
|
ΔE — |
Энергия |
|
k — |
Постоянная Больцмана (К->k) |
|
T — |
Абсолютная температура |
|
Если построить
зависимость ln Rот
|
Прямой |
, |
||
из которой определяют значение |
Энергии активации |
. |
||
Расчётные формулы
|
где |
U — |
Напряжение |
I — |
Ток |
||
k — |
Постоянная Больцмана |
||
tg φ — |
Тангенс угла к прямой оси абсцисс |
||
ΔE — |
Энергия |
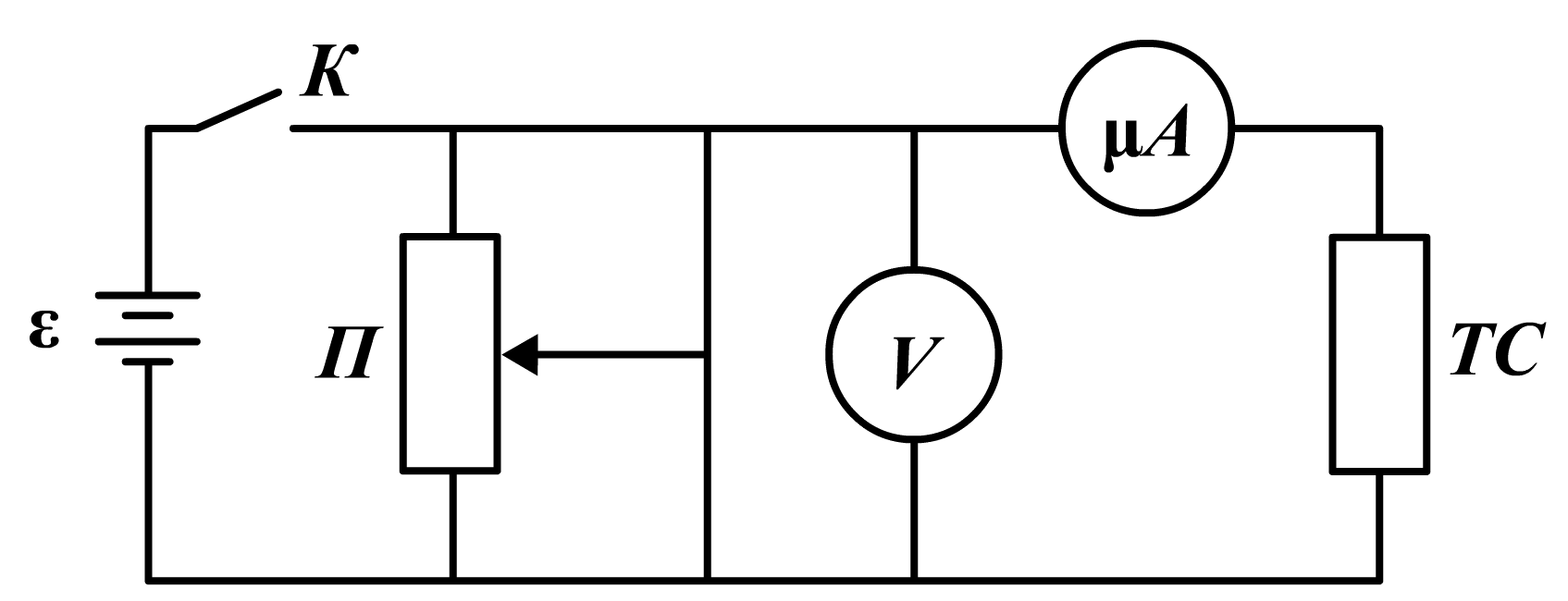
Схема установки
|
Обозначения |
|
П — |
Потенциометр |
|
ТС — |
Термистор- переменное сопротивления |
|
V — |
Вольтметр |
|
μA — |
Микроамперметр |
|
K — |
Кнопка- переключатель |
|
ε — |
Источник тока |
|
Результаты измерений
Таблица 1
U (В) |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
5 |
5.5 |
6 |
6.5 |
7 |
I (A), 10–5 |
6 |
13 |
19 |
24 |
31 |
38 |
45 |
52 |
60 |
68 |
75 |
84 |
92 |
99 |
Таблица 2
t, °C |
T, K |
, K |
I (A) |
U (В) |
R (Ом) |
ln R |
20 |
293,15 |
0,003411 |
0.000019 |
1.5 |
78947 |
11,276 |
25 |
298,15 |
0,003354 |
0.000021 |
1.5 |
71429 |
11,176 |
30 |
303,15 |
0,003298 |
0.000024 |
1.5 |
62500 |
11,042 |
35 |
308,15 |
0,003245 |
0.000027 |
1.5 |
55555 |
10,925 |
40 |
313,15 |
0,003193 |
0.000030 |
1.5 |
50000 |
10,819 |
45 |
318,15 |
0,003143 |
0.000033 |
1.5 |
45454 |
10,724 |
50 |
323,15 |
0,003094 |
0.000037 |
1.5 |
40540 |
10,610 |
55 |
328,15 |
0,003047 |
0.000040 |
1.5 |
37500 |
10,532 |
60 |
333,15 |
0,003001 |
0.000044 |
1.5 |
34090 |
10,436 |
65 |
338,15 |
0,002957 |
0.000049 |
1.5 |
30612 |
10,329 |
70 |
343,15 |
0,002914 |
0.000053 |
1.5 |
28301 |
10,250 |
75 |
348,15 |
0,002872 |
0.000059 |
1.5 |
25423 |
10,143 |
80 |
353,15 |
0,002831 |
0.000064 |
1.5 |
23437 |
10,062 |
85 |
358,15 |
0,002792 |
0.000069 |
1.5 |
21739 |
9,986 |
90 |
363,15 |
0,002753 |
0.000075 |
1.5 |
20000 |
9,903 |
95 |
368,15 |
0,002716 |
0.000080 |
1.5 |
18750 |
9,838 |
100 |
373,15 |
0,002679 |
0.000088 |
1.5 |
17045 |
9,743 |
Обработка результатов
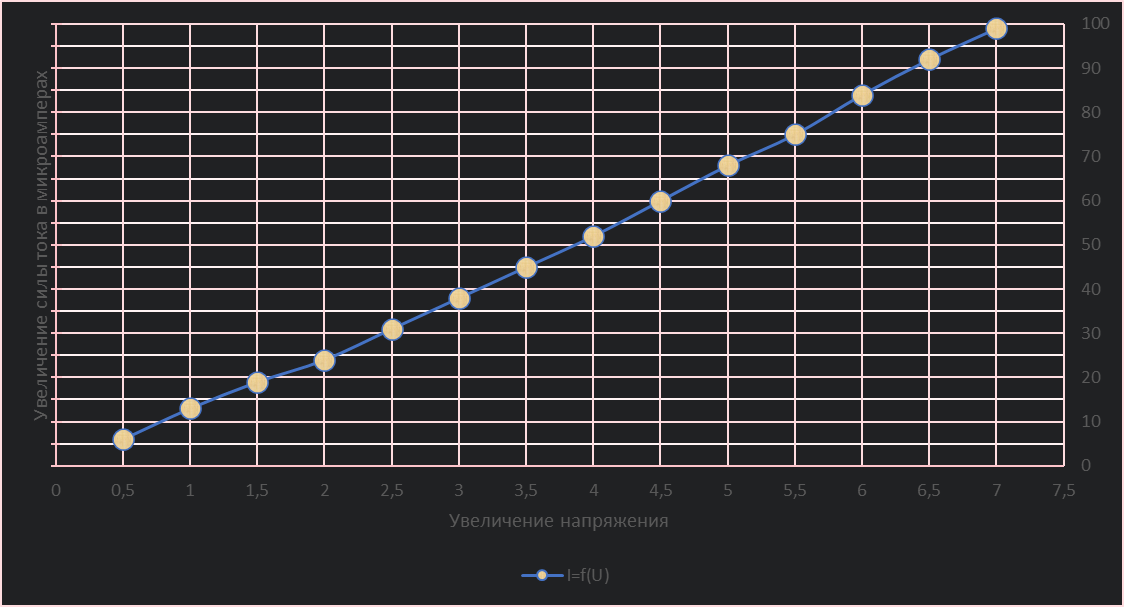
1. По данным таблицы 1 строим вольтамперную характеристику полупроводника при комнатной температуре.
График зависимости I = f(U)
|
Выводы |
С увеличением значения напряжения увеличивается сила тока, проходящая по проводнику. |
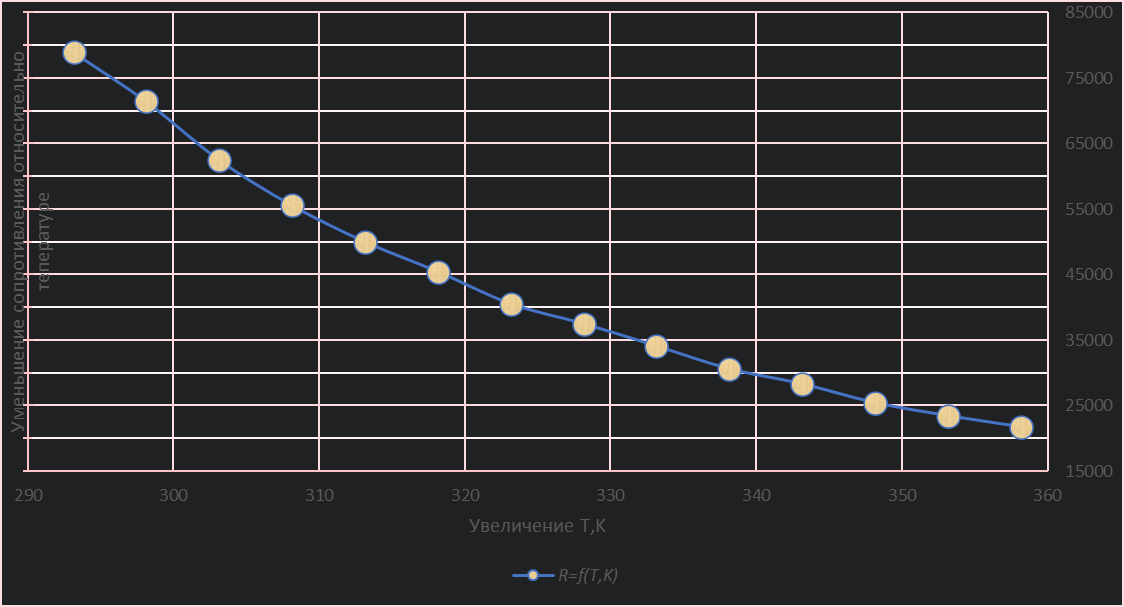
2. Строим график температурной зависимости сопротивления по таблице 2.
График зависимости R = f(T)
|
Выводы |
С увеличением температуры сопротивление уменьшается |
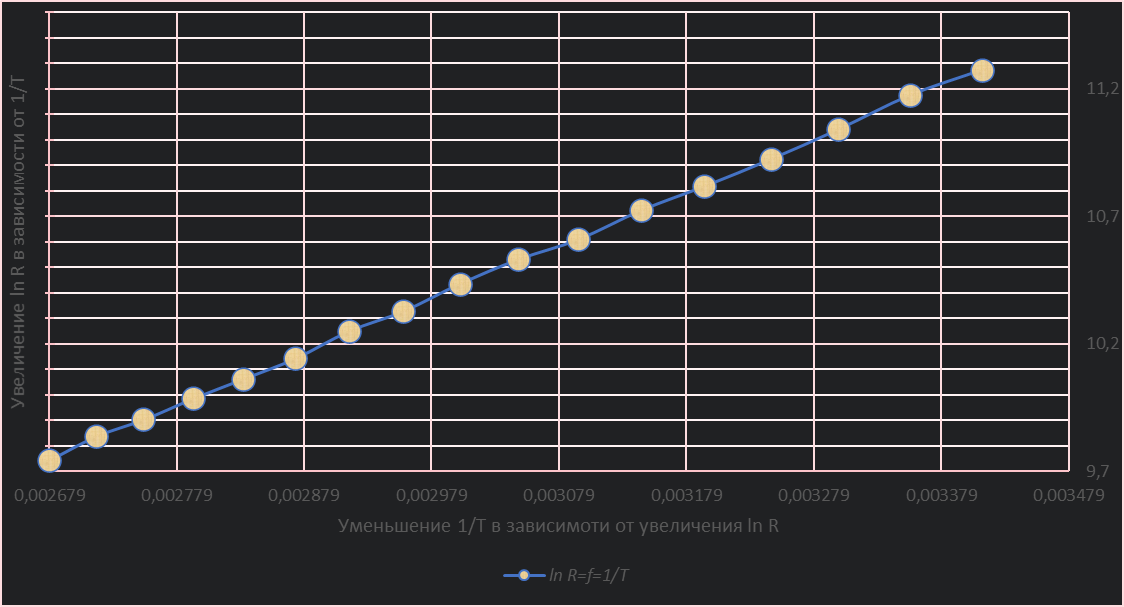
3. Строим график зависимости логарифма сопротивления от величины, обратной температуре, по таблице 2.
График зависимости
![]()
|
Выводы |
Через график можно найти
|
Вывод
Экспериментальным путем доказали зависимость сопротивления от температуры и тока от напряжения. Построили графики их зависимостей. И определили энергию активации проводимости:
P.S
Графики грубые (ибо, к сожалению, при более детальном графике он не влезет в окно, а цифры будут ложиться друг на друга) Также
возможно неправильно выведен логарифм
сопротивления!?Я взял обычный натуральный
логарифм. Возможно, и у остальных
также, так как R0
у нас нигде не дан в условиях и по
формуле его не выяснить:
Далее, из – за того что не понятно вольтметр в установке или милливольтметр он был принят мной как вольтметр, ибо его так обозвали в задании, а на практике он не выглядел так(Обычно они помечаются mV или V, kV на задней стороне но нам ее никто не показывал, или спереди под шкалой) а из за маркировки 75 mV он заставил подумать над тем кто он такой mV или V, а из-за этого пришлось бы домножать силу тока на 1000. |