КОСОЙ ИЗГИБ СТЕРЖНЯ

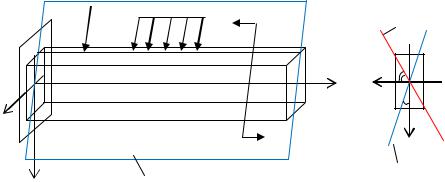
КОСОЙ ИЗГИБ СТЕРЖНЯ

1. Расчет на прочность балок при косом изгибе. Основные понятия

Косой изгиб реализуется, если все нагрузки, приложенные к балке, перпендикулярны ее оси и лежат в одной плоскости, которая проходит через ось стержня и не содержит в себе ни одну из главных центральных осей поперечного сечения (рис. 1). В этом случае в поперечном сечении стержня отличны от нуля четыре внутренних усилия: поперечные силы Qx, Qy и изгибающие моменты Mx, My.

В расчетах на прочность и жесткость поперечными силами, как правило, пренебрегают. Изгибающие моменты выражают через изгибающий момент в силовой плоскости:

где M – изгибающий момент в силовой плоскости; α – угол между осью y и силовой линией.

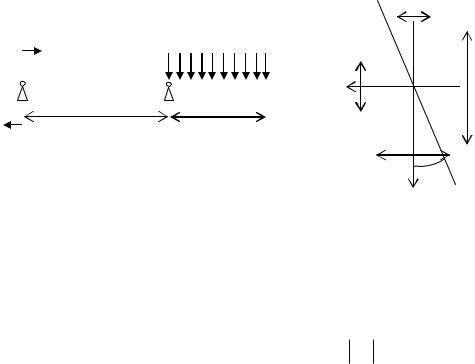
В выбранной системе координат (рис. 1) угол α положительный, если откладывается от оси y против часовой стрелки. На рис. 2 показаны положительные углы для разного направления осей координат.

Нормальные напряжения при косом изгибе вычисляются по формуле:

Рис. 2

Максимального по модулю значения нормальные напряжения достигают в точках, наиболее удаленных от нейтральной оси. Нейтральная ось – это линия в поперечном сечении, на которой нормальные напряжения равны нулю. Уравнение нейтральной оси имеет вид:

Нейтральная ось проходит через начало координат и делит поперечное сечение балки на сжатую и растянутую области.

Угол наклона нейтральной оси к оси x можно найти из соотношения:

Угол откладывается от оси x в том же направлении, что и угол откладывался от оси y.

Условие прочности при косом изгибе имеет вид:

где xоп, yоп – координаты точки, наиболее удаленной от нейтральной оси. Если поперечное сечение можно вписать в прямоугольник так, чтобы

угловые точки сечения совпадали с угловыми точками прямоугольника, то условие прочности можно записать в виде:

2. Подбор сечения балки при косом изгибе

Для заданной балки (рис. 3) от нагрузки, действующей в плоскости, отклоненной от вертикали на угол α, необходимо:

1.Построить полную эпюру изгибающих моментов в плоскости действия сил.

2.Подобрать размеры поперечного сечения, приняв [σ] = 20 МПа.

3.Определить положение нейтральной оси.

4.В опасном сечении построить эпюру нормального напряжения.

В расчете примем a = 3 м, b = 2 м, m = 30 кНм, q = 10 кН/м, α = 30°.

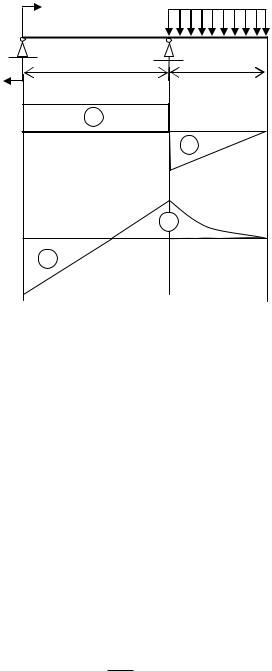
Эпюры поперечной силы и изгибающего момента в силовой плоскости представлены на рис. 4.

Из эпюры изгибающего момента M определяем, что опасным

является сечение над левой опорой, где M M max 30 кН·м.

Поскольку сечение можно вписать в прямоугольник так, чтобы угловые точки сечения совпадали с угловыми точками прямоугольника, используем условие прочности (6), записав его в виде:

kWx 1,3,

Wy

где xmax 1, 5c, ymax 2c .

Подставим найденные значения в формулу (7) и вычислим параметр c:

поперечного сечения.

Запишем уравнение нейтральной оси и вычислим угол :

Для построения нейтральной оси угол φ откладываем от оси x в ту же сторону, в которую откладывается угол α от оси y, т. е. против часовой стрелки, проводим прямую линию через начало координат (рис. 5).

Эпюра нормальных напряжений строится на отрезке, перпендикулярном к нейтральной оси (отрезок AB на рис. 5). Через наиболее удаленные от нейтральной оси точки сечения проводят линии, параллельные нейтральной оси. В произвольном масштабе откладывают отрезок AA1, определяющий напряжение в точке 1, через точку A1 и ноль на нейтральной оси проводят прямую линию A1B1. Отрезок BB1 соответствует напряжению в точке 2.

н.о. y

+B

B1 20

Рис. 5

Численные значения напряжений определим по формуле (2).

Координаты точки 1: x(1) = 1,5c, y(1) = –2c; координаты точки 2: x(2) = –1,5c, y(2) = c. Тогда

Поскольку сечение имеет две оси симметрии, то напряжения в точках 1 и 2 получились равными по модулю, но противоположными по знаку.