МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Факультет электроники Кафедра радиотехнической электроники

"Применение информационных технологий для решения инженерной задачи "

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовой работе по дисциплине "Информатика"

Доцент, к.т.н. А.С.Иванов

Студент гр.2211 Ю.В.Тимофеев

Санкт-Петербург 2003

СОДЕРЖАНИЕ

стр.

1. Постановка задачи и метод решения 3

2. Текст программы 4

3. Листинг результатов 6

4. Диаграмма 7

5. Заключение 8

Microsoft, MS являются зарегистрированными товарными знаками корпорации Microsoft, а Microsoft Works является торговым знаком корпорации Microsoft в США и других странах.

 Microsoft Corporation

1. Постановка задачи

Математическая модель задачи описывается двумя переменными величинами Х и Y, связанными между собой системой двух трансцендентных уравнений вида:

Y=COS(X/P) Y=SQRT(P*X),

где P=Ng/(Ng+Ns) – параметр системы; Ng – номер учебной группы; Ns – номер студента в группе.

Искомые значения переменных величин являются корнями системы уравнений и зависят также от значения параметра Р. Для решения задачи необходимо с заданной погрешностью eps=0,0001 определить корни системы уравнений.

Решение системы трансцендентных уравнений производится численно методом деления пополам корневого отрезка, содержащего корень Х. Исходные границы корневого отрезка X1, X2 находятся путем вычисления значений функций обоих уравнений для заданных значений аргумента с фиксированным шагом dX=0,1. Для каждого значения Х вычисляется разница значений функций обоих уравнений – dY. Два соседних знакопеременных значения dY1 и dY2 определяют соответствующие им X1 и X2.

Основная процедура заключается в том, что корневой отрезок делится пополам, находится значение Хс в средней точке и затем вычисляется соответствующее ему значение dYc. Абсолютная величина полученного значения сравнивается с заданной погрешностью eps=0,001 и в случае, когда abs(dYc) < eps, полученные значения Хс и Yc принимаются в качестве корней системы уравнений.

В случае, когда abs(dYc) > eps, dYc сравнивается с значениями dY1 и dY2 и из них выбирается то, которое отличается знаком от dYc. Одной из границ нового корневого отрезка становится значение Хс, другой либо Х1, либо Х2. Далее повторяется основная процедура до получения корней системы уравнений.

Количество повторов (шагов) основной процедуры зависит от заданной величины погрешности. Дополнительно исследуется зависимость количества шагов от значений погрешности eps=1.E-5 и eps=1.E-6.

2. Текст программы

%Y1=COS(X/P)%Y2=SQRT(P*X)

%P=Ng/(Ng+Ns)

Ng=2211; %номер группы

Ns=22 %номер студента;

P=Ng/(Ng+Ns); %параметр системы;

%eps=1.E-5

%eps=1.E-6

eps=0.0001; %значение погрешности

dx=0.1;

x=0;

dY=1;

%нахождение корневого;

i=0; %отрезка.

while dY>0;

i=i+1;

xt(i)=x;

Y1=cos(x/P);

Y2=sqrt(P*x);

yt1(i)=Y1;

yt2(i)=Y2;

dY=Y1-Y2;

x=x+dx;

end;

%данные для графика;

y1r(1)=yt1(i);

y1r(2)=yt1(i-1);

y2r(1)=yt2(i);

y2r(2)=yt2(i-1);

xr(1)=xt(i-1);

xr(2)=xt(i);

for n=1:2, xrt(n)=xr(n)

end;

%вычисление корней c

j=1; %учетом погрешности;

while abs(dY)>eps; %(основная процедура)

xc=(xr(1)+xr(2))/2;

Y1=cos(xc/P);

Y2=sqrt(P*xc);

dY=Y1-Y2;

if dY>0 xr(1)=xc;

else xr(2)=xc;

end;

j=j+1;

end;

%вывод ответов

disp('Исходные данные'); disp('Ng='); %на монитор

disp(Ng);

disp('Ns='); disp(Ns);

disp('P='); disp(P);

disp('xc='); disp(xc);

disp('Y1='); disp(Y1);

disp('Y2='); disp(Y2);

disp('Шагов='); disp(j);

plot(xrt,y1r,xrt,y2r);

3. Листинг результатов

3.1. eps=0.0001

Исходные данные

Ng=2211

Ns=22

P=0.9901

xc=0.6418

Y1=0.7972

Y2=0.7972

Шагов=9

3.2. eps=0.00001

Исходные данные

Ng=2211

Ns=22

P=0.9901

xc=0.6418

Y1=0.7972

Y2=0.7972

Шагов=14

3.3. eps=0.000001

Исходные данные

Ng=2211

Ns=22

P=0.9901

xc=0.6418

Y1=0.7972

Y2=0.7972

Шагов=17

Таблица 1. Зависимость числа шагов от логарифма погрешности

	eps=0.0001	eps=0.00001	eps=0.000001
Log(eps)	-4	-5	-6
Число шагов	9	14	17

4. Д 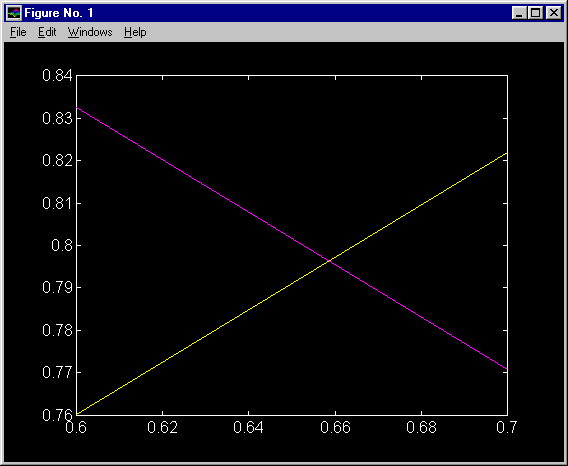иаграмма

Рис. Графическая иллюстрация корней системы уравнений

4. Заключение

Анализирую экспериментально полученные данные по зависимости числа шагов от логарифма погрешности можно сделать заключение, что с уменьшением значения логарифма погрешности, количество шагов основной процедуры, монотонно увеличивается.

8