Расчетная часть Условия задачи:
1
.
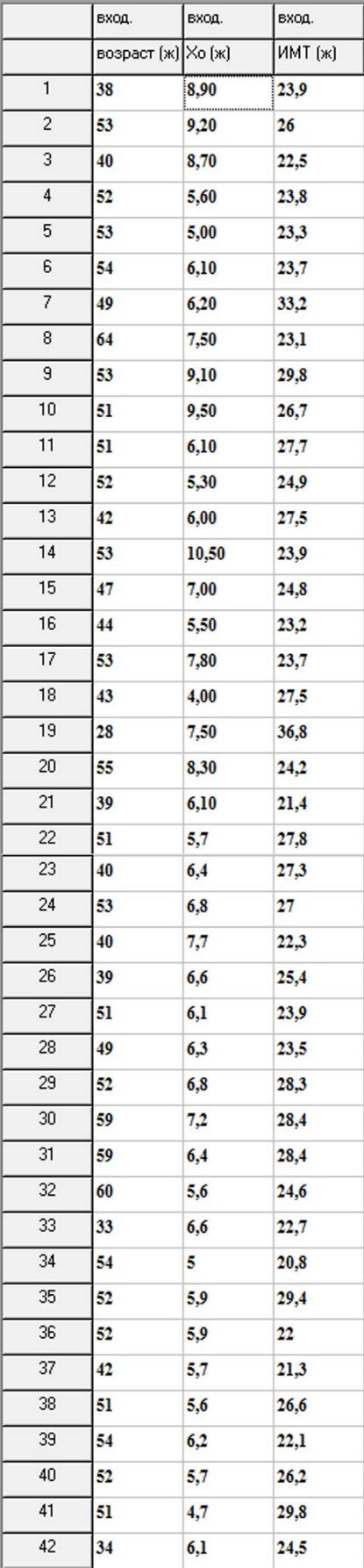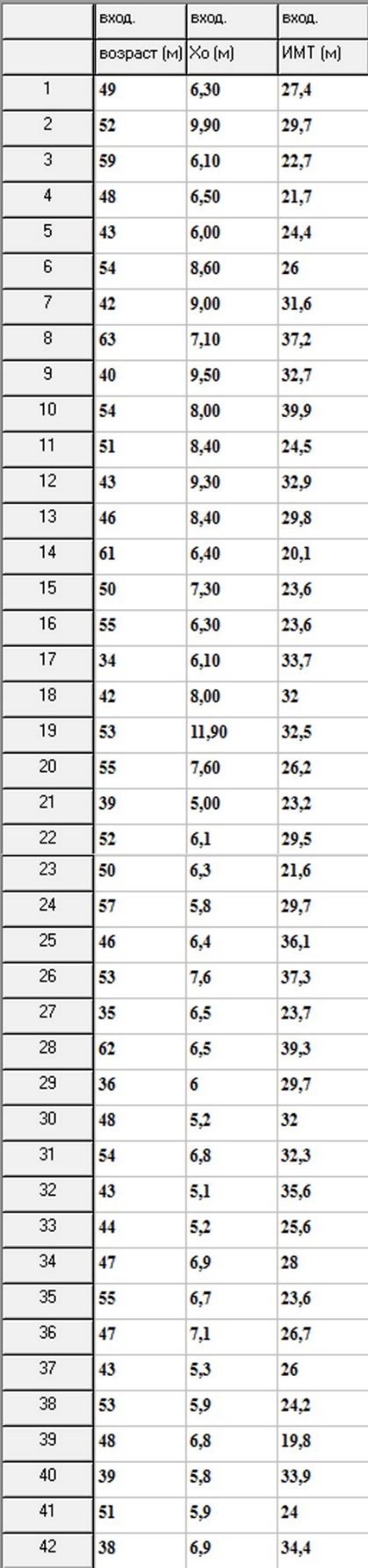
Строим вариационные ряды на основе
предоставленных данных
В
программе «StatMed»
создаем таблицу и вводим данные для
показателей возраст, Хо и ИМТ отдельно
для 1 группы (женщины) и для 2 группы
(мужчины).
Вариационный ряд для
показателей для каждой группы состоит
из 3х колонок и 42 строк. Все данные
приведены выше в таблице.
2. Выполняем проверку на нормальность
1 Группа (женщины)
Переменная возраст (ж)
Критерий хи-квадрат проверки распределения на нормальность
Объем выборки N=42. Число степеней свободы k=4. Chi-square=23,200, уровень значимости p=<0,001
Распределение отличается от нормального на уровне значимости p=<0,001
Переменная Хо (ж)
Критерий хи-квадрат проверки распределения на нормальность
Объем выборки N=42. Число степеней свободы k=6. Chi-square=12,300, уровень значимости p=0,056
Распределение не отличается от нормального на уровне значимости, p=0,056
Переменная ИМТ (ж)
Критерий хи-квадрат проверки распределения на нормальность
Объем выборки N=42. Число степеней свободы k=5. Chi-square=8,420, уровень значимости p=0,135
Распределение не отличается от нормального на уровне значимости, p=0,135 Вывод: Распределение по показателям возраст, Хо, ИМТ у женщин с АГ в большинстве не отличается от нормального.
2 Группа (мужчины)
Переменная возраст (м)
Критерий хи-квадрат проверки распределения на нормальность
Объем выборки N=42. Число степеней свободы k=5. Chi-square=3,430, уровень значимости p=0,633
Распределение не отличается от нормального на уровне значимости, p=0,633
Переменная Хо (м)
Критерий хи-квадрат проверки распределения на нормальность
Объем выборки N=42. Число степеней свободы k=6. Chi-square=7,730, уровень значимости p=0,258
Распределение не отличается от нормального на уровне значимости, p=0,258
Переменная ИМТ (м)
Критерий хи-квадрат проверки распределения на нормальность
Объем выборки N=42. Число степеней свободы k=4. Chi-square=7,460, уровень значимости p=0,114
Распределение не отличается от нормального на уровне значимости, p=0,114 Вывод: Распределение по показателям возраст, Хо, ИМТ у мужчин с АГ не отличается от нормального.
3. Проводим расчет описательной статистики
1 группа (женщины)
Рассмотрим таблицу:
Рассмотрим доверительный интервал:
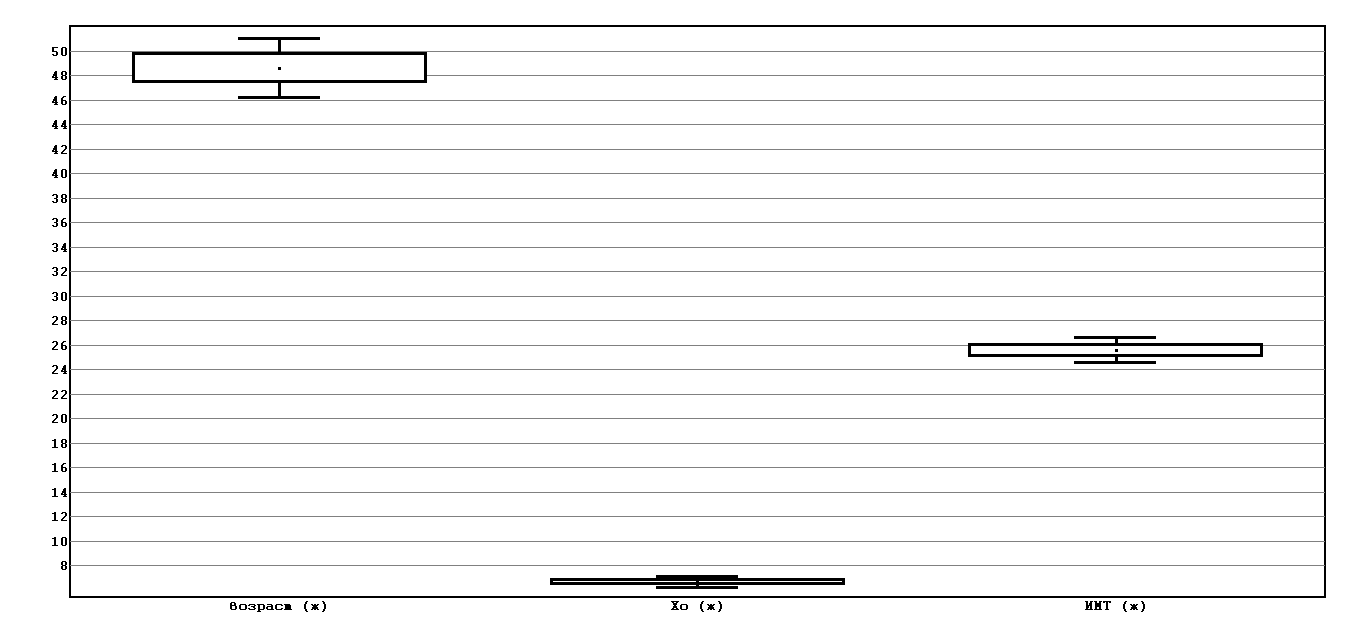
Рассмотрим график:
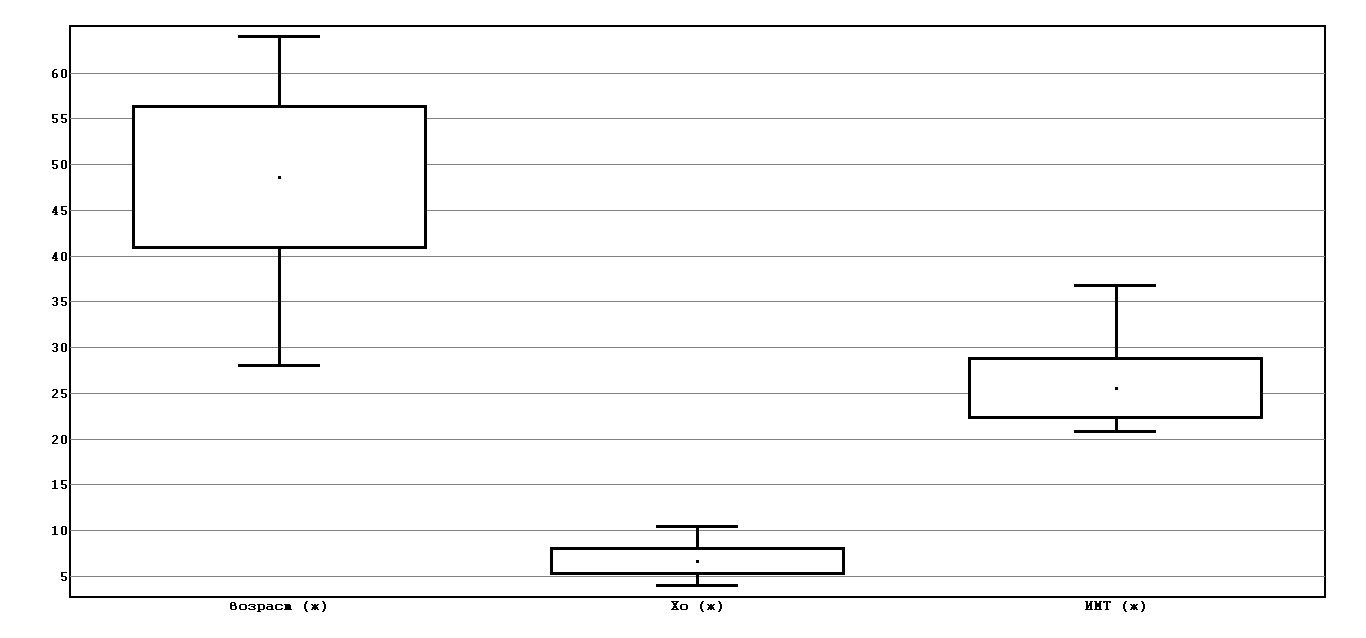
2 группа (мужчины)
Рассмотрим таблицу:
Рассмотрим доверительный интервал:
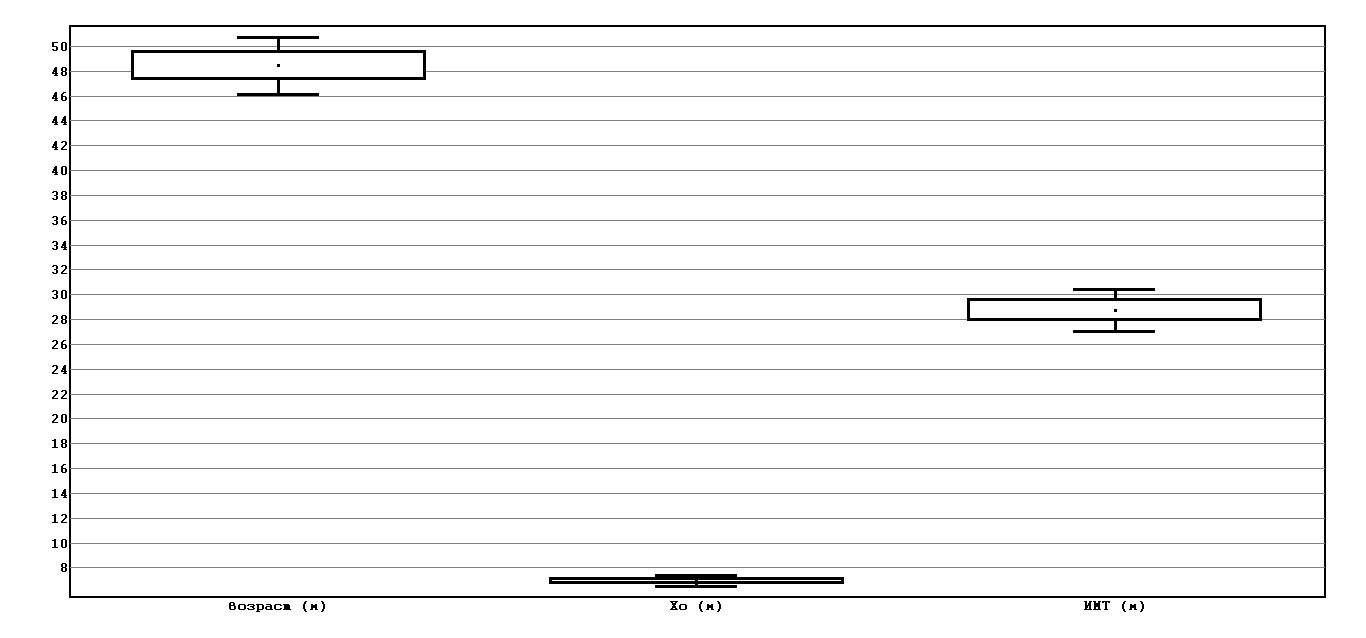
Рассмотрим график:
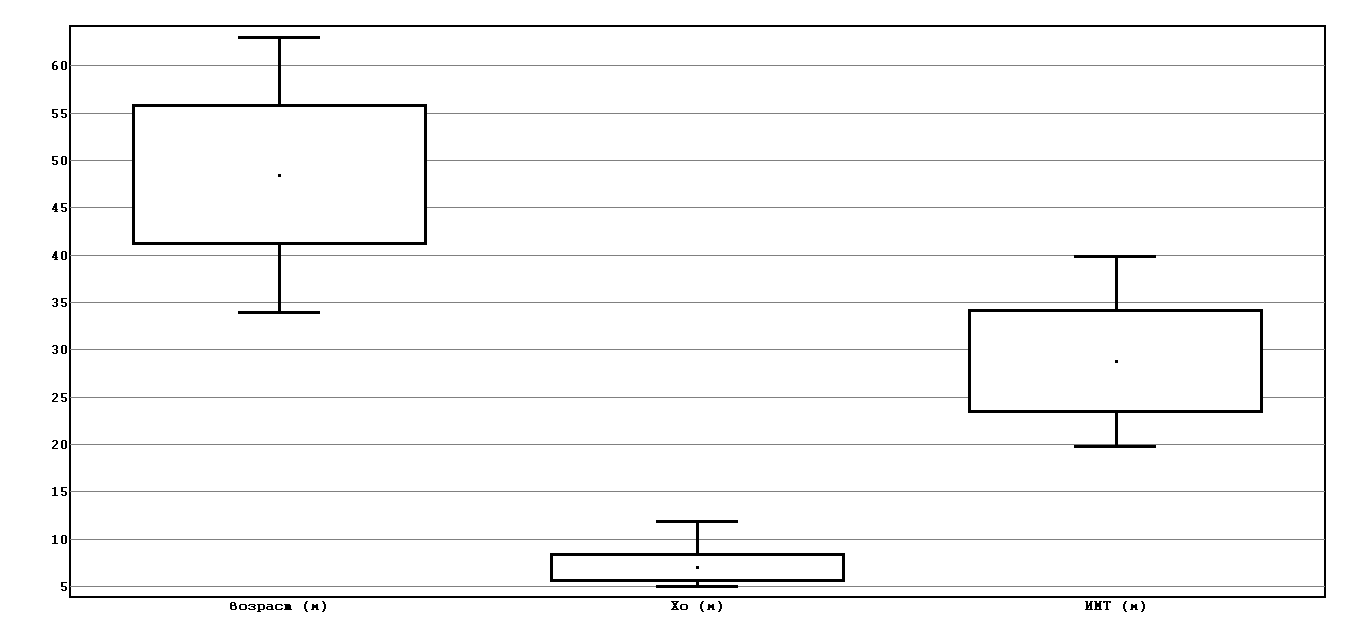
4. Построим гистограммы
1 группа (женщины)
а) возраст
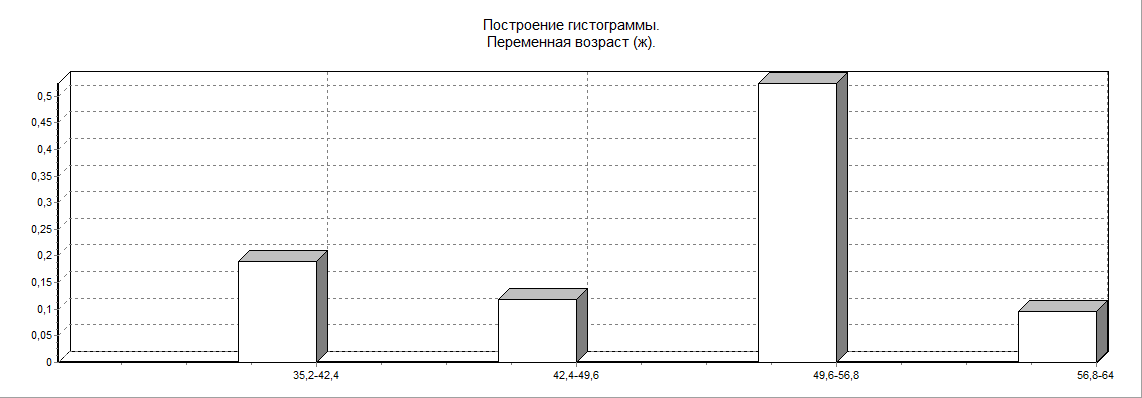
б) Хо (уровень холестерина)
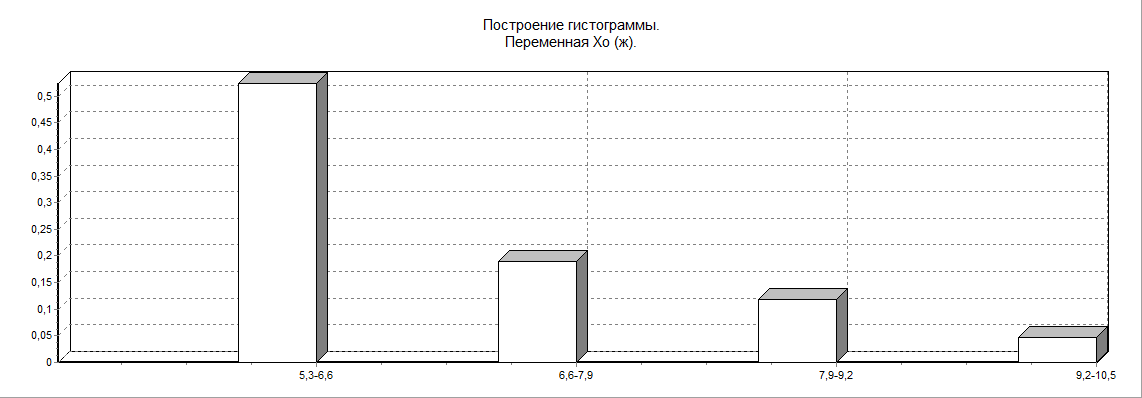
в) ИМТ (индекс массы тела)
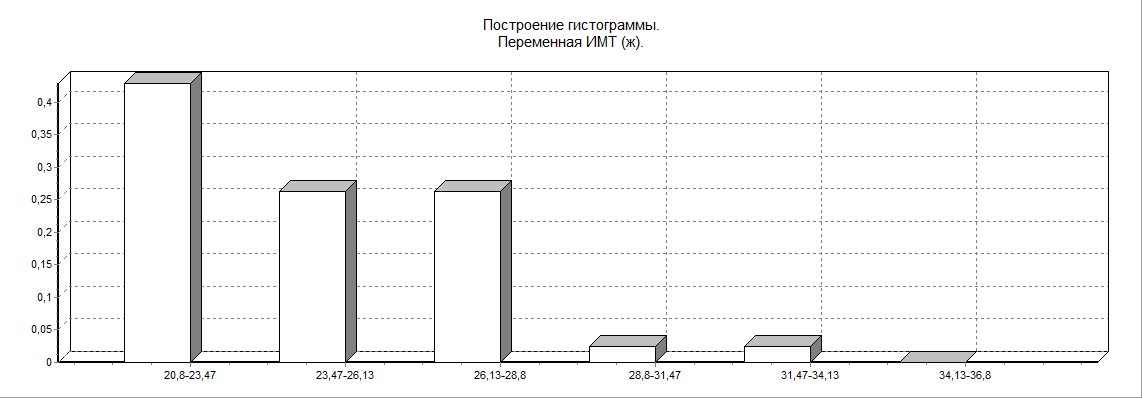
2 группа (мужчины)
а) возраст
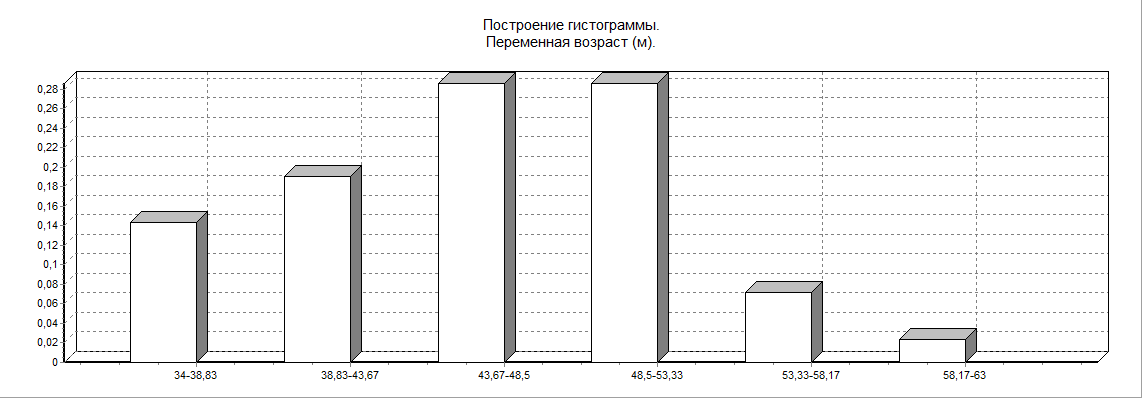
б) Хо (уровень холестерина)
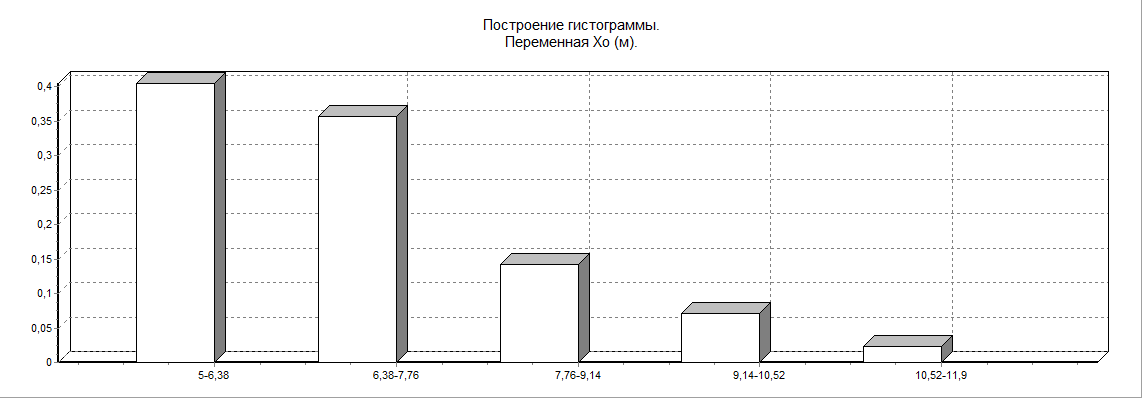
в) ИМТ (индекс массы тела)
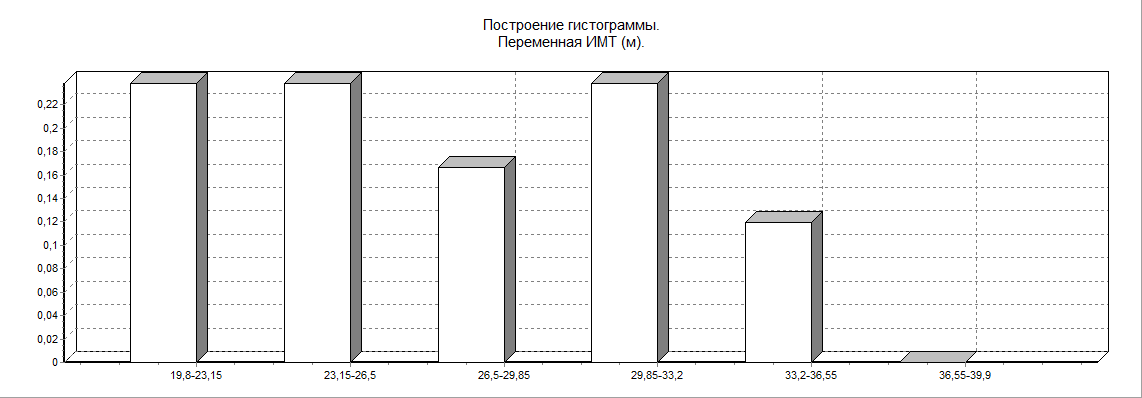
5. Проведем расчет линейного коэффициента корреляции Пирсона
Так как распределение случайных величин не отличается от нормального, применяем коэффициент корреляции Пирсона.
1 группа (женщины)
Проверка значимости линейной корреляционной связи для двух выборок. Коэффициент корреляции Пирсона.
Переменные: Хо (ж), ИМТ (ж).
Объем выборки: N=42.
R=0,025, число степеней свободы k=40.
Линейная корреляционная связь отсутствует, R=0, p=0,874.
Вывод: Хо и ИМТ не имеет линейной корреляционной связи. Среднее значение переменных отличаются на уровне значимости р<0,001.
2 группа (мужчины)
Проверка значимости линейной корреляционной связи для двух выборок. Коэффициент корреляции Пирсона.
Переменные: Хо (м), ИМТ (м).
Объем выборки: N=42.
R=0,238, число степеней свободы k=40.
Линейная корреляционная связь отсутствует, R=0, p=0,129.
Вывод: Хо и ИМТ не имеет линейной корреляционной связи. Среднее значение переменных отличаются на уровне значимости р<0,001.
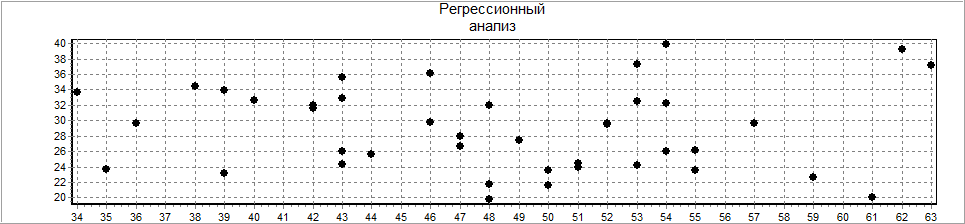
6. Определим зависимость массы тела от возраста 1 группа (женщины)
Построение линейной модели.
Зависимость переменной ИМТ (м) от переменной возраст (м).
Объем выборки: N=42.
Коэффициент линейной корреляции R= -0,049, число степеней свободы m,k= 1,40.
Модель не адекватна, F=0,094, уровень значимости p=0,785.
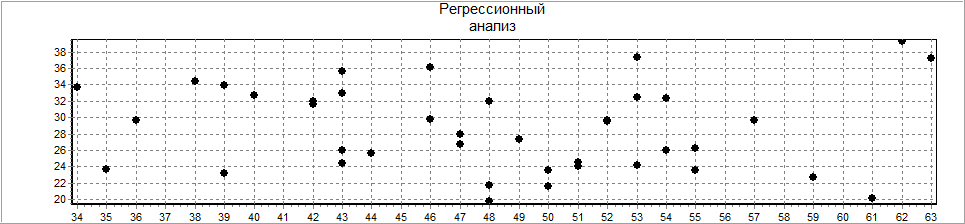
2 группа (мужчины)
Построение линейной модели.
Зависимость переменной ИМТ (м) от переменной возраст (м).
Объем выборки: N=42.
Коэффициент линейной корреляции R= -0,049, число степеней свободы m,k= 1,40.
Модель не адекватна, F=0,094, уровень значимости p=0,785.
Выводы
Знание медицинской статистики, будучи примененным в целях систематического критического анализа медицинских исследований, начинает давать нам новое, более научное понимание того, какие методы лечения полезны и экономически оправданы, а от каких можно отказаться безо всякого ущерба для наших пациентов. Медицинскую практику, основанную на таком новом знании, сегодня называют медициной, основанной на доказательствах. Она обещает повысить одновременно качество и экономическую эффективность медицинской помощи в экономически развитых странах.