
Метод._MathCAD_Prime / Метод._MathCAD_Prime
.pdf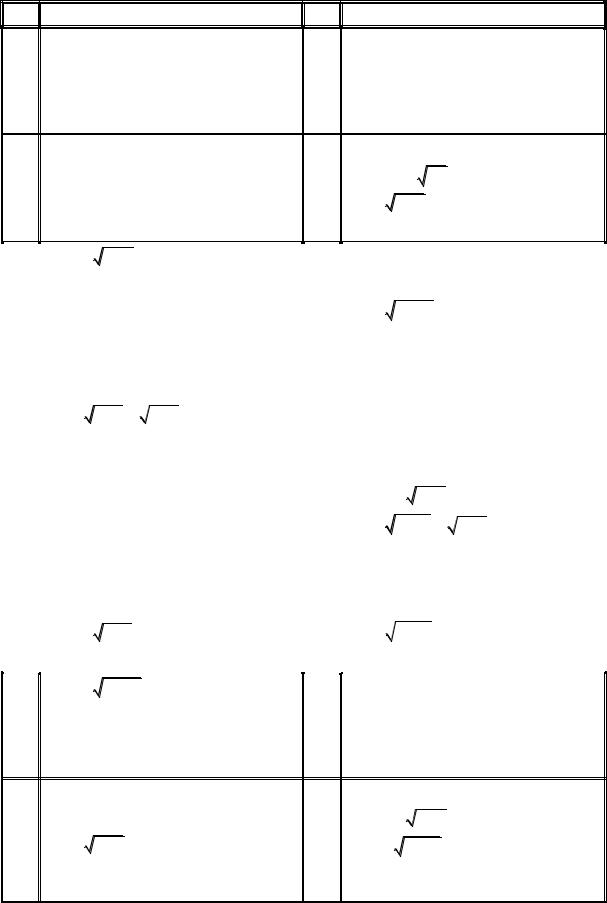
Таблица 3 |
|
|
|
|
|
|
|
|
|
|
|
|
№ |
|
|
|
Функция |
№ |
|
|
|
|
|
Функция |
|
1 |
x2 + ex+3 , если |
− 4 x −2 |
2 |
1,8x2 −1, если − 8 x −2 |
||||||||
|
|
|
2 |
x, если |
−1 x 3 |
|
|
|
2 x |
− 4, если −1 x 2 |
||
|
2 cos |
|
|
e |
|
|||||||
|
y = |
|
|
|
|
|
y = |
|
|
|
|
|
|
lg( x + 5), если |
4 x 6 |
|
ln( x − 6), если x 6 |
||||||||
|
|
|
|
|
|
|
|
|
2 |
+1, |
в остальных случаях |
|
|
2x, в остальных случаях |
|
x |
|
||||||||
3 |
1,5cos 2x +1, если x −5 |
4 |
( x + 2) |
2 |
+1, если x −10 |
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln | x |
− 2 |, если 0 x 2 |
|
3cos | x |, если -5 x 1 |
||||||||
|
y = |
− x+1 |
|
|
|
|
y = |
|
|
|
|
|
|
e |
|
+ 5, если 4 x 6 |
|
3 |
x −1, если 1 x 10 |
||||||
|
|
|
|
в остальных случаях |
|
|
|
|
|
|
|
|
|
x +1, |
|
99, в остальных случаях |
|||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
x 3 |
|
|
|
|
|
|
|
6 |
ex2 |
|
|
|
|
|
|
|
||||||
|
x + 5, если 0< x 4 |
−1, если -1 x 0 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x sin2 ( x −1), если 5 x 12 |
|
ctg( x −1), если 1< x 4 |
||||||||||||||||||||
|
y = |
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lg 5x, если 12 x 22 |
|
|
|
x2 |
+ 2, если 4 x 14 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3x, в остальных случаях |
||||||||||
|
x −1, в остальных случаях |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
cos(3x −1), если − 2 x 1 |
8 |
( x − 4)2 +1, если x −4 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x −1), если -3 x 1 |
||||||
|
ln( x + 5), если 1 x 4 |
|
cos2 |
||||||||||||||||||||
|
y = |
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
x −1 + 3 x +1, если x 10 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
ln( x |
+ 2), если x 1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5x − 7, в остальных случаях |
|
3x, в остальных случаях |
||||||||||||||||||||
9 |
x2 |
+ ln( x +1), если 1 x 4 |
10 |
lg x2 , если − 2 x 0 |
|||||||||||||||||||
|
|
x−4 |
, если 4 x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x +1, если 0 x 4 |
|||||||||||||||||
|
e |
|
|
|
|
|
ctg |
|
|||||||||||||||
|
y = |
|
|
2 |
|
|
|
|
|
|
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|||||
|
sin |
|
|
3x, если 5 x 10 |
|
|
|
+1 + 3 x +1, если x 7 |
|||||||||||||||
|
1,1x −1, в остальных случаях |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
−1, в остальных случаях |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
11 |
1 + sin2 x, если x −3 |
12 |
cos2 |
(2x +1), если − 4 x 2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex−1, если 0 x 4 |
|
lg | 8 − x |, если 9 x 12 |
||||||||||||||||||||
|
y = |
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|||
|
x 5 |
|
x −1, если 4 x 6 |
|
4 |
|
+1, если x 12 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1x, в остальных случаях |
|
0,1x, в остальных случаях |
||||||||||||||||||||
13 |
x |
x2 + 5, если x −7 |
14 |
tg(x +1), если − 2 x 0 |
|||||
|
|
|
|
|
|
|
|
2 |
+1), если 0 x 5 |
|
e1−x , если -5 x 4 |
|
ln(x |
|
|||||
|
y = |
|
|
|
y = |
|
|
|
|
|
cos 3x, если 4 x 6 |
|
3(x − 2)2 + 4, если x 10 |
||||||
|
|
− 4, в остальных случаях |
|
|
|
|
|
|
|
|
x |
|
2, 25x, в остальных случаях |
||||||
15 |
sin2 ( x −1), если -4 x 2 |
16 |
ln | x |, если x −2 |
||||||
|
|
x−4 |
, если 2 x 6 |
|
|
|
|
|
x +1, если 0 x 2 |
|
e |
|
|
ctg |
|
||||
|
y = |
|
|
|
y = |
|
x2 +1, если 5 x 10 |
||
|
3 |
x −1 + x, если 6 x 7 |
|
x |
3 |
||||
|
|
|
|
|
|
2 |
+ 3, в остальных случаях |
||
|
1,11x, в остальных случаях |
|
x |
|
|||||
|
|
|
|
81 |
|
|
|
|
|

Лабораторная работа №7. Программирование циклического вычислительного процесса
Циклическим называется вычислительный процесс, содержащий многократные вычисления по одним и тем же математическим зависимостям, но для различных значений, входящих в него переменных. Количество повторений может задаваться заранее или зависеть от выполнения определенного условия, как в операторе if.
Для составления циклических программ в Mathcad Prime используют операторы и .
1.Оператор цикла с предусловием 
Спомощью оператора  можно реализовать циклический процесс, состоящий из ряда операторов (тело цикла), выполнение которых повторяется до тех пор, пока заданное условие верно, а если условие ложно, то осуществляется выход из оператора цикла. Общий вид:
можно реализовать циклический процесс, состоящий из ряда операторов (тело цикла), выполнение которых повторяется до тех пор, пока заданное условие верно, а если условие ложно, то осуществляется выход из оператора цикла. Общий вид:
принцип работы –
Где, – логическое выражение (условие) – оператор(ы) языка Mathcad Prime (тело цикла),  – истина,
– истина,  –ложь.
–ложь.
Если в цикле необходимо выполнить более одного оператора, то их следует заключить в операторные скобки ( ), т. е. образовать из них составной оператор:
), т. е. образовать из них составной оператор:
82
2. Оператор цикла с параметром 
Оператор  – это оператор цикла с параметром. С помощью оператора for можно реализовать циклический процесс, состоящий из ряда операторов (тело цикла), выполнение которых повторяется до тех пор, пока параметр цикла принадлежит некоторому, заданному диапазону. Параметр цикла – величина, от значения которого зависит количество выполнений операторов, входящих в тело цикла. Тело цикла – оператор или группа операторов, выполнение которых повторяется в зависимости от значения параметра цикла.
– это оператор цикла с параметром. С помощью оператора for можно реализовать циклический процесс, состоящий из ряда операторов (тело цикла), выполнение которых повторяется до тех пор, пока параметр цикла принадлежит некоторому, заданному диапазону. Параметр цикла – величина, от значения которого зависит количество выполнений операторов, входящих в тело цикла. Тело цикла – оператор или группа операторов, выполнение которых повторяется в зависимости от значения параметра цикла.
Общий вид оператора for:
Где,  – любое допустимое имя переменной или параметр цикла, – значение или последовательность значений. Чаще всего – переменнаядиапазон, но можно также использовать вектор или список из скаляров или векторов, задающих последовательность скаляров, которые по очереди становятся значениями переменной . Чтобы выполнить один и тот же расчет над несколькими матрицами, можно определить как последовательность матриц.
– любое допустимое имя переменной или параметр цикла, – значение или последовательность значений. Чаще всего – переменнаядиапазон, но можно также использовать вектор или список из скаляров или векторов, задающих последовательность скаляров, которые по очереди становятся значениями переменной . Чтобы выполнить один и тот же расчет над несколькими матрицами, можно определить как последовательность матриц.  – тело цикла, любое допустимое выражение или последовательность выражений. Допускается, например, локальное назначение или последовательность шагов программы.
– тело цикла, любое допустимое выражение или последовательность выражений. Допускается, например, локальное назначение или последовательность шагов программы.
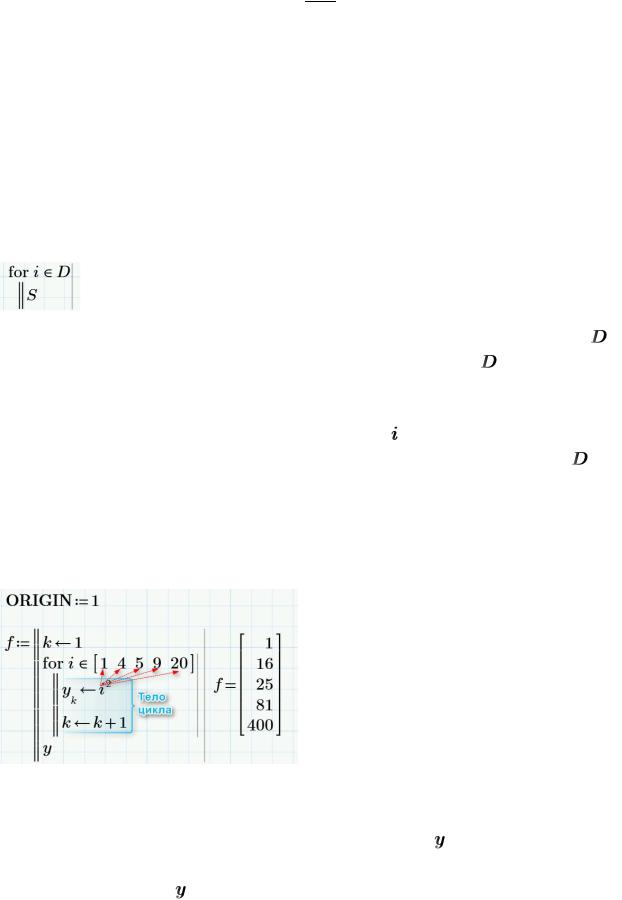
Пример:
Пояснение к программе: Здесь,  – имя программы;
– имя программы;  –параметр цикла, которая поочередно принимает значения элементов заданного вектора. В теле цикла происходит формирование вектора , элементы которого являются квадратами элементов исходного вектора;
–параметр цикла, которая поочередно принимает значения элементов заданного вектора. В теле цикла происходит формирование вектора , элементы которого являются квадратами элементов исходного вектора;  – индексы элементов вектора .
– индексы элементов вектора .
83

Для случая, когда  – переменная-диапазон, в Mathcad Prime предусмотрены две разновидности данного оператора:
– переменная-диапазон, в Mathcad Prime предусмотрены две разновидности данного оператора:
а) обычный оператор цикла с параметром:
Где,  – параметр цикла,
– параметр цикла,  ,
,  – начальное и конечное значения параметра цикла (границы диапазона), – оператор (ы) языка Mathcad Prime или по-другому тело цикла.
– начальное и конечное значения параметра цикла (границы диапазона), – оператор (ы) языка Mathcad Prime или по-другому тело цикла.
Параметр цикла , после каждого выполнения меняется с шагом равным , причем, если начальное значение параметра меньше конечного, то увеличивается на 1. Пример: Найти S =1+ 2 +... + n .
Если начальное значение параметра больше конечного, то уменьшается на 1. Пример: Найти S = n +(n −1) +... +1.
Примечание 1: Диапазон изменения 
 можно набрать на клавиатуре (две точки) или воспользоваться вкладкой Операторы:
можно набрать на клавиатуре (две точки) или воспользоваться вкладкой Операторы:
Примечание 2: Недопустимо, чтобы значение параметра цикла  изменился в результате выполнения оператора , т.е. в теле цикла. В таком случае, оператор, изменяющий значение параметра цикла,
изменился в результате выполнения оператора , т.е. в теле цикла. В таком случае, оператор, изменяющий значение параметра цикла,
84
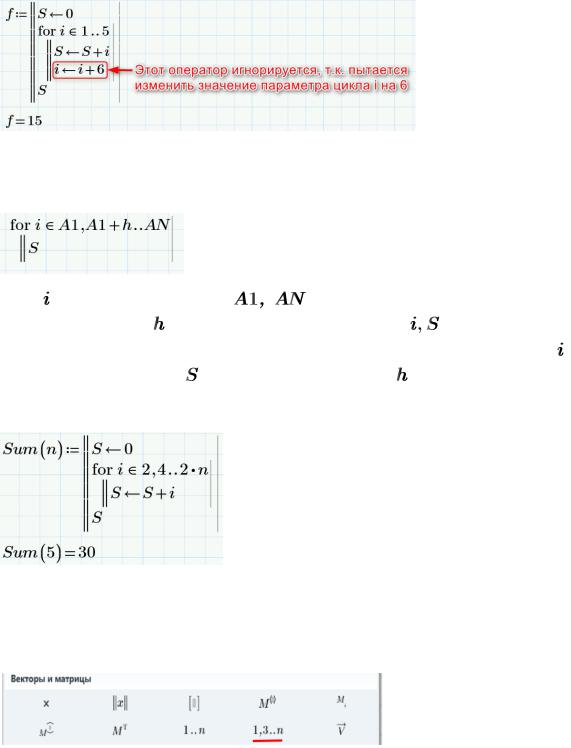
системой Mathcad Prime игнорируется (разумно!). Пример недопустимой организации цикла с параметром:
б) модифицированный оператор цикла с параметром:
Где, – параметр цикла, |
– начальное и конечное значения |
|
параметра цикла, – шаг изменения параметра |
– оператор (ы) языка |
|
Mathcad Prime или по-другому |
тело цикла. |
Параметр цикла , после |
каждого выполнения меняется на величину .
Пример: НайтиS = 2 + 4 +... + 2n .
Примечание: Диапазон изменения 


 можно набрать на клавиатуре (запятая) или воспользоваться вкладкой Операторы:
можно набрать на клавиатуре (запятая) или воспользоваться вкладкой Операторы:
Необходимо отметить, что параметр цикла может принимать не только целое, но и дробное (десятичные и обыкновенные дроби) значение.
85
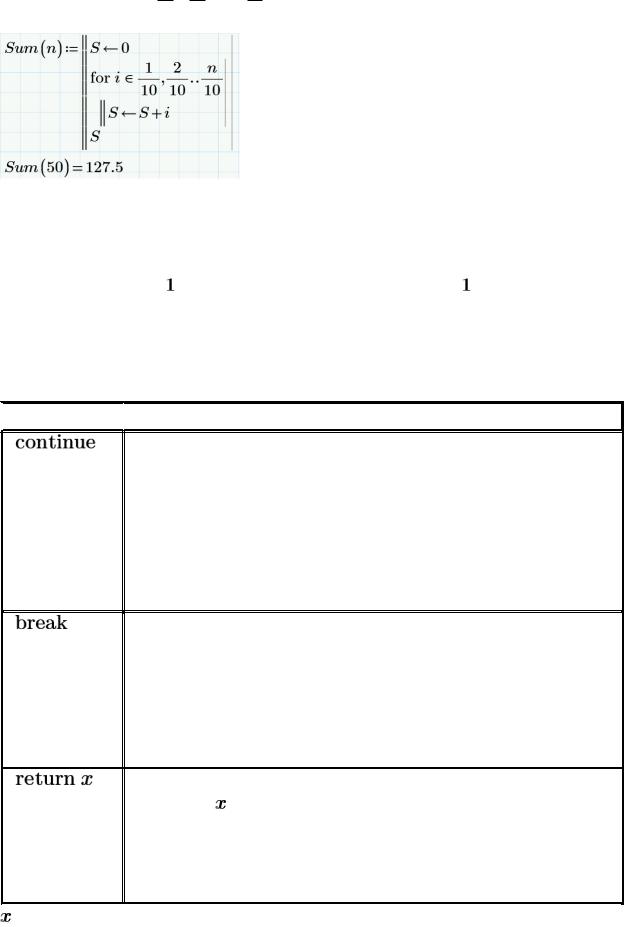
Пример: НайтиS = 101 + 102 +... + 10n .
Главным отличием обычного оператора цикла от модифицированного,
является величина шага изменения параметра. В первом случае этот шаг обязательно равен , а во втором может отличатся от .
Также в Mathcad Prime предусмотрены операторы для пропуска текущей итерации цикла и перехода к следующей, выхода из циклов и программ:


 Оператор
Оператор 

 Описание
Описание
Оставшиеся операторы текущей итерации цикла будут пропущены, а выполнение продолжится с первого оператора цикла. В этом операторе нет аргументов. В цикле  будет увеличено значение переменной итерации.
будет увеличено значение переменной итерации.
В сочетании с условным оператором оператор  позволяет выполнить в программе пропуск текущей итерации и переход к следующей.
позволяет выполнить в программе пропуск текущей итерации и переход к следующей.
Прекращает выполнение текущего цикла и возвращает последнее вычисленное значение. В этом операторе нет аргументов.
В сочетании с условным оператором оператор  позволяет выполнить в программе преждевременный выход из цикла с передачей управления первому оператору, следующему за циклом.
позволяет выполнить в программе преждевременный выход из цикла с передачей управления первому оператору, следующему за циклом.
Прекращает выполнение программы и возвращает значение . Часто используют для отладки программы, при этом Оператор return временно вводится в
программу для проверки значений локальных переменных.
– любое допустимое выражение PTC Mathcad.
86

Примеры:
1. Суммирование нечетных чисел в интервале от до .
Пояснение к программе: Здесь,  – имя программы;
– имя программы;  – формальный параметр;
– формальный параметр;  – фактический параметр, подставляемый вместо формального. Оператор осуществляет пропуск четных чисел.
– фактический параметр, подставляемый вместо формального. Оператор осуществляет пропуск четных чисел.
2.Суммирование элементов последовательности до первого отрицательного элемента.
Пояснение к программе: Здесь,  – имя программы. Оператор
– имя программы. Оператор  осуществляет досрочный выход из цикла при встрече с первым
осуществляет досрочный выход из цикла при встрече с первым
отрицательным числом.
3. Вывести первый отрицательный элемент последовательности.
87

Пояснение к программе: Здесь,  – имя программы. Оператор return прекращает выполнение программы и возвращает значение первого отрицательного элемента последовательности.
– имя программы. Оператор return прекращает выполнение программы и возвращает значение первого отрицательного элемента последовательности.
Упражнение 1
Составить блок – схему и программу нахождения суммы ряда y = x3 −x 1 ,
где, a x b , x меняется с шагомh =1,
а) используя цикл ; б) используя обычный оператор цикла ;
в) используя модифицированный оператор цикла .
а) Решение с помощью оператора while
Порядок выполнения:
1.Составьте блок – схему.
2.Запишите формулировку задания в Текстовое поле.
3.Запишите 

 и затем на вкладке Программирование выберите оператор создания программы
и затем на вкладке Программирование выберите оператор создания программы 
4.Наберите необходимые операторы, используя при этом оператор
локального присваивания вместо обычного . |
|
|
5. Проверьте работу программы при |
и |
. |
Блок-схема: Введем обозначения: f 1 – |
числитель, f 2 |
– знаменатель. |
Начало |
|
|
a,b
S:=0, x:=a
-x
S
Конец
88

Вид документа Mathcad Prime:
Пояснение к программе: Здесь, |
|
– |
имя программы; |
– |
|
формальные |
параметры; |
и |
– |
фактические параметры, |
|
подставляемые вместо формальных; |
– искомая сумма. До входа в цикл |
||||
переменным |
и присваиваются начальные значения. В соответствии |
||||
с условием задачи, в теле цикла |
|
, происходит накапливание суммы |
|||
и изменение значения переменной |
на |
. Если не менять значение |
, |
||
то произойдет так называемое «зацикливание», т.к. условие окончания цикла 
 никогда не выполнится и соответственно циклический процесс не остановится (Cikl1_1).
никогда не выполнится и соответственно циклический процесс не остановится (Cikl1_1).
Примечание: Обычно, при нахождении суммы , его значение вначале считают равным . Добавление числа  не изменяет значение суммы, однако упрощает организацию цикла. При нахождении произведения
не изменяет значение суммы, однако упрощает организацию цикла. При нахождении произведения  его значение вначале считают равным . Умножение числа на
его значение вначале считают равным . Умножение числа на  не изменяет значение произведения, однако упрощает организацию цикла.
не изменяет значение произведения, однако упрощает организацию цикла.
б) Решение с помощью обычного оператора цикла for
Порядок выполнения:
1.Составьте блок – схему.
2.Запишите формулировку задания в Текстовое поле.
3.Запишите 

 и затем на вкладке Программирование выберите оператор создания программы
и затем на вкладке Программирование выберите оператор создания программы 
89

4. Наберите необходимые операторы, используя при этом оператор локального присваивания  вместо обычного .
вместо обычного .
5. Проверьте работу программы при 
 и
и  .
.
Блок-схема:
Начало
a,b
S:=0
- x,a
S:=S
S
Конец
Вид документа Mathcad Prime:
Пояснение к программе: Здесь, |
|
– |
имя программы; |
– |
|
формальные |
параметры; |
и |
– |
фактические параметры, |
|
подставляемые вместо формальных; |
– искомая сумма. До входа в цикл |
||||
переменной |
присваивается начальное значение . В соответствии с |
||||
условием задачи, в теле цикла |
, происходит накапливание суммы . |
||||
Заголовок оператора цикла – |
|
|
обеспечивает присваивание |
||
переменной |
, начального значения |
и его автоматическое увеличение |
|||
на , после каждого выполнения тела цикла (Cikl1_2).
90
