Метод._MathCAD_Prime / Метод._MathCAD_Prime

Добавил:

aabuchba Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Абхазский государственный университет

Предмет:

Информатика

Файл:

+ x , если x 3

− 8, если х 3

.pdf

Скачиваний:

206

Добавлен:

04.08.2021

Размер:

8.48 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 138 9 10 11 12 13 > Следующая >>>

Пример:

Здесь оператор используется для того, чтобы избежать деления на нуль.

В программах, для составления составных (сложных) условий, могут быть использованы логические операторы, которые выбираются на вкладке Математика/ Операторы/Сравнение.

Логические операторы Mathcad Prime:

Оператор		Описание

	(логическое “И”): возвращает , если		и	истинны.
	В противном случае возвращает .

	(логическое	“ИЛИ”): возвращает ,	если	или
	истинны или оба. В противном случае возвращает .

(исключающее “ИЛИ”): возвращает , если истинно либо или , но не оба одновременно. В противном случае возвращает .

(логическое “НЕ”): возвращает , если ложно. В противном случае возвращает .

– вещественные или комплексные скаляры, – истина, – ложь.

Упражнение 1

Составить блок – схему и программу для вычисления значения функций:

Порядок выполнения:

1.Составьте блок – схему.

2.Запишите формулировку задания в Текстовое поле.

3.Запишите и затем на вкладке Программирование выберите оператор создания программы

4.Наберите необходимые операторы, используя при этом оператор

локального присваивания вместо обычного .

5.Проверьте работу программы при и

1.Блок – схема:

Начало

-	x 3	+
	x 3

Конец

Вид документа Mathcad Prime:

Пояснение к программе: Здесь, – имя программы; – формальный параметр; – имя результата; и – фактические параметры, подставляемые вместо формального. В данном случае проверяется только первое условие (можно любое), т.к. эти условия взаимно – дополняемые (Vetv1).

Упражнение 2

Составить блок – схему и программу для вычисления значения функций:

4х − 5, если x 6 y = 4 − 5x, если х 3 .

Порядок выполнения:

1.Составьте блок – схему.

2.Запишите формулировку задания в Текстовое поле.

3.	Запишите			и затем на вкладке Программирование выберите
	оператор создания программы
4.	Наберите необходимые операторы, используя при этом оператор
	локального присваивания вместо обычного .
5.	Проверьте работу программы при					и	.
Блок – схема:
				Начало
				x
		-		x >6	+
				x >6
	-	x < 3	+		y:=4*x-5
		x < 3			y:=4*x-5

y:="Н.Р." y:=4-5*

Конец

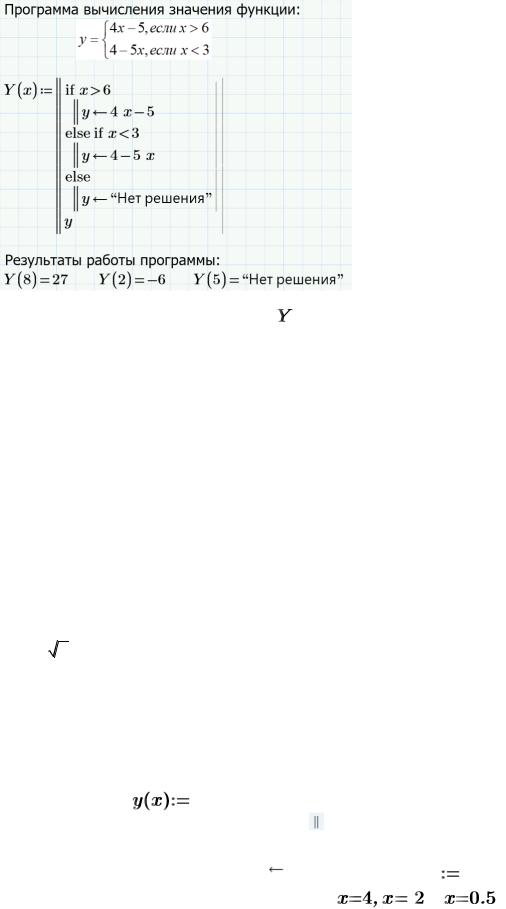
Вид документа Mathcad Prime:

Пояснение к программе: Здесь, – имя программы; – формальный параметр; – имя результата; и – фактические параметры, подставляемые вместо формального. В данном случае проверяются оба условия, т.к. эти условия не взаимно – дополняемые. Для случая, когда оба условия не верны, вывод результата осуществлен в виде текстового сообщения “Нет решения” (Vetv2).

Примечание: Текстовое сообщение необходимо заключать в кавычки типа “ ”.

Упражнение 3

Составить блок – схему и программу для вычисления значения функций:

x2 −1, если 0 x 1

y = 1 / x , если x 1

x3 +1, если x 0

Порядок выполнения:

1.Составьте блок – схему.

2.Запишите формулировку задания в Текстовое поле.

3.	Запишите	и затем на вкладке Программирование выберите
	оператор создания программы
4.	Наберите необходимые операторы, используя при этом оператор
	локального присваивания вместо обычного .
5.	Проверьте работу программы при		- и	.
		74

Блок – схема:

	Начало
	x
-	x >1	+
	x >1

-	x	0	+

Конец

Вид документа Mathcad Prime:

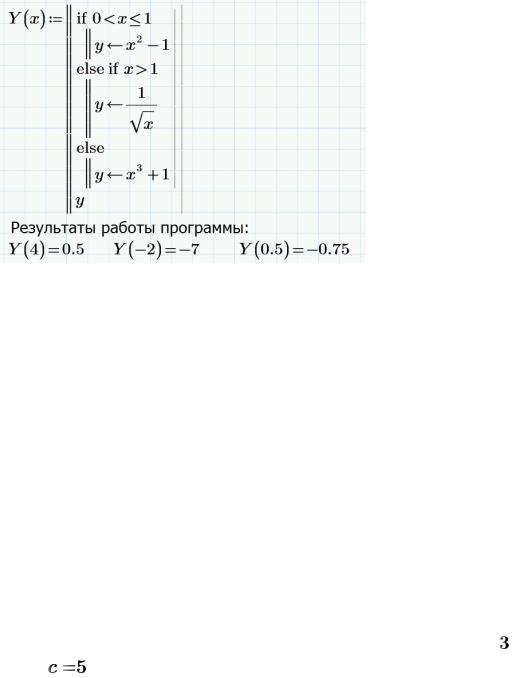
второе и третье условия (можно любые), т.к. эти условия взаимно – дополняемые (Vetv3).

Примечание: Т.к. Mathcad Prime позволяет записывать двойные неравенства в естественном виде, то решение предыдущей задачи мог бы быть и таким:

Упражнение 4

Составить блок – схему и программу нахождения действительных корней квадратного уравнения ax2 + bx + c = 0, a 0 .

Порядок выполнения:

1.Составьте блок – схему.

2.Запишите формулировку задания в Текстовое поле.

3.Запишите и затем на вкладке Программирование выберите оператор создания программы

4.Наберите необходимые операторы, используя при этом оператор локального присваивания вместо обычного

Проверьте работу программы при и

Блок – схема:

Начало

a,b,c

D:=b*b-4*a*c

-D 0 +

'Н.Р.'

x1,x2

Конец

Вид документа Mathcad Prime:

Пояснение к программе: Здесь,	–	имя программы;	и –
формальные параметры; (	) и (	) – тройки фактических
	77

параметров, подставляемые вместо формальных. В данном случае проверяется условие , необходимости в проверке условия нет, т.к. эти условия взаимно – дополняемые. При найденные корни выводятся в виде вектора – столбца (можно и виде вектора – строки), а при результат выводится в виде текстового сообщения “Нет решений“ (Vetv4).

Примечание: Некоторые, несложные задачи на реализацию разветвляющегося вычислительного процесса можно решать и без использования вкладки Программирование. Для этого в Mathcad Prime имеется оператор условного ветвления . Оператор реализует логическую структуру «ЕСЛИ-ТО-ИНАЧЕ».

Формат: , что соответствует конструкции (если то иначе ), Где, – логическое выражение(условие),

и – некоторые выражения, произвольные числа, массивы или строки либо функции, при вычислении которых получается результат одного из этих типов.

Принцип работы: где, – истина, –ложь.

- управляющий оператор PTC Mathcad, который, в отличие от функций, не работает с операторами, изменяющими функции, например, с оператором умножения векторов.

Важно! Оператор необходимо набирать с помощью клавиатуры.

х2 +1, при x 3

Пример: Найти значение функции: y =

х − 8, при х 3

Решение:

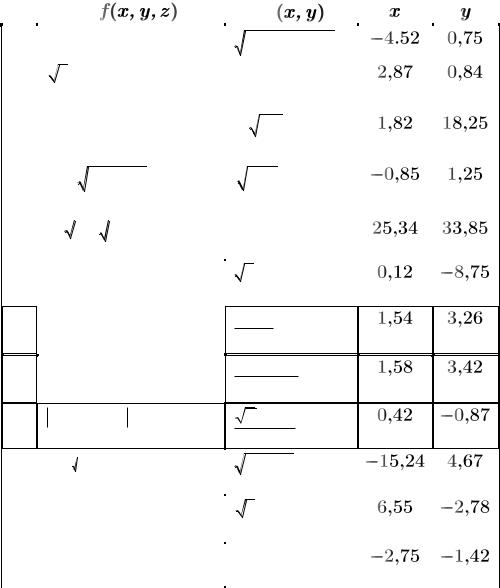
Индивидуальные задания

1. Составить блок – схему и программу для вычисления значения функций f (x, y, z) , где, z = w(x, y) . Значения x и y заданы в Табл 1.

2. Составить блок – схему и программу вычисления значения функции:

f 1( x), если x 0

Y= f 2( x), если 0 x 1

f 3( x), если x 1

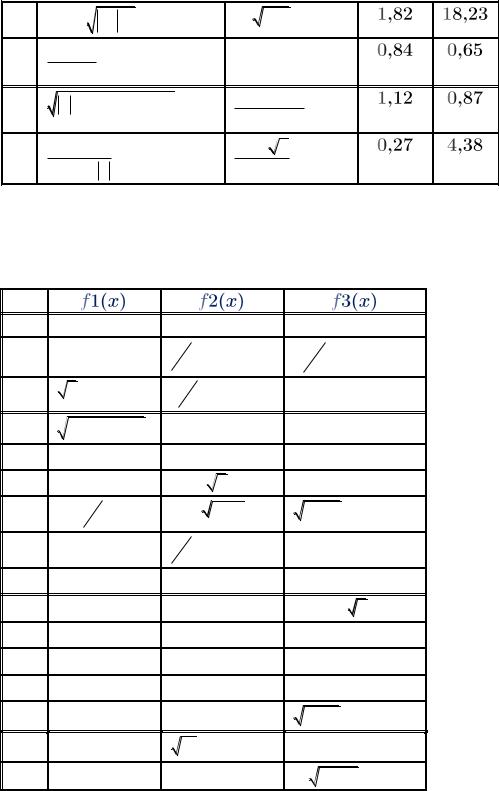
Функции f 1(x), f 2(x), f 3(x) заданы в Табл. 2.

3.Составить программу вычисления значения функции. Функции заданы в Табл. 3.

Таблица 1

№

e−2 x (tg(z) + 2 y)

sin2 x +

+ y

2 xy

x + sin(2 y)

x + cos y

x + e

y + z / ( y − x)

15 y

cos x + ( y − x)2

y + ctg(x)

yx + 3

20x

x2 + y3

sin(x / y)

ln(

x − y + 2)z3

2x2

xarctg(z)

y +

x sin y

y + x2


	z3
x + y3		/ x + z2
z2		+ sin( y / 5)
y + x3		+ sin( y / 5)

cos x + sin y − 2tg2 (z)

x + ey

cos2 y + 3

x sin2 y

x + ey

3x + 2 y

ln y

(z2 −

)

sin( x)

xarctg(2 y)

+ sin( y / 5)

y + x3

ey+x

cos2 z +

x + y

x + ey

13	x y / x + 3 y z ex	ln( ex− y	+ y2 )
14	ez−1	cos2 y + sin3 x2
	2 y + x3 + sin y
15	y e−( y+x) − cos(z3 )	x + 6 y
		sin x + ln y
16	4 y2e3x	x + y x
	8z3 + ln x	x +10

Таблица 2
№
1	tg(2x)	sin(3x)		cos(x − 2)
2	4x + 2	5	( x + 0, 4)	0,5
				2sin(4x)
3	3 x −1	x4		sin3 (2x)
			7
4	3 sin2 ( x) + x4	ctg(x +0,4)		ln(2x +0,5)
5	x3 − ln(\| x \|)	ln3 ( x + 4)		x4 − x2−x
6	sin( x2 )	e− x + 4 x		ln( x3 + x2 )
7	3x −1		2		2
		ln (\| x + 5 \|)		1+ x

	x5
8	x cos(x)	1	tg(2x) +1	x2e−x

9	x1.2 sin(3x)	cos( x2 )		sin(x2 ) + x0.25
10 x2x+1		sin( x2 )		ln2 ( x) +		x
11 sin2 (x3 )		sin(2x)		2 sin(x − e−x )
12 2xe−x		cos(2x)		xx − cos(x)
13	ln(2x +5)	sin(ex )		1/ tg(x)
14	sin(2x +1)	(x +1)2 cos(x3 )		x3 −1 + sin(x2 )
15	cos(x)	x3 sin(x)		x2 + sin(x2 )
16	x(sin(x) + 2)	ln(4x +1)2		ln 5 x + x2

<<< < Предыдущая 1 2 3 4 5 6 78 / 138 9 10 11 12 13 > Следующая >>>