Метод._MathCAD_Prime / Метод._MathCAD_Prime

Добавил:

aabuchba Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Абхазский государственный университет

Предмет:

Информатика

Файл:

Найти аналитическое решение неопределенного интеграла

.pdf

Скачиваний:

198

Добавлен:

04.08.2021

Размер:

8.48 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Упражнение 2

Найти аналитические выражения производных порядка функции из упражнения 1.

Порядок выполнения:

n = 1, 2, 3 для

1.Запишите заданную функцию:

2.На вкладке Математика/Операторы выберите , появится знак производной, которую заполните соответствующим образом.

3.На вкладке Математика/Символьные вычисления выберите оператор аналитических преобразовании , затем нажмите или щелкните мышью любое другое место.

4.Для упрощения полученных выражений используйте ключевое слово (Упрощение алгебраических выражений) из вкладки Математика/Символьные вычисления, затем нажмите

или щелкните мышью любое другое место.

Вид документа Mathcad Prime:

2. Вычисление интегралов

Упражнение 1

4
	x − 3 2x
Найти определённый интеграл			dx .

1		x

Порядок выполнения:

1.Запишите подынтегральную функцию:

2.На вкладке Математика/Операторы выберите , появится знак интеграла, которую заполните соответствующим образом:

где, и – вставляют нижний и верхний пределы интегрирования; – имя функции; – имя переменной. Данный оператор используется и для вычисления неопределенных интегралов, при этом поля и не заполняются.

3. Для получения результата наберите знак равенства =.

Вид документа Mathcad Prime:

Упражнение 2

Порядок выполнения:

1.Запишите заданную подынтегральную функцию:

2.На вкладке Математика/Операторы выберите , появится знак интеграла, которую заполните соответствующим образом.

4.Для упрощения полученного выражения используйте ключевое

слово (Разложение на множители) из вкладки Математика/Символьные вычисления, затем нажмите или щелкните мышью любое другое место.

Вид документа Mathcad Prime:

Индивидуальные задания

1.Вычислите первую и вторую производную функции.

2.Вычислите значение определенного интеграла.

3.Вычислите значение неопределенного интеграла.

4.Найдите значение производной функции f (x) в точке x0 .

Таблица заданий:

№

Задание 1

Задание 2

Задание 3

Задание 4

1,4

x0 = 1,

+ 5dx

y = ln x −

+ 5

1 − x

2x +

+ 0,5

0,6

f ( x) = x3 + 3

y = (x − 0,5)

−

ln x

0,8

sin(2x + 0,5)dx

x0 = 3,

− x dx

2 + cos( x

+1)

x 3

0,2

x +

f ( x) = 3 − x

ln x

sin(0, 3x + 0,8)dx

x0 = −1,

y = (2x −8)

− cos x dx

f ( x) = ln x + x3

0, 9 + 2 sin(0, 4x + 0, 3)

x +1

0,2

1,8

x3 −1

x0 = 3,

y = sin

−

0,8x2 +1dx

0,8

− cos x dx

f ( x) = x

ln x

x + 1,5x2 + 2

x2 +1

1,4

ln x

x0 = 3,

0,1x2 + 2dx

−

y =

f ( x) = (1 − ln x)x

1 − 3x

+ 2

0,8

2 + x2

x0 = 3,

y = ln

2x2 + 0, 7dx

x +1

f ( x) = x

− 3ln x

1,5 +

0,8x +1

1,2

x2 −1

2,1

2x2 +1

x0 = 3,

2x2

+1, 6dx

y =

− ln

ln x − 2

2x − 2

2x +

0,5x

+ 3

f ( x) =

1,2

ln x

1 − x2

1,4

cos x

x0 = 2,

x2 + 0,5dx

y =

−

x −

x +

2x +

+ 2,5

f ( x) =

ln x +1

0,6

ln x

1,3

sin(0, 5x + 0, 4)dx

xdx

x0 =1,

x + 3 − 2x

y =

1, 2 + cos(x

+ 0, 4)

2x2 −3x − 2

f (x) = ln 3x

0,5

ln x

2,6

0, 4x +1, 7dx

x −1

x0 =1,

y =

+ 3 −

1,5x +

+1,3

x2 + 4 dx

f (x) = ln10x

1,2

1,5

sin (0, 3x +1, 2)dx

x0 =1,

y =

−

− x

0,3

1, 3 + cos

(0, 5x +1)

− x dx

f (x) = ln x e

x +

x3 −1

0,8

cos

(

x2 +1 dx

x4 +1

x0 =1,

y = ln

x −

)

− x dx

0,2 2 + sin (2x + 0, 5)

f (x) = x

0, 6x +1, 7dx

x0 =1,

y = ln

− x

1,2 2,1x +

f (x) = ln(2x2 −3)

1 − x

0, 7x2 +1

x +

(1 + x

)

1,3

cos

(

x2 0, 2

)

(

x +1 + x)dx

x0 = 1

y =

3x3

− 2

0,5 1,3 + sin (2x + 0, 4)

5 − x

f ( x) = ln

5 + x

1,2

sin

1, 5x + 0, 3

)

x =1,

y =

(1 − x

)

(

x + 0,5

0,4 2, 3 + cos (0, 4x2 +1)

− x dx

f (x) = lg(2x +1)

x −1

2,8

1, 2x + 0, 7dx

x0 =1,

y =

− 2x

x − x

1, 4x +

1,3x

+ 0,5

x + 2

− x

f (x) = ln

2x −1

1,2

2x −1

3. Программирование в системе Mathcad Prime

Используя совместно функции Mathcad и операторы программирования, можно составлять довольно сложные программы. Например, можно составить программу для выполнения следующих действий.

•Вызов встроенных констант и функций.

•Обращение к определенным ранее переменным и функциям.

•Использование логических операторов совместно с условными операторами.

•Использование операторов для работы с массивами, например, оператор элемента в матрице, совместно с переменными итерации.

•Определение нескольких результатов при обработке матрицы или вложенной матрицы.

ВMathcad создание программ осуществляется с помощью оператора "программа – ". Этот оператор является многошаговым контейнером для управляющих операторов Mathcad, которые осуществляют выполнение следующих функций:

•назначение математических выражений локальным переменным или функциям;

•проверка условий ветвления;

•выполнение расчетов в цикле;

•добавление точек останова;

•отслеживание ошибок.

Для составления программ (подпрограмм – функций) в Mathcad Prime имеется специальная вкладка Программирование:

Алгоритмические конструкции (операторы) в среде Mathcad вводятся не традиционным набором через клавиатуру ключевых слов и т. д., а нажатием одной из соответствующих кнопок панели инструментов Математика/Программирование или с использованием сочетания клавиш, предусмотренных для этих целей (см. Табл. внизу)

Необходимо отметить, что использование в программах обычного оператора присваивания ( ) вызовет ошибку. Вместо него необходимо использовать оператор локального присваивания . Также в программах, в определениях условия (логическое выражение) нельзя использовать обычный знак равенства =, вместо него необходимо использовать оператор сравнения (жирный знак равенства ).

Примечание: При создании программ, оператором локального присваивания приходится пользоваться часто, при этом полезно, для ввода этого оператора пользоваться клавишей { .

Общий вид программы:

Где, Name – имя программы, Param – формальные параметры, S – оператор(ы), Res – результат.

Примечание: Формальные параметры могут отсутствовать.

Mathcad - программа возвращает результат на последнем шаге. Причем, в качестве результата может возвращаться единственный «объект». «Объект» может представлять собой: любое число, в т.ч. комплексное; текстовое сообщение, заключенное в кавычки (“”); вектор или матрица (допускается вложенность), для случая, когда результат работы не может быть представлен единственным числом, например, корни квадратного уравнения. Аналогами одномерного массива являются вектор – строка и вектор – столбец, а двумерного массива – матрица. Для функций, получающих векторный аргумент, обычно требуется вектор-столбец.

Лабораторная работа №6. Программирование линейного и разветвляющегося вычислительных процессов

Линейным называется вычислительный процесс (алгоритм), в котором операторы (команды) выполняются последовательно, один за другим. Понятие алгоритма и правила записи алгоритма в виде блок-схемы даны в Приложении.

Упражнение

Составить блок – схему и программу для вычисления значения функций:

				3y
		+ z3 , где,			и с ее помощью вычислить конкретное
f = ex−1 −	y		z =

				+ ex− y
			3
			3

значение этой функции при x = 3, 91 ; y = −0,51.

Порядок выполнения:

1.Составьте блок – схему.

2.Запишите формулировку задания в Текстовое поле.

3.Запишите и затем на вкладке Программирование выберите оператор создания программы

4.Наберите необходимые операторы, используя при этом оператор

локального присваивания вместо обычного .

5. Проверьте работу программы при	и
Блок-схема:
Начало
x, y

Конец

Вид документа Mathcad Prime:

Пояснение к программе: Здесь,	– имя программы; и – формальные
параметры; – имя результата;	и	– фактические значения

соответствующих формальных параметров (Lin1).

Примечание: В последней строке программы записывают имя результата.

Разветвления в программе возникают при необходимости выбора одного из нескольких возможных путей в решении задачи.

Для организации разветвлений в программах на Mathcad Prime


используются операторы ,		,	и	. Первым, оператором
должен быть	, который		является	«заголовком» начала
разветвляющегося процесса.

Операторы условного перехода выбираются на вкладке

Математика/Программирование и позволяют изменить порядок выполнения операторов в программе в зависимости от определенных условий. Оператор может использоваться в двух формах:

а) Полная форма ветвления:

принцип работы –

Где, – логическое выражение (условие), и – операторы языка программирования Mathcad Prime, – истина, –ложь.

Если условие , заданное в операторе , истинно, то выполняется оператор (простой или составной), стоящий во второй строке. В противном случае выполняется оператор , стоящий после . После выполнения одной из ветвей, работа программы продолжается с оператора, следующего за .

б) Сокращенная форма ветвления:

принцип работы –

Где, – логическое выражение (условие), – оператор (ы) языка программирования Mathcad Prime, – истина.

Если условие , заданное в операторе истинно, то выполняется оператор (простой или составной), стоящий во второй строке. В противном случае работа программы продолжается с оператора, следующего за .

Для организации более сложных разветвляющихся вычислительных процессов используют (иначе если) из вкладки

Программирование. Принцип работы:

где, и В – логические выражения (условия), и – операторы языка программирования Mathcad Prime, – истина, –ложь.

Понятие взаимно – дополняемых условии:

1.Два условия называются взаимно – дополняемыми, если ложность одного из них влечет за собой истинность другого.

2.Три условия называются взаимно – дополняемыми, если ложность любых, двух из них, влечет за собой истинность третьего.

Примеры: x 5 и x<5 , x = 0 и x 0 – взаимно – дополняемые условия;

x 5 и x<4 ,	x = 0 и x 0 – не взаимно – дополняемые условия;
x 5, x<3 и	3 x 5 , x 0, x<0 и x = 0 – взаимно – дополняемые условия;
x 5, x<3 и	3 x 4 , x 0, x<0 и x 0 – не взаимно – дополняемые условия.

Примечание:

1.В случае двух взаимно – дополняемых условии, проверяется только одно (любое), а в случае трех взаимно – дополняемых условии, проверяются только любые два из них.

2.В случае двух не взаимно – дополняемых условии, проверяются оба, а в случае трех не взаимно – дополняемых условии, проверяются все три.

Оператор ошибки Try/On

принцип работы –

Где, — любые допустимые выражения или последовательности выражений. Допустимы, например, локальное назначение, вызов функции или последовательность шагов программы.

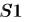Выполняется . Если при выполнении возникает ошибка, то выполняется и возвращается результат. В противном случае возвращается результат выполнения . Оператор отличается от всех других условных операторов. Он меняет направление выполнения программы только в случае возникновения ошибки при расчете.

Местозаполнитель должен содержать выражение, которое всегда выполняется без ошибок. Оператор можно использовать для вывода переменных при отладке программы, для выполнения другого расчета или выхода из программы с выдачей сообщения об ошибке.

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>