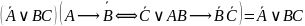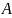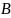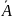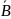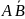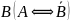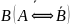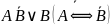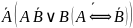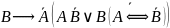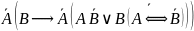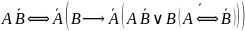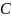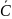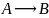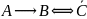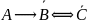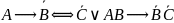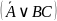П.Р.№1 Шерстюк

Шерстюк П.В., З-66, вариант 19

1. Упростите выражения:

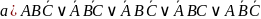
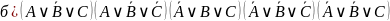
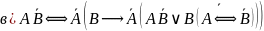
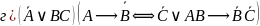
Сначала преобразуем :

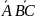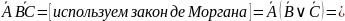
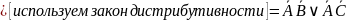
Получаем дизъюнктивную нормальную форму:

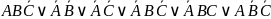
Далее, преобразуем 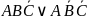и :

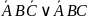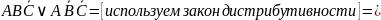
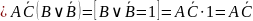
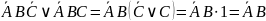
Получаем:

Далее,

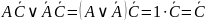
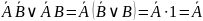
В итоге получаем:

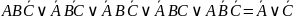
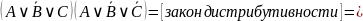
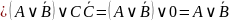
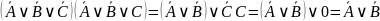
Получаем пока:

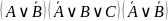
Далее:

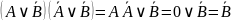
Получаем:

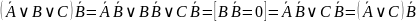
В итоге получаем:

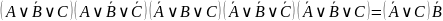
Импликацию и эквивалентность заменим по законам 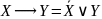и .

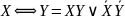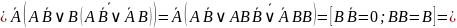
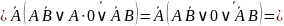
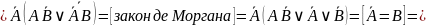
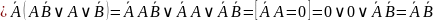
Тогда:

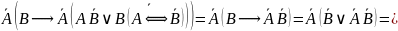
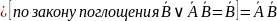
Получаем:

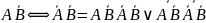
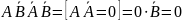
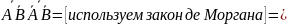
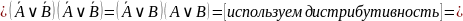
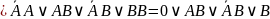
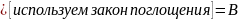
В итоге получаем:

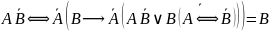
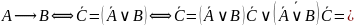
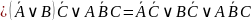
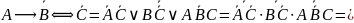
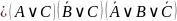
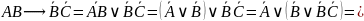
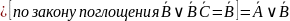
Тогда:

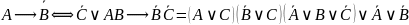
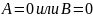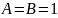Рассмотрим правую часть. Она равна 1 при . Рассмотрим случай . Тогда:

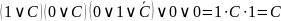
Тогда:

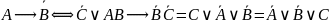
Наконец,

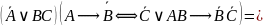
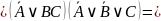
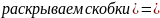
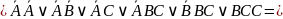
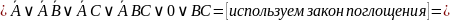
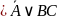
2. С помощью таблиц истинности докажите правильность упрощения (для примеров в и г).

Строим последовательно таблицу истинности. Учитываем, что отрицание меняет истинность, дизъюнкция ложна только в случае, когда ложны все логические слагаемые, конъюнкция истинна только в случае, когда истинны все логические сомножители, импликация ложна только в случае, когда из истины следует ложь, эквиваленция истинна при совпадении логического значения операндов.

0	0	1	1	0	0	0	1	1
0	1	1	0	0	1	1	0	0
1	0	0	1	1	1	0	1	1
1	1	0	0	0	0	0	1	1

(продолжение таблицы истинности)

1	1	1	0
0	0	0	1
0	1	0	0
0	0	0	1

Видим по таблице истинности, что заданное логическое выражение совпадает по истинности с переменной , т.е. убеждаемся, что

Строим последовательно таблицу истинности. Учитываем, что отрицание меняет истинность, дизъюнкция ложна только в случае, когда ложны все логические слагаемые, конъюнкция истинна только в случае, когда истинны все логические сомножители, импликация ложна только в случае, когда из истины следует ложь, эквиваленция истинна при совпадении логического значения операндов.

0	0	0	1	1	1	1	1	1	0
0	0	1	1	1	0	1	1	0	1
0	1	0	1	0	1	1	1	1	0
0	1	1	1	0	0	1	1	0	1
1	0	0	0	1	1	0	0	0	1
1	0	1	0	1	0	0	0	1	0
1	1	0	0	0	1	0	1	1	0
1	1	1	0	0	0	1	1	0	1

(продолжение таблицы истинности)

0	0	0	1	1	1
0	0	1	1	1	1
0	1	0	1	1	1
0	1	1	1	1	1
1	0	0	1	1	0
1	0	1	1	1	0
1	1	0	0	0	0
1	1	1	0	1	1

Видим по таблице истинности, что заданное логическое выражение совпадает по истинности с выражением , т.е. убеждаемся, что