
Лекция№9 электромагнитные колебания22.03.21
.docx
Затухающие колебания.
В рассмотренном примере электромагнитных гармонических колебаний не учитывались потери энергии, связанные с выделением теплоты на активном сопротивлении, всегда присутствующем в реальной электрической цепи. Поэтому рассмотренные колебания можно назвать свободными идеальными незатухающими колебаниями. При потере системой энергии в процессе колебаний амплитуда колебаний уменьшается.
Затухающими называются колебания, амплитуда которых уменьшается с течением времени.
Рассмотрим свободные затухающие колебания. В реальном колебательном контуре кроме катушки индуктивности L, конденсатора емкости С и ключа К имеется активное сопротивление R (рис. 1).
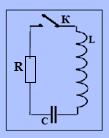
Рис. 1.
Запишем для контура уравнение по второму правилу Кирхгофа с учетом активного сопротивления цепи R:
Uc
+ IR=
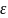 S
, то есть напряжение на обкладках
конденсатора плюс напряжение на
сопротивлении R
равно ЭДС самоиндукции.
S
, то есть напряжение на обкладках
конденсатора плюс напряжение на
сопротивлении R
равно ЭДС самоиндукции.
Но
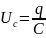 ,
,
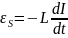 . Отсюда:
. Отсюда:
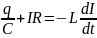
По
определению, сила тока I=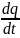 . Тогда предыдущее уравнение преобразуется
к виду:
. Тогда предыдущее уравнение преобразуется
к виду:
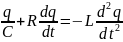 или,
или,
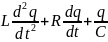 = 0 , или
= 0 , или
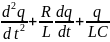 = 0, или
= 0, или
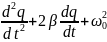 q
=
0,
где
q
=
0,
где
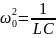 - собственная частота контура, β
=
- собственная частота контура, β
=
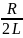 - коэффициент затухания. Чем больше R
и меньше L,
тем больше коэффициент затухания.
- коэффициент затухания. Чем больше R
и меньше L,
тем больше коэффициент затухания.
Это уравнение есть однородное дифференциальное уравнение второго порядка для затухающих колебаний.
Решениями этого уравнения являются функции:
 .
(1)
.
(1)
Здесь
- частота колебаний заряда на
конденсаторе, напряжения на конденсаторе,
силы тока в цепи,
- коэффициент затухания, который
определяет скорость убывания амплитуды
колебаний. Циклическая частота колебаний
определяется по формуле:
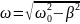 , qm
–
начальное значение амплитуды, φ –
начальная фаза колебаний. Чем меньше
β, тем меньше затухание колебаний.
, qm
–
начальное значение амплитуды, φ –
начальная фаза колебаний. Чем меньше
β, тем меньше затухание колебаний.

.
Пусть
заряд на конденсаторе изменяется по
закону косинуса:
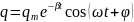 .
График этой функции представлен на
рис. 2. Верхняя пунктирная линия
представляет собой закон изменения
амплитуды колебаний q(t)
=
.
График этой функции представлен на
рис. 2. Верхняя пунктирная линия
представляет собой закон изменения
амплитуды колебаний q(t)
=
 . Очевидно, что амплитуда со временем
убывает по экспоненте.
. Очевидно, что амплитуда со временем
убывает по экспоненте.

Рис. 2.
Найдем
выражение для силы тока в контуре:
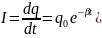 . (2)
. (2)
Пусть в начальный момент времени заряд равен qo , а сила тока равна нулю. Тогда из соотношений (1) и (2) получаем:
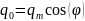 и
и
 .
.
Соответственно,
начальная
фаза оределяется
из соотношения:
tgφ
= -
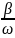 .
.
Согласно
тригонометрической формуле,
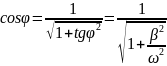
Тогда:
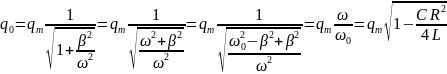 .
.
Отсюда,
начальная
амплитуда:
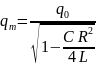 .
.
Таким образом, начальная фаза и начальная амплитуда колебаний в контуре зависят от его параметров: емкости, индуктивности и активного сопротивления.
Вернемся
к выражению (2) для силы тока и несколько
преобразуем его:
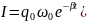 .
(3)
.
(3)
Представим
функцию сила тока следующим образом:
 . (4)
. (4)
С
учетом тригонометрических преобразований,
получаем:
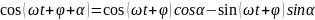 ,
,
или: (5)
Найдем изменение фазы α, сравнивая зависимости (3) и (5):
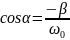 ,
и
,
и
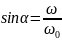 .
.
Отметим
для себя, что
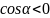 ,
а
,
а
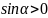 .
Следовательно, угол α лежит в пределах:
.
Следовательно, угол α лежит в пределах:
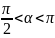 , то есть при наличии в контуре активного
сопротивления R
колебания тока опережают по фазе
колебания напряжения на конденсаторе
и колебания заряда более, чем на
, то есть при наличии в контуре активного
сопротивления R
колебания тока опережают по фазе
колебания напряжения на конденсаторе
и колебания заряда более, чем на
 . При отсутствии активного сопротивления
опережение составляет
.
. При отсутствии активного сопротивления
опережение составляет
.
Вернемся
к случаю собственных незатухающих
колебаний, рассмотренному на прошлой
лекции (R=0).
Амплитуда напряжения на обкладках
конденсатора
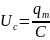 , а амплитуда силы тока
, а амплитуда силы тока
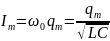 , тогда можно записать:
, тогда можно записать:
 ,
а величина
,
а величина
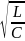 получила название волнового
сопротивления контура.
получила название волнового
сопротивления контура.
Период
Т затухающих колебаний в колебательном
контуре равен:
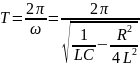 .
.
Когда
202,
или сопротивление R
очень мало, период колебаний практически
равен периоду собственных незатухающих
колебаний:
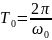 .
.
С
увеличением коэффициента затухания
,
когда растет сопротивления R,
период колебаний увеличивается, и
при
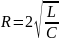 обращается в бесконечность. При 2
>02
(
обращается в бесконечность. При 2
>02
(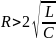 ), колебания не совершаются, а происходит
монотонная разрядка конденсатора. Такой
разряд называется апериодическим.
), колебания не совершаются, а происходит
монотонная разрядка конденсатора. Такой
разряд называется апериодическим.
Найдем время релаксации как время, за которое амплитуда колебаний уменьшается в e раз:
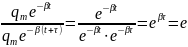
Отсюда,
= 1,
и
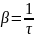 . Иначе: время релаксации – величина,
обратная коэффициенту затухания.
. Иначе: время релаксации – величина,
обратная коэффициенту затухания.
Для характеристики скорости затухания электромагнитных колебаний служат несколько параметров: декремент затухания D, логарифмический декремент и добротность Q.
Декремент затухания показывает, во сколько раз уменьшается амплитуда колебаний за время, равное периоду колебаний Т:
D
=
 ,
,
a(t) – амплитуда соответствующей величины – заряда на обкладках конденсатора, напряжения на конденсаторе, силы тока в цепи.
Натуральный логарифм от декремента затухания есть логарифмический декремент :
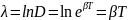 .
(6)
.
(6)
Так
как
, то
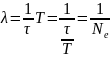 , где Ne
- число колебаний за время релаксации
, где Ne
- число колебаний за время релаксации
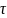 ,
или за время, за которое амплитуда
уменьшается в е раз.
,
или за время, за которое амплитуда
уменьшается в е раз.
Найλдем добротность Q колебательного контура. Этот параметр пропорционален отношению энергии системы в некоторый момент времени t к изменению энергии за период Т после t.
Q
= 2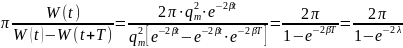 .
.
При
малых коэффициентах затухания
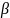 ,
и , соответственно,
,
и , соответственно,
 ,
можно получить:
,
можно получить:
Q
=
 .
(7)
.
(7)
То есть добротность пропорциональна числу колебаний, которые успевают совершиться за время релаксации.
Взяв
вместо логарифмического декремента
его значение βТ, получим
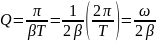 .
.
При
малых коэффициентах затухания
можно положить ω = ω0
=
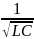 .
.
Тогда:
Q
=
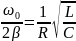 . (8)
. (8)
Вынужденные колебания. Резонанс.
Для получения незатухающих электромагнитных колебаний необходимо извне подводить энергию, компенсирующую потери при рассеивании джоулевой теплоты. В этом случае будут уже не свободные, а вынужденные электромагнитные колебания. Для осуществления таких колебаний необходимо включить в колебательный контур источник тока, обладающий периодически изменяющейся ЭДС ε = εm cos(Ωt+ψ ). Здесь Ω –греческая буква омега заглавная, частота внешней ЭДС.

Рис. 3.
Тогда, по аналогии с предыдущими случаями, дифференциальное уравнение электромагнитных колебаний с учетом внешней ЭДС запишется так:
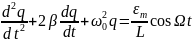 (9)
(9)
Решением неоднородного дифференциального уравнения второго порядка является сумма общего решения однородного уравнения и частного решения неоднородного:
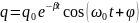 +
qm
cos(Ωt
+ψ
), ψ
– греческая буква пси, начальная фаза
вынужденных колебаний заряда.
+
qm
cos(Ωt
+ψ
), ψ
– греческая буква пси, начальная фаза
вынужденных колебаний заряда.
Поскольку первое слагаемое очень быстро стремится к нулю, то решением этого уравнения будет:
q = qm cos(Ωt - ψ) , (10)
причем Ω - частота вынужденных колебаний, совпадает с частотой колебаний внешней ЭДС, а ψ – начальная фаза вынужденных колебаний заряда.
Амплитуда установившихся вынужденных колебаний заряда qm является сложной функцией частоты внешней ЭДС Ω и коэффициента затухания :
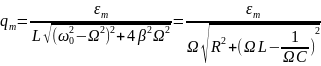 (11)
(11)
Зависимости
амплитуды колебаний заряда qm
от Ω и
представлены на рис.4 (123).
При Ω=0 все кривые сходятся в одной
точке оси ординат
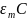 – это заряд на конденсаторе, возникающий
при подключении его к источнику
постоянного напряжения
– это заряд на конденсаторе, возникающий
при подключении его к источнику
постоянного напряжения
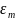 . При различных значениях
амплитудные кривые имеют максимумы,
которые соответствуют частотам:
Ω1
, Ω2
и Ω3
.
. При различных значениях
амплитудные кривые имеют максимумы,
которые соответствуют частотам:
Ω1
, Ω2
и Ω3
.
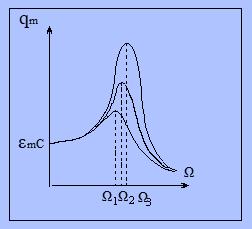
Рис. 4.
Начальная
фаза колебаний ψ определяется по формуле:
tg
ψ =
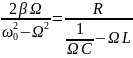 . (12)
. (12)
Зависимость
амплитуды вынужденных колебаний заряда
от частоты
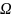 внешней ЭДС называется резонансной
характеристикой или резонансной кривой.
На графике рис.5 показаны резонансные
кривые для случаев: 1 – колебательная
система без сопротивления R,
при резонансе амплитуда вынужденных
колебаний неограниченно возрастает,
2, 3, 4 – реальные резонансные кривые для
колебательных систем с различными
сопротивления R
и, соответственно, разными коэффициентами
затухания (4
3
0
2).
Чем меньше сопротивление R,
тем больше и острее амплитуда вынужденных
колебаний при резонансе. При различных
значениях
резонансные характеристики имеют
максимумы, которые соответствуют
частотам: Ω1
, Ω2
, Ω3
, Ω4.
внешней ЭДС называется резонансной
характеристикой или резонансной кривой.
На графике рис.5 показаны резонансные
кривые для случаев: 1 – колебательная
система без сопротивления R,
при резонансе амплитуда вынужденных
колебаний неограниченно возрастает,
2, 3, 4 – реальные резонансные кривые для
колебательных систем с различными
сопротивления R
и, соответственно, разными коэффициентами
затухания (4
3
0
2).
Чем меньше сопротивление R,
тем больше и острее амплитуда вынужденных
колебаний при резонансе. При различных
значениях
резонансные характеристики имеют
максимумы, которые соответствуют
частотам: Ω1
, Ω2
, Ω3
, Ω4.

Рис. 5.
Частоты
Ω1,
Ω2,
... , которым соответствуют максимумы
амплитуды, называются резонансными
частотами Ωрез.
Чтобы определить их значения, необходимо
найти максимум для функции амплитуды
или, что то же самое, минимум знаменателя
функции А(Ω) -

 .
.
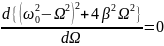 ,
,
2(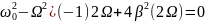 .
.
Значение
не равно 0, поэтому можно поделить
уравнение на
.
Получаем:
 .
.
Или,
значение частоты, при которой наблюдается
резонанс:
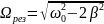 , или,
, или,
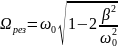 . (13)
. (13)
Найдем зависимость установившегося тока от времени:
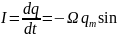 (
(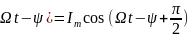
Амплитуда тока с учетом формулы амплитуды заряда имеет вид:

Резонанс
по току будет наблюдаться при частотах,
когда
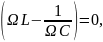 то есть при Ωрез=
ω0
.
то есть при Ωрез=
ω0
.
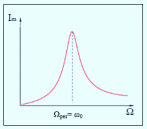
Рис. 6.
Резонансное
значение силы тока будет равно:
 .
.
Разделив заряд q на емкость С, получим напряжение на конденсаторе:
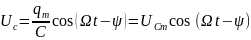 ,
,
где
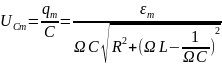
Отсюда
следует, что для резонанса напряжения
будет та же резонансная частота, что и
для заряда. Зависимости амплитуды
напряжения на обкладках конденсатора
от времени имеют характер, аналогичный
графикам на рис.5 для характеристик
заряда. При малом затухании, когда
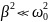 , резонансную частоту для напряжения
можно принять равной ω0
:
U
= ω0
=
.
, резонансную частоту для напряжения
можно принять равной ω0
:
U
= ω0
=
.
Тогда
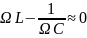 , и отношение амплитуды напряжения на
конденсаторе при резонансе к амплитуде
внешней ЭДС будет равно:
, и отношение амплитуды напряжения на
конденсаторе при резонансе к амплитуде
внешней ЭДС будет равно:
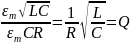 ,
,
где Q – добротность контура.
Последовательный колебательный контур широко применяется на практике в различных электро- и радиотехнических схемах и устройствах главным образом в качестве резонансной системы, то есть системы, усиливающей в Q раз гармонические колебания, поступающие на вход. Резонанс в контуре с последовательно соединенными индуктивностью и емкостью называют резонансом напряжений.
Переменный ток.
Закон Ома и правила Кирхгофа для постоянного тока будут справедливыми и для мнгновенных значений переменного тока и напряжения, если только их изменения не происходят слишком быстро. В пределах периода колебаний тока до 10-6 с токи можно считать квазистационарными. Рассмотрим частные случаи.
Переменный ток в цепи активного сопротивления.

Рис. 7.
Пусть
к сопротивлению R
(рис. 7 ), не обладающему емкостью и
индуктивностью, (такие сопротивления
называются активными), приложено
напряжение, изменяющееся по закону
косинуса: U=Umcoswt.
Тогда по закону Ома:
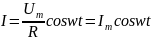 . Причем, для амплитудных значенийсоотношение
выглядит так:
. Причем, для амплитудных значенийсоотношение
выглядит так:
 .
.
Видно, что напряжение и ток изменяются синфазно, что можно показать с помощью диаграммы на рис. 8.

Рис. 8.
Переменный ток в цепи с индуктивностью.
Подадим переменное напряжение на концы индуктивности L, с бесконечно малым сопротивлением R и емкостью С. Схема цепи представлена на рис. 9.
Рис.9.
При
прохождении переменного тока через
индуктивность, возникнет ЭДС самоиндукции.
Тогда по закону Ома для неоднородного
участка цепи можно записать: Umcoswt
- L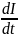 =0, или Umcoswt
= L
.
=0, или Umcoswt
= L
.
Поскольку все внешнее напряжение приложено к катушке, то UL = L -это падение напряжения на индуктивности. С помощью интегрирования получим выражение зависимости силы тока в цепи от времени:
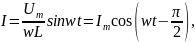 (14)
(14)
где
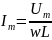 .
.
Роль сопротивления в данном случае играет величина XL = wL. Эту величину называют реактивным индуктивным сопротивлением, которое растет с увеличением частоты w.
Соответственно, падение напряжения на индуктивности: UL = wLImcoswt. (15)
Если сравнить выражение для тока (14) и выражение (15) стоновится видно, что падение напряжения на индуктивности опережает по фазе ток на . Диаграмма для тока и напряжения представлена на рис.10.
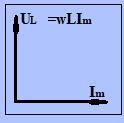
Рис. 10.
Переменный ток в цепи с электроемкостью.
Подадим переменное напряжение на обкладки конденсатора С, причем сопротивление и индуктивность подводящих проводов будем считать бесконечно малыми. Схема цепи представлена на рис. 11.
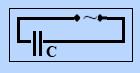
Рис. 11.
Напряжение
на конденсаторе будет равно внешнему
напряжению:
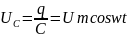 . (16)
. (16)
По определению, сила тока:
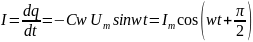 .
(17)
.
(17)
 ,
или
,
или
 .
Величина ХС
=
.
Величина ХС
=
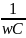 называется реактивным емкостным
сопротивлением.
называется реактивным емкостным
сопротивлением.
Напряжение
на конденсаторе
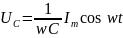 отстает по фазе от текущего через
емкость тока (17) на
(рис.12 ).
отстает по фазе от текущего через
емкость тока (17) на
(рис.12 ).
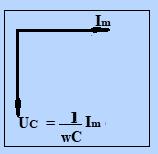
Рис. 12.
Цепь переменного тока, содержащая емкость, индуктивность и сопротивление.
Рассмотрим цепь, составленную из сопротивления R , емкости С и индуктивности L. Подадим на концы этой цепи напряжение
Umcoswt . В цепи возникнет переменный ток той же частоты w, амплитуда и фаза которого, как мы видели в случае колебательного контура, определяются параметрами цепи R, C, L. Этот ток вызовет на активном сопротивлении падение напряжения UR , фаза которого совпадает с фазой тока (рис.13).
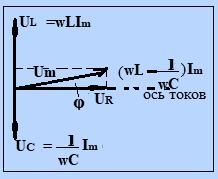
Рис. 13.
Падение напряжения на индуктивности и емкости отложены по вертикали, с учетом сказанного ранее. Падения напряжений UR, UL, UC в сумме должны быть равны приложенному напряжению U. Поэтому, сложив векторы UR, UL и UC мы получим вектор, показывающий U, а его длина равна Um. Этот вектор образует с осью токов угол φ, тангенс которого равен:
tg
φ =
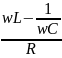 .
.
Этот угол φ показывает разность фаз между напряжением U и силой тока I. Из рис. 13 видно, что:
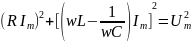 .
.
Откуда
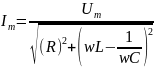
Итак, если напряжение на зажимах цепи Umcoswt , то в цепи течет ток I = Imcos(wt -φ) .
Величина
Z=
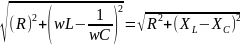 называется полным сопротивлением
цепи.
называется полным сопротивлением
цепи.
Величина
X=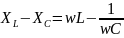 называется реактивным сопротивлением.
Таким образом,
называется реактивным сопротивлением.
Таким образом,
Z
=
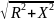 .
.
Ток
в цепи отстает от напряжения (φ>0)
или опережает его (φ
< 0)
в зависимости от соотношения между
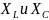 .
Если
.
Если
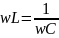 ,
изменения тока и напряжения происходят
синфазно. Сила тока в этом случае
максимальна. При этом падение напряжения
на активном сопротивлении равно внешнему
напряжению. Частота, при которой это
происходит, называется резонансной
частотой. При этой частоте напряжения
на емкости и на индуктивности равны по
амплитуде и противоположны по фазе
,
изменения тока и напряжения происходят
синфазно. Сила тока в этом случае
максимальна. При этом падение напряжения
на активном сопротивлении равно внешнему
напряжению. Частота, при которой это
происходит, называется резонансной
частотой. При этой частоте напряжения
на емкости и на индуктивности равны по
амплитуде и противоположны по фазе
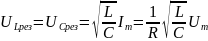 .
.
Мощность, выделяемая в цепи переменного тока.
Мнгновенное значение мощности, выделяемой в цепи, равно произведению мнгновенных значений напряжения и силы тока. С помощью тригонометрических преобразований можно получить выражение:
P(t)
=
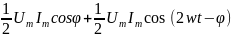 .
.
Среднее
по времени значение мощности Р=
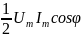 , так как среднее по времени от
, так как среднее по времени от
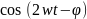 равно нулю. Из рис. 13 видно, что
равно нулю. Из рис. 13 видно, что
 .
.
Отсюда
P
=
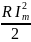 , такую же мощность развивает постоянный
ток I
=
, такую же мощность развивает постоянный
ток I
=
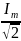 . Эта величина получила название
действующего
или
эффективного
значения силы тока.
Аналогично: U
=
. Эта величина получила название
действующего
или
эффективного
значения силы тока.
Аналогично: U
=
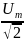 - действующее
значение напряжения.
С использованием действующих значений
средняя мощность выглядит так: P
= U
Icosφ
.
- действующее
значение напряжения.
С использованием действующих значений
средняя мощность выглядит так: P
= U
Icosφ
.
Приборы, работающие на переменном токе, встречаются во всех областях нашей жизни: при передаче энергии от источника потребителю, в генераторах переменного тока, трансформаторах. В технике часто стремятся сделать cosφ как можно больше для выделения необходимой мощности.
