Лекция№8 Уравнения Максвелла

Уравнения Максвелла.

Первое уравнение Максвелла. Рассмотрим случай электромагнитной индукции, когда ток индуцируется в неподвижном проводнике.

Согласно основному закону электромагнитной индукции, ЭДС индукции равна скорости изменения магнитного потока сквозь поверхность, ограниченную контуром:

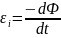, или, с учетом определения магнитного потока: 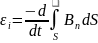(1)

Так как контур неподвижен, то изменение потока может быть обусловлено только изменением самого магнитного поля:

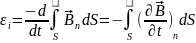, (2)

Здесь (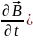 - частная производная от вектора магнитной индукции в некоторой неизменной точке поверхности.

С другой стороны, ЭДС по определению можно записать так: 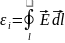(3)

Совместив соотношения (2) и (3), получим:

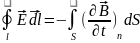
Это есть первое уравнение Максвелла, которое отражает закон электромагнитной индукции: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру равна взятой с обратным знаком, скорости изменения магнитного потока сквозь поверхность, ограниченную контуром.

Максвелл предположил, что изменяющееся со временем магнитное поле обусловливает появление в пространстве электрического поля напряженности Е, независимо от присутствия в этом пространстве проводящего контура. Наличие контура лишь позволяет обнаружить по возникновению в нем индукционного тока существование в соответствующих точках пространства электрического поля. Это электрическое поле, в отличие от электростатического, является вихревым, так как циркуляция напряженности этого поля по замкнутому контуру не равна нулю.

Явление возникновения в пространстве вихревого электрического поля под влиянием переменного магнитного поля было использовано для создания индукционного ускорителя электронов – бетатрона.

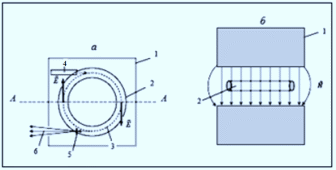
Рис. 1.

На рис. 1 представлена схема бетатрона. На рис. 1а - вид сверху, рис. б) - сечение по линии АА.

Рабочим циклом является первая (нарастающая) четверть периода магнитного поля. Конструктивно бетатрон представляет собой большой электромагнит (1), между полюсами которого расположена тороидальная вакуумная камера (2). Электромагнит создает в зазоре между полюсами переменное (меняющееся по закону синуса) магнтное поле напряженностью Н, которое в плоскости вакуумной среды создает вихревое электрическое поле напряженностью Е (ЭДС индукции). В вакуумную камеру с помощью инжектора (4 -электронная пушка) в начале каждого периода нарастания магнитного поля впрыскиваются электроны, которые увлекаются вихревым электрическим полем Е в процессе ускорения по круговой орбите (3).

Таким образом, электроны двигаются по круговой орбите постоянного радиуса в нарастающем во времени по синусоидальному закону магнитном поле. В момент, когда магнитное поле достигает максимума, процесс ускорения электронов прекращается и сменяется их замедлением, так как вихревое поле меняет направление, а ЭДС индукции – знак. Электроны, достигшие наибольшей скорости, смещаются с равновесной орбиты и либо выводятся из камеры, либо направляются на специальную мишень внутри камеры, называемую тормозной (5). Торможение электронов в этой мишени в кулоновском поле ядер и электронов приводит к возникновению электромагнитного тормозного излучения (6), максимальная энергия которого равна кинетической энергии электронов в конце ускорения. Тормозные фотоны летят в направлении движения первичных электронов в узком конусе.

Создание высокоэнергетичного электромагнитного γ – излучения торможением электронов в мишени – наиболее простой и эффективный способ создания пучка γ - квантов высокой энергии для экспериментов в ядерной физике. Бетатроны получили широкое применение в прикладных целях в диапазоне энергий 20-50 МэВ.

Второе уравнение Максвелла.

Повторим: Максвелл предположил, что изменяющееся со временем магнитное поле обусловливает появление в пространстве электрического поля напряженности Е, независимо от присутствия в этом пространстве проводящего контура.

Основная идея Максвелла заключается в том, что между электрическим и магнитными полями имеется и обратное соотношение, то есть что изменяющееся со временем электрическое поле должно приводить к появлению магнитного поля.

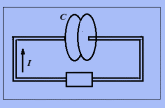
Рис. 2.

Рассмотрим магнитное поле вокруг провода, переносящего заряд от одной пластины конденсатора С к другой. Движение свободных носителей заряда имеет место во всей цепи, кроме зазора между обкладками конденсатора. Следовательно, линии тока проводимости терпят разрыв на границах обкладок конденсатора. В пространстве между обкладками имеется переменное электрическое поле, которое можно охарактеризовать вектором электрического смещения . 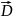Максвелл предположил, что линии тока проводимости непрерывно переходят на границе обкладок в линии тока, названного им током смещения.

Найдем выражение для плотности тока смещения. Для этого, выразим ток проводимости через его плотность тока.

I_пр = j∙S. С другой стороны, по определению для силы тока, .

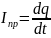Отсюда, j_пр = 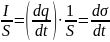, где σ – плотность заряда на обкладках конденсатора.

Исходя из теории Максвелла, линии тока смещения должны иметь такую же густоту, как и линии тока проводимости, то есть, плотность тока смещения должна быть равно плотности тока проводимости: j_пр = j_см .

В зазоре между двумя противоположно заряженными поверхностями вектор электрического смещения равен поверхностной плотности зарядов на этих поверхностях, или D = σ , отсюда: плотность тока смещения

j_смещ = .

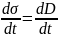Направление 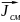совпадает с направлением производной : = .

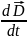Рассмотрим вновь понятие замкнутости цепей электрического тока. На рис. 3 показаны векторы плотности тока смещения и вид линий индукции их полей при зарядке конденсатора (а) – усиление электрического поля) и разрядке конденсатора ( б) – ослабление электрического поля).

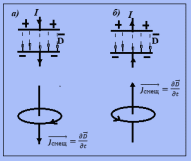
Рис. 3.

Как видно из представленных рис. 3, ток смещения, как и токи проводимости, является источником возникновения вихревого магнитного поля, то есть такого поля, циркуляция напряженности Н которого по замкнутому контуру не равна нулю.

Соответственно, при расчетах магнитных полей, в формулу закона полного тока:

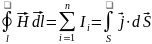
нужно подставлять полную плотность тока, складывающуюся из плотности тока проводимости и плотности тока смещения. Тогда, закон полного тока запишется так:

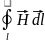= I_макро + 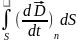, или, = .

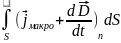Это есть второе основное уравнение Максвелл. Циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов проводимости и смещения, заключенных внутри данного контура, или – равна потоку плотности тока проводимости и плотности тока смещения сквозь поверхность, ограниченную этим контуром. Второе уравнение Максвелла устанавливает связь между токами проводимости и смещения и возникающим магнитным полем.

В общем случае токи проводимости и ток смещения не разделены в пространстве, как это было в конденсаторе с переменным напряжением на обкладках. Все типы токов существуют в одном и том же объеме и можно говорить о полном токе, равном сумме токов проводимости, конвекционных токов, а также токов смещения.

Если токи проводимости, конвекционные токи и все ЭДС кроме ЭДС магнитной индукции отсутствуют, то первое и второе уравнения Максвелла имеют симметричный вид:

=

и отличаются лишь знаками при производных в правых частях. Из сравнения двух уравнений можно сделать следующие выводы:

а) между электрическим и магнитным полями существует тесная взаимная связь. Изменение во времени электрического поля вызывает появление магнитного поля, а переменное магнитное поле является истоником вихревого электрического поля.

б) знаки при скоростях изменения потоков магнитной индукции и электрического смещения в обоих уравнениях различны, причем 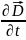и 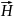образуют «правовинтовую» систему, а 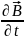и 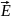- «левовинтовую».

Различия в знаках правых частей уравнений Максвелла соответствуют требованиям закона сохранения энергии и закона Ленца. В случае одинаковых знаков и даже малое увеличение одного из полей вызывало бы неограниченное возрастание обоих полей, а малое уменьшение одного из полей привело бы к полному исчезновению обоих. Различные знаки и являются необходимым условием устойчивого электромагнитного поля.

Рассмотрим третье уравнение, входящее в полную систему уравнений Максвелла.

Третье уравнение выражает теорему Остроградского –Гаусса для потока вектора электрического смещения:

.

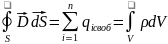Максвелл обобщил теорему Остроградского – Гаусса, предположив, что она справедлива не только для электростатических полей, но и для переменного электрического поля. Это уравнение показывает, что линии вектора электрического смещения могут начинаться и оканчиваться на зарядах.

Четвертое уравнение есть обобщение теоремы Остроградского – Гаусса для переменных магнитных полей:

.

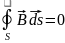Это уравнение отражает тот факт, что линии индукции магнитного поля 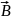замкнуты, и свободных магнитных «зарядов» в природе не существует.

Рассмотренные уравнения следует дополнить соотношениями, характеризующими электрические и магнитные свойства среды. Если среда изотропна, а все макротоки есть токи проводимости, то:

;

;

= .

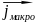Мы записали уравнения Максвелла в интегральной форме. Они связывают значения Е и Н вдоль некоторого контура со значениями D и B в точках поверхности, опирающейся на этот контур.

Согласно принципу относительности Эйнштейна, законы всех физических явлений, в том числе и электромагнитных, имеют одинаковый вид во всех инерциальных системах отсчета. Из принципа относительности вытекает, что раздельное рассмотрение электрического и магнитного полей весьма относительно.

Электромагнитные колебания

Свободные незатухающие колебания (идеальный колебательный контур).

Рассмотрим замкнутую электрическую цепь, состоящую из последовательно соединенных катушки индуктивности L, конденсатора емкости С и ключа К (рис.4). Пусть в начальный момент времени ключ разомкнут. Зарядим конденсатор, сообщив ему заряд q, а затем замкнем ключ. Конденсатор будет разряжаться, пойдет ток. Этот ток быстро прекратился бы, если бы не было катушки индуктивности L. Поскольку ток с течением времени начинает уменьшаться, возникнет ЭДС самоиндукции, которая поддержит ток. В результате конденсатор перезарядится и пойдет ток в обратном направлении. Такой вид колебаний называется свободным.

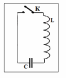
Рис. 4.

Если размеры электричесой цепи не слишком велики, а емкость конденсатора и индуктивность катушки не очень малы, то можно считать, что в каждый момент времени сила тока одинакова во всех сечениях этой цепи. Поэтому, мнгновенные значения силы переменного тока I должны удовлетворять всем законам для цепей постоянного тока.

Запишем для тока в контуре уравнение по второму правилу Кирхгофа: алгебраическая сумма напряжений на всех участках замкнутой цепи равна алгебраической сумме ЭДС. Поскольку мы пока не учитываем активное сопротивление цепи R, получаем:

U_c = 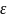_S , то есть напряжение на обкладках конденсатора равно ЭДС самоиндукции.

Но 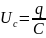, 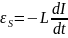. Отсюда:

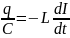
По определению, сила тока I= . Тогда предыдущее уравнение преобразуется к виду:

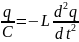или, 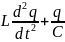= 0 , или 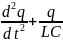= 0, или

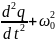q = 0, где .

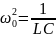Это уравнение есть однородное дифференциальное уравнение второго порядка. Его решение имеет вид:

q = q_m cos (ω₀t +φ) . То есть в контуре возникают свободные незатухающие колебания.

Здесь q_m – амплитуда колебаний заряда или максимальное значение заряда, ₀ - собственная (циклическая) частота, 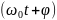- фаза колебаний в момент времени t,  - начальная фаза колебаний или фаза в момент времени t=0.

Сила тока в цепи при гармонических колебаниях.

Пусть колебание заряда происходит по закону 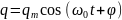. По определению, сила тока есть первая производная от заряда q по времени t. Тогда:

,

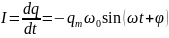а максимальное или амплитудное значение силы тока .

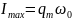Колебания силы тока сдвинуты по фазе относительно колебаний заряда на /2.

Таким образом, в колебательном контуре наблюдаются гармонические колебания заряда на обкладках конденсатора, напряжения на обкладках конденсатора 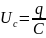и силы тока в цепи.

На рис. 5 представлены графики зависимости q, и I от времени. Для удобства изображения начальная фаза принята равной нулю =0, т.е. q = q_m при t =0.

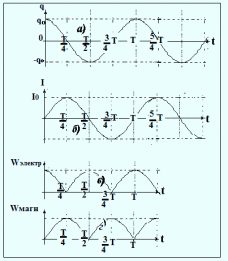
Рис. 5.

Энергия электрического и магнитного поля контура.

Переменный электрический ток в контуре вызывает появление переменного магнитного поля. Одновременно изменяется и электрическое поле. Поэтому рассмотренные нами свободные колебания заряда конденсатора и тока в контуре называются свободными электромагнитными колебаниями. В нашем рассмотренном случае, когда в начальный момент времени заряд на обкладках конденсатора равен максимальному значению, энергия этих колебаний в начальный момент времени равна электрической энергии зараженного конденатора (энергии электрического поля в конденсаторе), а затем эта энергия уменьшается и превращается в энергию магнитного поля катушки индуктивности L. Энергия магнитного поля определяется по формуле:

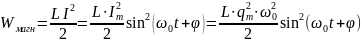
Энергия электрического поля равна:

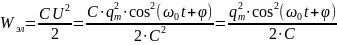
С учетом того, что = ,

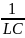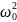полная энергия электромагнитного поля:

W = +

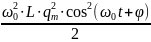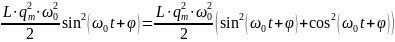
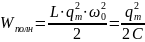
Видно, что полная энергия колебаний не зависит от времени. Следовательно, при гармонических ко­лебаниях выполняется закон сохранения энергии (идеальные колебания без рассеяния энергии). На рис. 5 представлены графики зависимости энергии электрического и магнитного полей от времени.

Отметим, что в реальном контуре всегда имеется рассеяние энергии в виде джоулевой теплоты, и колебания будут затухающими.