Случай размыкания цепи.

При t=0 величина ЭДС равна нулю ε=0, а сила тока I =I₀ = .

Отсюда:I = .

Сила тока уменьшается по экспоненте, а не сразу до нуля. График функции имеет вид, представленный на рис. 16.

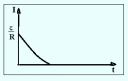
Рис. 16.

Токи Фуко.

Рассмотрим массивные проводники. При прохождении по проводникам переменного тока магнитное поле внутри проводника изменяется и там возникают вихревые токи самоиндукции, которые получили название токов Фуко.

В случае массивного круглого цилиндрического проводника плоскости токов самоиндукции проходят через ось.

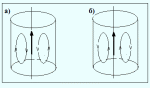
Рис. !7.

На рисунке а) рассмотрен случай, когда ток нарастает, а на рисунке б) – когда ток уменьшается. Эти токи противодействуют изменению тока внутри проводника и способствуют на поверхности. Следовательно, сопротивление внутри значительно больше, чем снаружи. Плотность тока максимальна на поверхности. Это явление наблюдается для токов высокой частоты и получило название скин – эффекта.

Количество теплоты, выделяемое в единицу времени вихревыми токами, прямо пропорционально квадрату частоты изменения магнитного поля (так как пропорционально силе тока в квадрате по закону Джоуля-Ленца). Поэтому, для выделения больших количеств теплоты, например, в индукционных печах, применяют токи высокой частоты.

С другой стороны, для уменьшения вредных потерь энергии, связанных с токами Фуко, магнитные цепи электрических машин и сердечники трансформаторов изготавливают из отдельных пластин, параллельных линиям магнитной индукции.

Взаимная индукция. Трансформатор.

Явление взаимной индукции заключается в наведении ЭДС индукции во всех проводниках, находящихся вблизи цепи переменного тока. Впервые это явление наблюдал Фарадей в опыте с двумя катушками (рис.18).

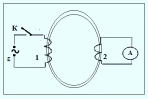
Рис. 18.

Из основного закона электромагнитной индукции следует:

ε₂ = - 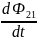, где ε₂ - ЭДС во втором контуре, а Ф₂₁ – магнитный поток сквозь поверхность второго контура, обусловленный магнитным полем тока, проходящим в первом контуре. Эту величину называют магнитным потоком взаимной индукции второго и первого контуров.

В соответствии с законом Био-Савара-Лапласа индукция магнитного поля первого контура пропорциональна току I. Тогда,

Ф₂₁ = L₂₁∙I₁ ,

где L₂₁ зависит от геометрической формы, размеров и взаимного расположения контуров, а также от относительной магнитной проницаемости среды, в которой контуры находятся. L₂₁ – взаимная индуктивность второго и первого контуров.

Если источник отключить от первого контура и подключить ко второму, то в последнем возникает ток I₂ . Магнитный поток сквозь поверхность первого контура будет Ф₁₂ = L₁₂∙I₂ .

Можно показать, что L₁₂ = L₂₁ Тогда ЭДС взаимной индукции определяется по формуле::

ε₂ = - .

Если L₂₁ = const, то ε₂ = - L₂₁ .

Если контуры 1 и 2 находятся в ферромагнитной среде, то L₂₁ зависит от силы тока I₁ . Тогда можно пользоваться аналогичной формулой: ε₂ = - L₂₁ , но здесь L_21динам - динамическая взаимная индуктивность второго и первого контуров.

На явлении взаимной индукции основано действие трансформаторов.

Рис. 19.

Трансформатор состоит из двух соленоидальных обмоток, укрепленных на общем замкнутом железном сердечнике.

Ф₂₁ = B₁∙S∙N₂ = , с другой стороны Ф₂₁ = L₂₁∙I₁ . Тогда: L₂₁ = .

Ясно, что L₂₁ = L₁₂ . По закону Кирхгофа для первого контура: ε₁ + ε_i = I₁∙R₁ → или ε₁ - L₁ = I₁∙R₁ .

Обычно I₁∙R₁ мало, тогда: ε₁ = L₁ .

Для второго контура, ε₂ = - L₂₁ . Но L₁ = , L₂₁ = . Отсюда,

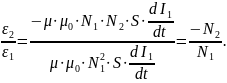
Изменения переменных ЭДС ε₂ и ε₁ происходят в противофазе.

Если считать мощности тока в первой и второй обмотках примерно одинаковыми, то:

ε₁ ∙ I₁ = ε₂ ∙I₂ и, соответственно,

- это есть коэффициент трансформации.

Энергия магнитного поля электрического тока соленоида:

Wмагн = .

Поскольку рассматриваемое поле соленоида является однородным и сосредоточено внутри соленоида, его энергия распределена равномерно по всему объему Vполя с объемной плотностью: ω _магн = .

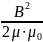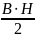Так как Н = , то, иначе, ω _магн = , где

ω _магн – объемная плотность энергии магнитного поля.

Рассмотрим неоднородное магнитное поле, создаваемое током I в контуре произвольной формы. Тогда: Wмагн = .

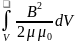С другой стороны, Wмагн= .

Отсюда следует: индуктивность контура численно равна удвоенной энергии магнитного поля, создаваемого проходящим по контуру током единичной силы.

Для случая, когда взаимодействуют несколько проводников, взаимная энергия токов:

Wвзаимн =