Электромагнитные волны.

В конце XIX века английский физик Джеймс Максвелл на основе своих уравнений создал единую тео­рию электромагнитных волн. Если возбудить с помощью зарядов переменное электрическое или магнитное поля, в окружающем пространстве возникает последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке в пространстве. Этот процесс будет периодическим во времени и пространстве и представляет собой волну. 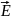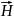Электромагнитная волна – это распростра­няющиеся в пространстве переменные электрическое и магнитное поля, которые ха­рактеризуются векторами напряженностей и электрического и магнитного полей. Согласно теории Максвелла, векторы 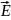и перпендику­лярны друг другу и направ­лению распро­странения волны, откуда следует, что электромагнит­ные волны по­перечны.

Если источник волны является точечным, то волна называется сферической. Если среда, в которой распространяется сферическая волна, однородная и изо­тропная (не содержит зарядов и токов ρ = 0, j =0), то векторы и удовлетворяют волновым уравне­ниям: 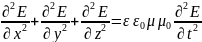и (1)

(2)

Всякая функция, удовлетворяющая уравнениям (1) и (2), описывает некоторую волну, причем фазовая скороять такой волны определяется по формуле: 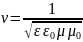(3)

Для вакуума: 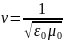. (4)

Плоская электромагнитная волна

Рассмотрим плоскую электромагнитную волну, распрстраняющуюся в однородной среде. Направим ось х перпендикулярно к волновым поверхностям для Е и Н.

Волновые уравнения в этом случае запишутся так:

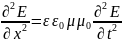
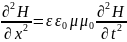
Решения этих уравнений плоской электромагнитной волны можно представить в виде:

Е = Е₀sin (ωt- kx+ φ); H = H₀sin (ωt- kx+ φ). (5)

Здесь Е₀ и Н₀ – амплитудные значения Е и Н, k = 2π/λ = ω/υ – волновое число, φ – начальная фаза колебания, х – рас­стояние, отсчитываемое вдоль направления распространения электромагнитной волны.

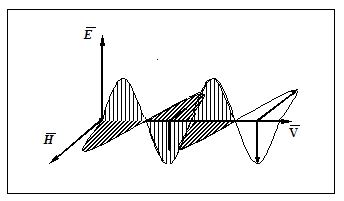
Рис. 1.

На рис.1 дана мгновенная фотография электромагнитной волны. Векторы и образуют с направлением распространения волны правовинтовую систему.

В фиксированной точке пространства векторы и изменяются со временем по гармоническому закону. Мгновенные значения Е и Н в любой точке про­странства связаны соотношением: 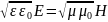, (6)

где ε₀ и μ₀ – электрическая и магнитная постоянные, ε и μ – ди­электрическая и магнитная проницаемости среды. Колебания векторов и происходят синфазно, т.е. они одновременно об­ращаются в ноль и одновременно достигают максимальных зна­чений.

_{Отсюда следует соотношение для амплитудных значений напряженности электрическо}й и магнитной составляющей волны: 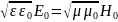(7)

Такие изменения векторов и происходят во всех точках пространства, но со сдвигом по фазе, определяемым расстоянием между точками.

Энергия электромагнитных волн

Фазовая скорость волны рассчитывается по формуле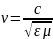 , где с – скорость света в вакууме. Сразу напомним, что в настоящее время считается, что это максимально достижимая скорость..

Электромагнитное поле обладает энергией, поэтому рас­пространение волн связано с переносом энергии в про­странстве. Энергия, переносимая волнами за единицу времени через единичную площадь поверхности, перпендикулярной скорости волны, называется плотностью потока энергии S электромаг­нитной волны или вектором Умова - Пойтинга. Численно плотность потока энергии равна произведению плотности энергии на скорость волны.

Плотность энергии электромагнитного поля: ω = ω_эл + ω_магн =

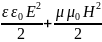
С учетом соотношения (6), получаем:

Или, с учетом выражения скорости волны: S = .

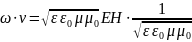Поскольку векторы и взаимно перпендикулярны, вектор Пойтинга можно записать так:

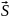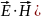= [ . (8)

Вектор совпадает по направлению с вектором скорости волны.

Среднее по времени значение плотности потока энергии S называют интенсивностью излучения I (I=<S>).

Шкала электромагнитных волн

В зависимости от длины волны электромагнитные волны принято делить на несколько видов.

1. Радиоволны: длинные (10⁵ – 10³) м, средние (10³- 10²) м, короткие (10² -10) м, ультра короткие (10 – 10^-3) м

2. Инфракрасные (10^-3 – 10^-6) м, видимая область (10^-6 – 10^-7), ультрафиолетовая область (10^-7 – 10^-9).

3. Рентгеновский диапазон (10^-9 – 10^-11 – 10^-13 ).

Вопросы для самопроверки

1) Дайте определение понятию электромагнитных волн. Какова скорость их распространения? Как можно графически изобразить электромагнитные волны?

2) Какой вид имеет уравнение электромагнитной волны?

3) Что такое шкала электромагнитных волн?

4) Каковы основные области применения электромагнитных волн?

5) Как связаны между собой скорость распространения волн, частота и длина волны?

6) Как связана скорость распространения волны в среде с диэлектрической и магнитной проницаемостью среды?

Пример 1.

Какова скорость электромагнитных волн в масле ?

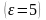Дано: 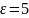, с = 3·10⁸м/с. Найти v.

Скорость волны определяется по формуле: ,

или с учетом формулы скорости в вакууме 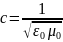, получаем: .

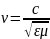У диамагнетиков и парамагнетиков µ ≈ 1, тогда 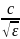v= ; и V= .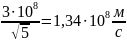

Ответ: V=

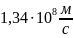
Пример 2.

Если увеличить в два раза объемную плотность энергии электромагнитной волны, то во сколько раз изменится плотность потока энергии волны?

Дано: ω₂ = 2ω₁; Найти: S₂ / S₁ ?

Рас­пространение световых волн связано с переносом энергии в про­странстве. Для ее характеристики был введен так называемый вектор плотности потока энергии S. Математически он равен произведению плотности энергии на скорость волны .

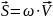Или S = v ∙ω, по условию задачи скорость волны v не меняется, следовательно: S₂ / S₁= ω₂/ ω₁ =2.

Ответ: S₂ / S₁=2.

Пример 3.

На полусферу радиуса r=30см, находящуюся в однородной среде с 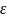=1 и µ =1, падает плоская монохроматическая электромагнитная волна, причем вершина полусферы обращена в сторону распространения волны. Амплитуда колебаний электрического вектора волны равна: Е₀ =200В/м (см.рис. 3) Определить энергию, падающую на полусферу за время t=1мин.

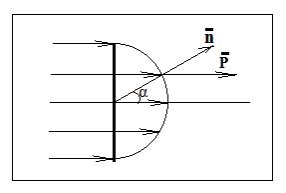
Рис. 2.

Дано: =1, µ =1, r = 30см = 0,3м, Е₀ =200В/м, t=1мин = 60с. Найти: W.

Для удобства решения задачи обозначим поток плотности энергии буквой Р. Тогда:

Мгновенный поток электрической энергии, падающей на элементарный участок полусферы dS, равен:

dФ = РdScosα,

где Р – численное значение вектора Умова-Пойтинга падающей волны на этой площадке, 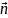– внешняя нормаль, восстановленная к ней, а угол α может меняться в пределах от 0 до π/2.

Ранее было показано, что P= E∙H∙sinβ, где β – угол между векторами и 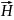. Векторы и всегда взаимно перпендикулярны, так что β всегда равен π/2. С учетом условия 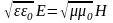_, для вектора Пойтинга получаем выражения:

P = 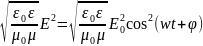и

dФ= .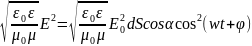

Энергия, падающая на площадку dS за время t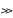 T, где Т – период колебаний волны, равна:

dW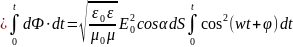

Проведем тригонометрическое преобразование: = , тогда:

dW=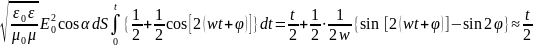 так как w= и если времяt T, то .

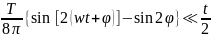Таким образом, dW=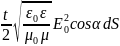 , где угол α меняется от 0 до π/2. Отсюда: W=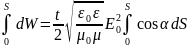

Согласно определению телесного угла, d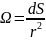 dS=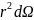

Вычисление интеграла можно заменить интегрированием по телесному углу, причем для полусферы (условие задачи) 0 ≤Ω ≤ 2π :

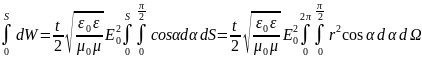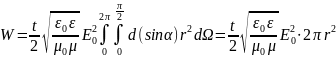W= ,

W=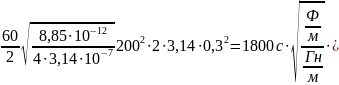

Ответ: W = 1800Дж.

Пример 4.

Передающая радиостанция работает на длине волны 30м. Сколько колебаний несущей частоты происходит в течение одного периода звуковых колебаний с частотой 5кГц?

Дано: λ₁=30м, с=3∙10⁸м/с, ν₂=5 ∙10³ Гц. Найти: N.

Для гармонической волны скорость волны, частота волны и длина волны связаны соотношением v=λ ∙ ν. По определению, период звуковых колебаний: Т₂=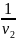 , а период радиоволны Т₁ = . Тогда число колебаний N= .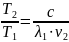

Отсюда, N = 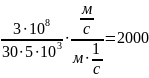. Ответ: N = 2000.