
лр 4
.docxМИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный химико-фармацевтический университет» Министерства здравоохранения Российской Федерации (ФГБОУ ВО СПХФУ Минздрава России)
Кафедра Процессов и аппаратов химической технологии
Отчет по практической работе №4
на тему
АНАЛИЗ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ САУ
по учебной дисциплине
Автоматизация процессов производства ГЛС
Семестр 7
Факультет химической технологии
Форма обучения - очная
по направлению подготовки (специальности): 18.03.01 Производство готовых лекарственных средств
уровень высшего образования – бакалавриат
Выполнил:
студентка IV
курса 570 группы Проявина Л.В. /![]() /
/
Проверил: Ганин П.Г. / ______________/
Проверил: Сорокин В.В. / ______________/
Санкт-Петербург,
2020 год
Цель работы:
Изучение критериев устойчивости линейных САР, исследование влияния величины коэффициента усиления разомкнутой системы на устойчивость линейной САР, а также использование программного приложения MathCad для анализа устойчивости САР.
Индивидуальное задание:
Вариант 3
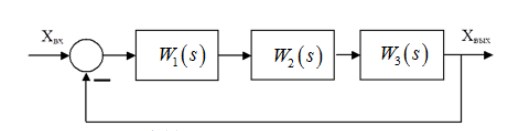
Рис. 1. Заданная структурная схема.
Ход работы:
1) По заданной структурной схеме (рисунок 1) составить передаточную функцию замкнутого контура, используя правила преобразования структурных схем.
Заданные передаточные функции звеньев:
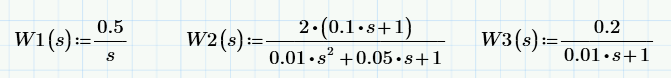
Для получения общей передаточной функции используем формулу для контура с отрицательной обратной связью:
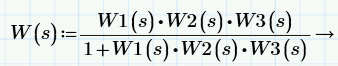
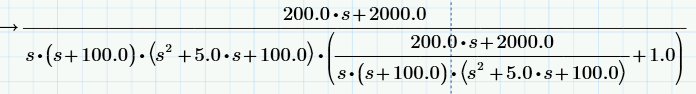
При вычислении передаточной функции замкнутого контура используем функцию «Collect», чтобы собрать элементы, содержащие переменную с одинаковым показателем степени.
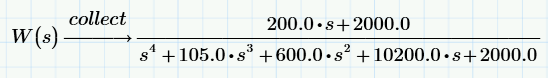
Характеристическим уравнением является знаменатель данной передаточной функции:
![]()
2) Проводим исследование устойчивости САУ тремя способами:
а) по корням характеристического уравнения.
Для нахождения корней характеристического уравнения (знаменателя) используем команду Solve – аналитическое решение уравнения.

Вывод: система устойчива, т.к. все вещественные части полученных корней отрицательны.
б) по критерию Гурвица.
Вводим характеристический полином:
![]()
Записываем коэффициенты характеристического уравнения:
![]()
Составляем определитель Гурвица и находим его значение:

Находим определители главных миноров:
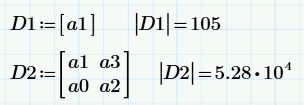
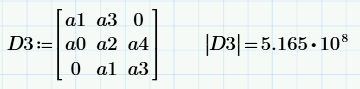
Вывод: система устойчива, т.к. все значения определителей больше нуля.
в) по критерию Михайлова.
Устойчивость САР по критерию Михайлова определяется по годографу характеристического полинома:
Присваиваем j значение мнимой единицы:
![]()
Если подставить в этот полином чисто мнимое значение s = j∙ω, то получим комплексный полином, называемый полиномом Михайлова. В характеристическом уравнении производим замену «s» на «j∙ω», используя функцию «substitute»:
![]()
Выделяем вещественную и мнимую части характеристического уравнения (вещественную и мнимую функции Михайлова), используя операторы Re и Im соответственно.
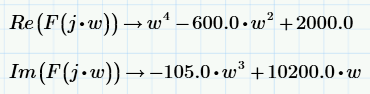
При изменении частоты ω вектор F(jω), изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости кривую, называемую кривой (годографом) Михайлова. Построим несколько годографов Михайлова, задавая разный интервал и шаг значений ω.
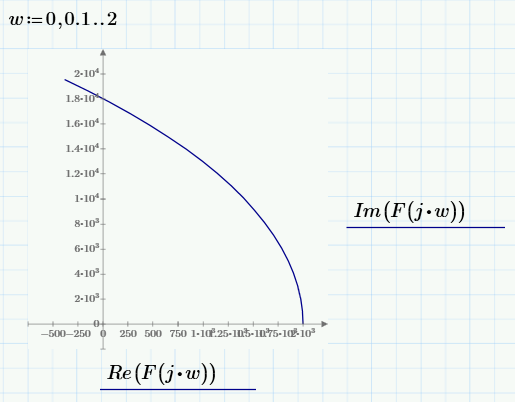

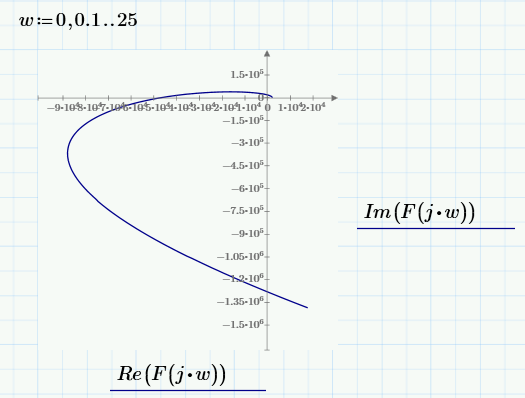
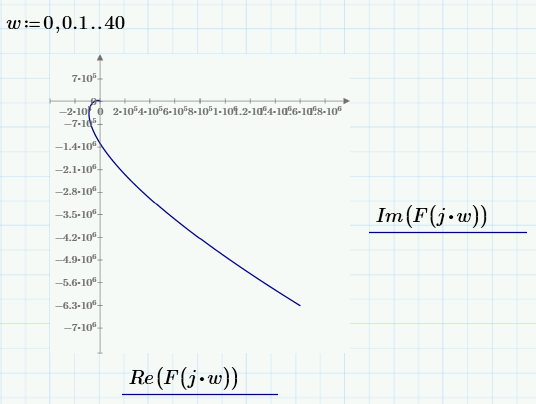
Годограф Михайлова уходит в бесконечность в 4 квадранте, т.к высшая степень в полиноме равна 4.
Вывод: корней, лежащих на мнимой оси и обращающих в нуль комплексный полином, нет; вектор кривой Михайлова F(jω) при изменении ω от 0 до +∞ повернулся, нигде не обращаясь в нуль, вокруг начала координат против часовой стрелки, следовательно, система устойчива.
Вывод по работе: в ходе лабораторной работы были изучены критерии устойчивости линейных САР, исследовано влияние величины коэффициента усиления разомкнутой системы на устойчивость линейной САР, а так же проанализирована устойчивость заданной САР с помощью MathCad.
