Лекции Муницына 2 курс / ПРИКЛАДНАЯ ФИЗИКА-2-7

ПРИКЛАДНАЯ ФИЗИКА

Лекция 7

Предыдущая лекция закончилась выводом уравнения осесимметричного изгиба круговой (кольцевой) пластины в перемещениях

Интегрирование дифференциального уравнения осесимметричного изгиба круговых пластин

Прежде всего, остановимся на другой записи уравнения (1)

В его справедливости можно убедиться, раскрыв скобки и проведя несложные операции дифференцирования

Напомним, что в цилиндрической системе координат оператор Лапласа имеет вид

а поскольку мы рассматриваем осесимметричное нагружение пластины

Таким образом, дифференциальное уравнение осесимметричного изгиба круговых пластин может быть записано в более коротком и красивом виде

∆∆ =

1

Вернемся к решению уравнения (1), и перепишем его в виде

Это неоднородное дифференциальное уравнение с переменными коэффициентами типа Эйлера. Из курса высшей математики мы помним, что его решение может быть получено с использованием замены переменных

=

Относительно новой переменной уравнение (3) принимает вид

Тех, кто захочет проверить это уравнение, должен предупредить, что переход от (3) к (4) довольно громоздкий. Решение уравнения (4) получается просто. Решение однородного уравнения приводит к характеристическому уравнению

4 − 43 + 42 = 0

его корни 1,2 = 0, 3,4 = 2. Им соответствует решение

0( ) = 1 + 2 + (3 + 4) 2

Для случая постоянной внешней нагрузки ( ) = 0 (равномерное давление) решение неоднородного уравнения

= 640 4

Переходя к переменной получаем решение уравнения (3), оно же (2), оно же (1)

Постоянные интегрирования 1 − 4 определяются из граничных условий, вид которых определяется способом закрепления краев (кромок) пластины.

2

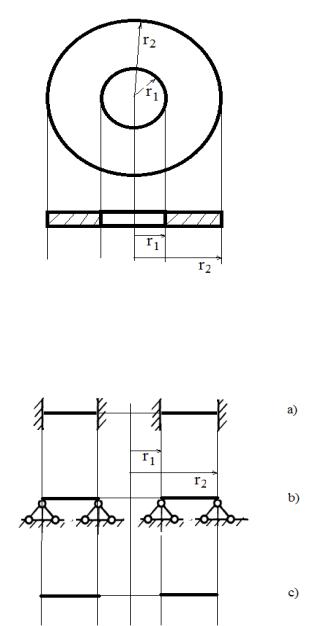
Типичные краевые условия

Укольцевой пластины есть две кромки – внутренняя = 1 и внешняя

= 2. На каждой из них можно записать по два граничных условия.

Рис. 7.1

Существует несколько типичных граничных условий (рис. 7.2).

Рис. 7.2

a) Жесткая заделка. Такая расчетная схема подойдет для расчета стальной кольцевой пластины прикрепленной с помощью сварки к жестким цилиндрическим поверхностям по внутренней и внешней кромкам. При таком закреплении на кромках = 1 и = 2 невозможен прогиб и поворот сечений. Граничные условия имеют вид

b) Шарнирная опора. Например, пластина опирается на две коаксиально расположенные тонкостенные цилиндрические оболочки. При этом некая внешняя нагрузка прижимает ее к цилиндрам. При таком закреплении на кромках = 1 и = 2 невозможен прогиб и равен нулю изгибающий момент . Граничные условия:

= 0, = 0 при = 1 и = 2

Эти же условия можно переписать, вспомнив формулу

с) Свободный край.

Мы перечислили не все возможные граничные условия, ниже мы обсудим и другие. Сейчас отметим следующее: выше рассмотрены случаи одинаковых условий закрепления на двух кромках пластины. Естественно, возможны их различные комбинации.

Например

Граничные условия

4

Граничные условия

Ну и так далее, сами можете посчитать число возможных комбинаций.

Cлучаями a,b,с, граничные условия не ограничиваются.

d) Нагруженный край пластины. На рисунке показана пластина, жестко закрепленная по внутренней кромке и нагруженная равномерно распределенными по внешнему контуру силой q и моментом m.

Чтобы подробнее объяснить, как получаются граничные условия при= 2, рассмотрим малый элемент пластины прилегающий к этой кромке

Это вид «сбоку» на элемент, который мы рисовали в предыдущей лекции при выводе уравнений равновесия. Обратите внимание, что здесь нарисованы положительные направления внутренних силовых факторов, . Из условия равновесия имеем

= , = при = 2

(Строго говоря, уравнения равновесия должны записываться аналогично уравнениям равновесия в предыдущей лекции. Туда входят слагаемые содержащие , но ими можно пренебречь.)

5

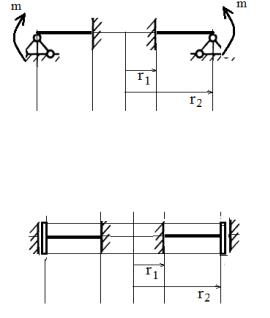
Если распределенная сила и момент направлены в противоположную сторону, они входят в граничные условия с противоположным знаком.

Вариант с) (свободный край) это частный случай d) для = 0, = 0.

При формулировке граничных условий всегда полезно задать себе вопрос: Что мне известно про четыре величины из следующей таблицы

(«+» означает что мы знаем эту величину, «− « - не знаем)

В каждой строчке число плюсов равно числу минусов равно двум.

В таблицу включены еще две строчки.

Нагруженный шарнир

И скользящая заделка

6

На схеме внешняя кромка жестко прикреплена к цилиндру, который может двигаться в вертикальном направлении по направляющим.

Частный случай 1. Круглая сплошная пластина

Рассмотрим круглую пластину, например, с жестким защемлением по внешней кромке.

пластины в начале координат конечен. Поэтому, из условия ограниченности решения, полагаем 3 = 0.

Здесь мы использовали правило Лопиталя. Полученный результат не противоречит здравому смыслу. Посмотрим, что происходит со второй производной, входящей в выражение изгибающих моментов , .

Следовательно, при наличии четвертого слагаемого в решении 4 2 ln моменты (а значит и эквивалентные напряжения) равны бесконечности при

→ 0. На этом основании также полагаем 4 = 0.

Врезультате имеем, что для круглой пластины решение имеет вид

Константы интегрирования определяются из двух граничных условий на внешней кромке пластины.

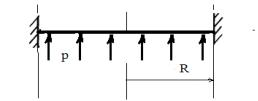
Частный случай 2. Пластина, нагруженная сосредоточенной силой, приложенной в центре

Рассмотрим расчетную схему

Сосредоточенная сила приложена в центре пластины. В точке приложения силы напряжения стремятся к бесконечности, но только потому, что сила приложена в точке. В действительности нагрузка распределяется по некоторой конечной площадке. В окрестности приложения силы гипотеза Кирхгофа-Лява не выполняется. Решение ищем в виде

К двум граничным условиям на кромке пластины добавляем условие равновесия элемента пластины в окрестности начала координат. Вырезаем круговой элемент радиуса .

Из условия равновесия

8

= 2

С другой стороны, поперечная сила может быть определена через погиб

Подставляя сюда (7.7) получаем

1= 44

Сравнивая эти два результата, получаем 4 = 8

Окончательно получаем

Не путать - сосредоточенную силу и – давление.

9