
Лекции в презентациях. 2 курс / Лекция Осесимметричный изгиб пластин
.pdf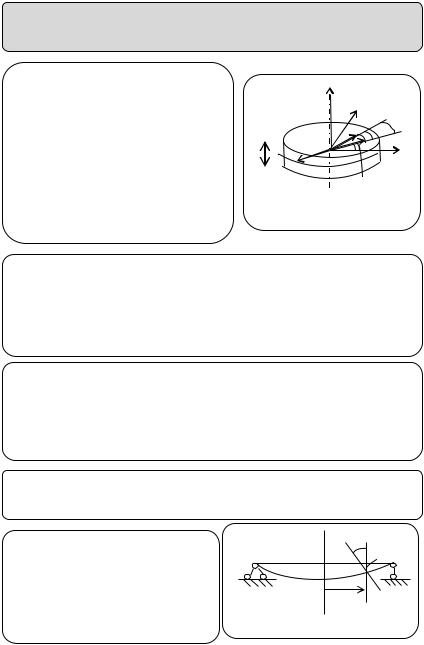
4.ОСЕСИММЕТРИЧНЫЙ ИЗГИБ КРУГОВЫХ ПЛАСТИН
Рассмотрим круговую пластину |
|
|
|
|
|
радиуса R, толщиной h, |
|
|
z |
y |
|
нагруженную силами |
|
|
|
|
|
|
|
|
|
dθ |
|
симметрично расположенными |
|
|
|
r |
|
|
|
|
|
||
относительно оси пластины Oz. |
h |
|
R |
|
|
Деформации, перемещения и |
|
|
|
x |
|
|
|
|
|
||
|
|
|
|
||
напряжения, возникающие в |
|
|
|
|
θ |
пластине, будут также |
|
|
|
|
|
симметричны относительно |
|
|
|
|
|
оси z. |
|
|
|
|
|
Расчет круговых и кольцевых пластин целесообразно проводить в полярной системе координат, связанной с декартовыми координатами соотношениями x = r cos , y = r sin , где r —
радиус рассматриваемой точки на срединной плоскости пластины, θ — полярный угол (окружная координата).
При расчете круговых пластин примем гипотезы, аналогичные принятым при расчете тонкостенных оболочек. Будем рассматривать пластины, у которых прогибы много меньше ее толщины (жесткие пластины) и в поперечных сечениях возникают только изгибающие моменты и поперечные силы.
Нормальные перемещения и относительные деформации в круговых пластинах.
|
φ |
|
Примем за нормальный прогиб |
w |
|
пластины w — перемещения |
||
|
||
точек срединной плоскости |
|
|
пластины, отсчитываемые от |
r |
|
|
||
горизонтальной плоскости |
|
|
вдоль оси z. |
|
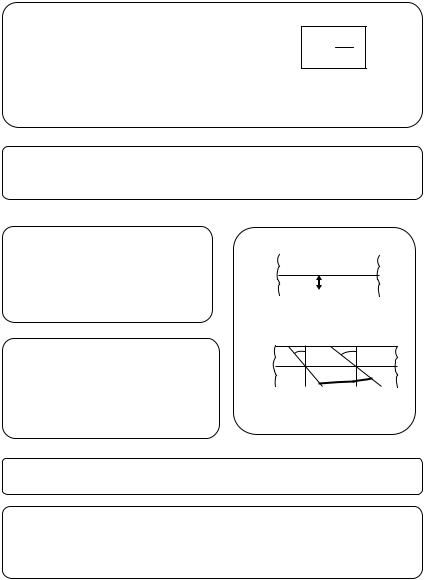
Угол поворота нормали к поверхности пластины φ связан с прогибом очевидным соотношением = − dwdr .
При отрицательном прогибе w 0 имеем положительный угол поворота нормали (угол поворота поперечного сечения пластины).
Относительная деформация в радиальном направлении.
Рассмотрим произвольное |
А1 |
|
А2 |
||
волокно CD, имеющее длину |
|
|
|
|
|
|
|
|
|
|
|
dz и отстоящее на расстоянии |
|
|
z |
|
|
z от срединной плоскости. |
C |
|
|
D |
|
|
|
|
|||
B1 |
|
B2 |
|||
|
|
||||
А |
|
А |
1 |
|
2 |
После деформации пластины |
φ |
φ+dφ |
нормаль А1В1 повернется на |
С |
D |
угол φ, нормаль А2В2 на угол |
|
|
В |
В |
|
(φ+dφ). Волокно CD |
1 |
2 |
|
|
|
удлинится. |
|
|
(CD) = (C D −CD)= z tg( + d ) − z tg z( + d ) − z zd
Относительная радиальная деформация
r = |
(CD) |
= |
zd |
= −z |
d 2w |
|
CD |
dz |
dr2 |
||||
|
|
|
Относительная деформация в окружном направлении.
Длина окружности, проходящая через точку С до изгиба пластины равна S0 = 2 r .
После изгиба пластины длина окружности |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
Sk |
= 2 (r + ztg ) 2 (r + z ) . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Относительная окружная деформация |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
= S = |
2 (r + z ) − 2 r |
|
= |
|
z |
|
= − |
z |
|
dw |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
S0 |
|
2 r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
r |
|
|
dr |
|
|
|
|
|
|
|||||||||||
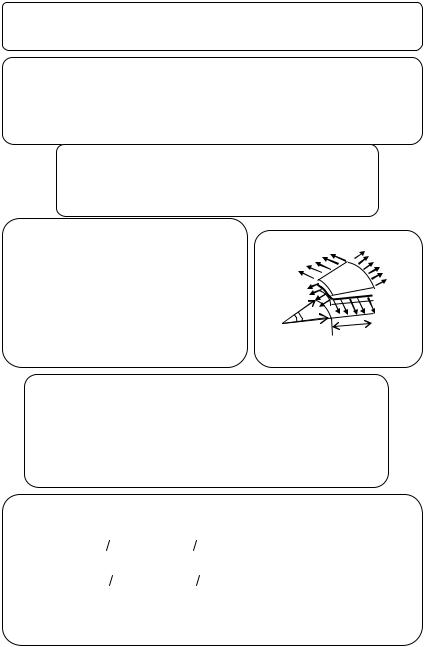
Радиальные и окружные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
напряжения в элементе круговой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|||||||||||||
пластины, вырезанном двумя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
осевыми сечениями под углом dθ и |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
двумя цилиндрическими |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
поверхностями радиусами r и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dθ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(r+dr) определяются согласно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
dr |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
закону Гука. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
r = |
|
|
E |
|
|
r + = − |
|
|
Ez |
|
|
|
|
d |
2w |
+ |
1 dw |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
(1 − |
) |
|
|
(1 − |
) dr |
|
|
|
|
|
|
r dr |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
E |
|
|
+ r = − |
|
Ez |
|
|
|
|
1 dw |
+ |
|
|
d 2w |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
− |
2 |
) |
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
dr |
2 |
|
|||||||||||||||||||||
(1 |
|
(1 |
|
|
) r dr |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Радиальный изгибающий момент — момент, действующий в радиальном направлении (погонный момент), Н•м/м
|
h 2 |
|
|
|
|
h 2 |
|
Ez |
|
|
d 2w |
|
1 dw |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
M r = − r |
z dz = + |
|
|
|
|
|
|
|
+ |
|
|
|
dz = |
||||||
(1 |
− |
2 |
) |
dr |
2 |
r dr |
|||||||||||||
|
−h 2 |
|
|
|
|
−h 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
d 2w |
|
|
1 dw |
|
|
|
|
|
|
|
|
|
|
|
|
||||
= D |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dr2 |
|
|
r dr |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Окружной изгибающий момент — момент, действующий в окружном направлении (погонный момент), Нм/м
h 2 |
h 2 |
|
Ez |
|
|
|
1 dw |
|
d 2w |
|||||
|
|
|
|
|
|
|||||||||
М = − z dz = + |
|
|
|
|
|
|
|
|
|
+ |
|
|
dz = |
|
(1 |
− |
2 |
) |
r dr |
dr |
2 |
||||||||
−h 2 |
−h 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=D 1 dw + d 2wr dr dr2
Здесь D = |
Eh3 |
12(1− 2 ) — цилиндрическая жесткость пластины. |
Уравнение равновесия элемента круговой пластины в усилиях.
Q — поперечные силы, |
|
|
|
|
|
|
|
|
|
|
|
||
возникающие на |
|
|
|
|
|
|
|
|
p |
||||
радиальных гранях, |
|
|
|
|
|
|
|
|
|
|
(Q+dQ) |
||
|
|
|
|
Q |
Mθ k |
||||||||
погонные силы — Н/м |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
(Mr+dMr) |
|||
pdr rd — внешняя |
|
|
|
|
Mr |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
сила от нормального |
|
|
|
|
r |
|
|
|
Mθ |
|
|||
|
|
|
|
|
|||||||||
давления p на |
|
|
|
|
dθ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
поверхности пластины |
|
|
|
|
r |
|
dr |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
Oz = 0 → pdr rd + Qrd − (Q + dQ)(r + dr)d = 0 |
|||||||||||||
|
dQ |
|
|
|
|
|
|
|
|
|
|
|
|
pr = r |
+ Q |
|
1 d |
|
|
|
|
|
|
|
|||
|
(Q r) = p |
|
|
||||||||||
|
dr |
|
|
|
|
|
|
||||||
|
|
r dr |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Уравнение моментов относительно правого края элемента
momk = 0 → M r rdr + (Q rd )dr − (M r + dMr )(r + dr)d + + 2M dr sin( d  2) + pdr rd dr
2) + pdr rd dr 2 = 0
2 = 0
dMr + (M r − M ) = p dr r
Уравнение равновесия в перемещениях, его решение.
После подстановки в последнее уравнение равновесия моментов их выражения через нормальный прогиб получим
|
d |
3w |
+ |
|
1 d |
|
2w |
|
− |
|
1 dw |
= Q |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
r |
|
|
dr2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
dr3 |
|
|
|
|
|
|
|
|
|
r 2 dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
d 2w |
|
|
|
|
1 dw |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
1 d |
dw |
|
|||||||||||||||||||||||||
|
|
|
+ |
|
= Q |
→→илиD |
|
= Q |
||||||||||||||||||||||||||||||||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
dr |
|
|
|
dr |
2 |
|
|
|
|
|
|
r dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
r dr |
dr |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
d ( w) |
|
|
= Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
d 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 d |
|
|
|
|
|
1 d |
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
где = |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
r |
|
|
|
— оператор Лапласа в |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
dr2 |
|
|
|
|
|
r dr |
|
|
|
r dr |
|
dr |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
полярной системе координат для осесимметричной деформации.
После подстановки последнего соотношения в 1-ое уравнение равновесия получим уравнение равновесия в перемещениях
D w = p

После четырехкратного интегрирования получим решение для
прогибов |
w(r) = C + C r2 |
+ C ln r + C r2 ln r + w , |
||
|
1 2 |
3 |
4 |
|
где w — частное решение. Для случая постоянного давления
= pr4
по поверхности пластины w 64D .
С1 ÷ С4 — постоянные интегрирования, определяемые из граничных условий на краях кольцевой пластины при r = r1 и
r = r2 . На каждом краю пластины формулируют по два краевых условия.
Жестко закрепленный край |
Шарнирно-опертый край |
|||||||||||||||||||||||||||
|
r |
|
w = 0 |
|
|
|
|
|
|
|
|
|
r |
w |
= 0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
= |
dw |
= 0 |
|
|
|
|
|
|
d 2 w |
|
dw |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
dr |
|
|
M |
r |
= D |
|
|
|
+ |
|
|
|
|
= 0 |
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
r dr |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Свободный край |
|
|
|
|
|
|
Нагруженный край |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m0 |
|
|
|
|
|
|
Mr = m0 |
|||||||
|
d 2 w |
|
|
dw |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
M r = D |
|
|
+ |
|
|
|
|
|
|
= 0 |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
dr |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
Qr = q |
|
|||||||
|
r |
|
|
|
d |
|
( w)= 0 |
|
q |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Q = D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
r |
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В результате дифференцирования решения для прогибов круговой пластины получим соотношения для углов поворота, изгибающих моментов и поперечной силы через постоянные интегрирования С1 ÷ С4.

= − |
dw |
= − |
|
2C2r + C3 |
1 |
+ C4r(1 + 2ln r) + |
|
|
pr3 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
dr |
|
|
r |
16D |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
d 2w |
|
|
|
|
1 dw |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 − ) |
|
|
||||||||||||||||||||
M r = D |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
= |
D |
2C2 |
(1 + ) − C3 |
|
|
|
|
|
+ |
|||||||||||||
|
|
|
|
2 |
|
|
|
|
r dr |
|
|
r |
2 |
||||||||||||||||||||||||||||
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ C4 ((3 + ) + 2(1 + ) ln r))+ |
|
pr2 |
(3 + ) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
16 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 dw |
|
|
|
|
|
d 2w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 − ) |
|
|
|||||||||||||||||
M = D |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
= D |
2C2 |
(1 + ) + C3 |
|
|
|
|
|
|
+ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
dr2 |
|
|
r |
2 |
|
||||||||||||||||||||||||||
r dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ C4 ((1 + 3 ) + 2(1 + ) ln r))+ |
|
pr2 |
(1 + 3 ) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
16 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3 |
w |
|
|
|
1 d |
2 |
|
w |
|
|
1 dw |
|
|
D |
|
|
|
|
pr |
|
|
||||||||||||||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Q = D |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
= 4C4 |
|
+ |
|
|
|
|
|
|||||||||||
dr |
3 |
|
r dr |
2 |
r |
2 |
|
dr |
r |
2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Всплошной пластине из условия ограниченности решений в центре при r = 0 полагаем С3 =С4=0. Тогда решение для
прогибов имеет вид
w(r) = C1 + C2r2 + w
