190 |
Chapter 4 Lexical and Syntax Analysis |
It is not difficult to see that together, these two rules generate the same language as the two rules with which we began. However, these two pass the pairwise disjointness test.
If the grammar is being used as the basis for a recursive-descent parser, an alternative to left factoring is available. With an EBNF extension, the problem disappears in a way that is very similar to the left factoring solution. Consider the original rules above for <variable>. The subscript can be made optional by placing it in square brackets, as in
<variable> → identifier [ [<expression] ]
In this rule, the outer brackets are metasymbols that indicate that what is inside is optional. The inner brackets are terminal symbols of the programming language being described. The point is that we replaced two rules with a single rule that generates the same language but passes the pairwise disjointness test.
A formal algorithm for left factoring can be found in Aho et al. (2006). Left factoring cannot solve all pairwise disjointness problems of grammars. In some cases, rules must be rewritten in other ways to eliminate the problem.
4.5 Bottom-Up Parsing
This section introduces the general process of bottom-up parsing and includes a description of the LR parsing algorithm.
4.5.1The Parsing Problem for Bottom-Up Parsers
Consider the following grammar for arithmetic expressions:
E → E + T | T
T → T * F | F
F → (E)| id
Notice that this grammar generates the same arithmetic expressions as the example in Section 4.4. The difference is that this grammar is left recursive, which is acceptable to bottom-up parsers. Also note that grammars for bottomup parsers normally do not include metasymbols such as those used to specify extensions to BNF. The following rightmost derivation illustrates this grammar:
E => E + T => E + T * F
=> E + T * id => E + F * id => E + id * id => T + id * id => F + id * id => id + id * id
4.5 Bottom-Up Parsing |
191 |
The underlined part of each sentential form in this derivation is the RHS that is rewritten as its corresponding LHS to get the previous sentential form. The process of bottom-up parsing produces the reverse of a rightmost derivation. So, in the example derivation, a bottom-up parser starts with the last sentential form (the input sentence) and produces the sequence of sentential forms from there until all that remains is the start symbol, which in this grammar is E. In each step, the task of the bottom-up parser is to find the specific RHS, the handle, in the sentential form that must be rewritten to get the next (previous) sentential form. As mentioned earlier, a right sentential form may include more than one RHS. For example, the right sentential form
E + T * id
includes three RHSs, E + T, T, and id. Only one of these is the handle. For example, if the RHS E + T were chosen to be rewritten in this sentential form, the resulting sentential form would be E * id, but E * id is not a legal right sentential form for the given grammar.
The handle of a right sentential form is unique. The task of a bottom-up parser is to find the handle of any given right sentential form that can be generated by its associated grammar. Formally, handle is defined as follows:
Definition: is the handle of the right sentential form = w if and only if S =7 *rm Aw =7 rm w
In this definition, =7 rm specifies a rightmost derivation step, and =7 *rm specifies zero or more rightmost derivation steps. Although the definition of a handle is mathematically concise, it provides little help in finding the handle of a given right sentential form. In the following, we provide the definitions of several substrings of sentential forms that are related to handles. The purpose of these is to provide some intuition about handles.
Definition: is a phrase of the right sentential form if and only if S =7 * = 1A 2 =7 + 1 2
In this definition, =>+ means one or more derivation steps.
Definition: is a simple phrase of the right sentential form if and only if S =7 * = 1A 2 =7 1 2
If these two definitions are compared carefully, it is clear that they differ only in the last derivation specification. The definition of phrase uses one or more steps, while the definition of simple phrase uses exactly one step.
The definitions of phrase and simple phrase may appear to have the same lack of practical value as that of a handle, but that is not true. Consider what a phrase is relative to a parse tree. It is the string of all of the leaves of the partial parse tree that is rooted at one particular internal node of the whole parse tree. A simple phrase is just a phrase that takes a single derivation step from its
192 |
Chapter 4 Lexical and Syntax Analysis |
root nonterminal node. In terms of a parse tree, a phrase can be derived from a single nonterminal in one or more tree levels, but a simple phrase can be derived in just a single tree level. Consider the parse tree shown in Figure 4.3.
Figure 4.3 |
E |
|
|
A parse tree for |
|
E + T * id |
T |
F
E |
+ |
T |
* |
id |
The leaves of the parse tree in Figure 4.3 comprise the sentential form E + T * id. Because there are three internal nodes, there are three phrases. Each internal node is the root of a subtree, whose leaves are a phrase. The root node of the whole parse tree, E, generates all of the resulting sentential form, E + T * id, which is a phrase. The internal node, T, generates the leaves T * id, which is another phrase. Finally, the internal node, F, generates id, which is also a phrase. So, the phrases of the sentential form E + T * id are E + T * id, T * id, and id. Notice that phrases are not necessarily RHSs in the underlying grammar.
The simple phrases are a subset of the phrases. In the previous example, the only simple phrase is id. A simple phrase is always an RHS in the grammar.
The reason for discussing phrases and simple phrases is this: The handle of any rightmost sentential form is its leftmost simple phrase. So now we have a highly intuitive way to find the handle of any right sentential form, assuming we have the grammar and can draw a parse tree. This approach to finding handles is of course not practical for a parser. (If you already have a parse tree, why do you need a parser?) Its only purpose is to provide the reader with some intuitive feel for what a handle is, relative to a parse tree, which is easier than trying to think about handles in terms of sentential forms.
We can now consider bottom-up parsing in terms of parse trees, although the purpose of a parser is to produce a parse tree. Given the parse tree for an entire sentence, you easily can find the handle, which is the first thing to rewrite in the sentence to get the previous sentential form. Then the handle can be pruned from the parse tree and the process repeated. Continuing to the root of the parse tree, the entire rightmost derivation can be constructed.
4.5.2Shift-Reduce Algorithms
Bottom-up parsers are often called shift-reduce algorithms, because shift and reduce are the two most common actions they specify. An integral part of every bottom-up parser is a stack. As with other parsers, the input to a
4.5 Bottom-Up Parsing |
193 |
bottom-up parser is the stream of tokens of a program and the output is a sequence of grammar rules. The shift action moves the next input token onto the parser’s stack. A reduce action replaces an RHS (the handle) on top of the parser’s stack by its corresponding LHS. Every parser for a programming language is a pushdown automaton (PDA), because a PDA is a recognizer for a context-free language. You need not be intimate with PDAs to understand how a bottom-up parser works, although it helps. A PDA is a very simple mathematical machine that scans strings of symbols from left to right. A PDA is so named because it uses a pushdown stack as its memory. PDAs can be used as recognizers for context-free languages. Given a string of symbols over the alphabet of a context-free language, a PDA that is designed for the purpose can determine whether the string is or is not a sentence in the language. In the process, the PDA can produce the information needed to construct a parse tree for the sentence.
With a PDA, the input string is examined, one symbol at a time, left to right. The input is treated very much as if it were stored in another stack, because the PDA never sees more than the leftmost symbol of the input.
Note that a recursive-descent parser is also a PDA. In that case, the stack is that of the run-time system, which records subprogram calls (among other things), which correspond to the nonterminals of the grammar.
4.5.3LR Parsers
Many different bottom-up parsing algorithms have been devised. Most of them are variations of a process called LR. LR parsers use a relatively small program and a parsing table that is built for a specific programming language. The original LR algorithm was designed by Donald Knuth (Knuth, 1965). This algorithm, which is sometimes called canonical LR, was not used in the years immediately following its publication because producing the required parsing table required large amounts of computer time and memory. Subsequently, several variations on the canonical LR table construction process were developed (DeRemer, 1971; DeRemer and Pennello, 1982). These are characterized by two properties: (1) They require far less computer resources to produce the required parsing table than the canonical LR algorithm, and (2) they work on smaller classes of grammars than the canonical LR algorithm.
There are three advantages to LR parsers:
1.They can be built for all programming languages.
2.They can detect syntax errors as soon as it is possible in a left-to-right scan.
3.The LR class of grammars is a proper superset of the class parsable by LL parsers (for example, many left recursive grammars are LR, but none are LL).
The only disadvantage of LR parsing is that it is difficult to produce by hand the parsing table for a given grammar for a complete programming language.
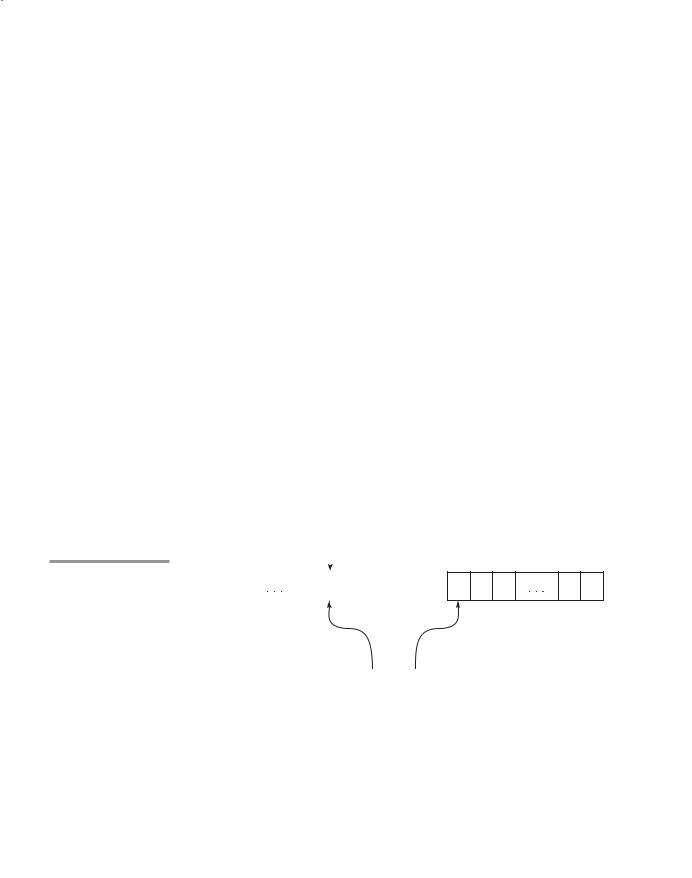
194 |
Chapter 4 Lexical and Syntax Analysis |
Figure 4.4
The structure of an LR parser
This is not a serious disadvantage, however, for there are several programs available that take a grammar as input and produce the parsing table, as discussed later in this section.
Prior to the appearance of the LR parsing algorithm, there were a number of parsing algorithms that found handles of right sentential forms by looking both to the left and to the right of the substring of the sentential form that was suspected of being the handle. Knuth’s insight was that one could effectively look to the left of the suspected handle all the way to the bottom of the parse stack to determine whether it was the handle. But all of the information in the parse stack that was relevant to the parsing process could be represented by a single state, which could be stored on the top of the stack. In other words, Knuth discovered that regardless of the length of the input string, the length of the sentential form, or the depth of the parse stack, there were only a relatively small number of different situations, as far as the parsing process is concerned. Each situation could be represented by a state and stored in the parse stack, one state symbol for each grammar symbol on the stack. At the top of the stack would always be a state symbol, which represented the relevant information from the entire history of the parse, up to the current time. We will use subscripted uppercase S’s to represent the parser states.
Figure 4.4 shows the structure of an LR parser. The contents of the parse stack for an LR parser have the following form:
S0X1S1X2 cXmSm (top)
where the S’s are state symbols and the X’s are grammar symbols. An LR parser configuration is a pair of strings (stack, input), with the detailed form
(S0X1S1X2S2 c XmSm, aiai + 1 c an$)
|
|
Parse Stack |
|
Top |
|
Input |
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
S0 |
X1 |
S1 |
|
Xm |
Sm |
|
ai ai+1 |
an $ |
|
|
|
|
|
|
|
|
|
|
|
Parser |
|
|
Parsing |
|
|
Code |
Table |
|
|
|
|
|
|
|
Notice that the input string has a dollar sign at its right end. This sign is put there during initialization of the parser. It is used for normal termination of the parser. Using this parser configuration, we can formally define the LR parser process, which is based on the parsing table.
4.5 Bottom-Up Parsing |
195 |
An LR parsing table has two parts, named ACTION and GOTO. The ACTION part of the table specifies most of what the parser does. It has state symbols as its row labels and the terminal symbols of the grammar as its column labels. Given a current parser state, which is represented by the state symbol on top of the parse stack, and the next symbol (token) of input, the parse table specifies what the parser should do. The two primary parser actions are shift and reduce. Either the parser shifts the next input symbol onto the parse stack or it already has the handle on top of the stack, which it reduces to the LHS of the rule whose RHS is the same as the handle. Two other actions are possible: accept, which means the parser has successfully completed the parse of the input, and error, which means the parser has detected a syntax error.
The rows of the GOTO part of the LR parsing table have state symbols as labels. This part of the table has nonterminals as column labels. The values in the GOTO part of the table indicate which state symbol should be pushed onto the parse stack after a reduction has been completed, which means the handle has been removed from the parse stack and the new nonterminal has been pushed onto the parse stack. The specific symbol is found at the row whose label is the state symbol on top of the parse stack after the handle and its associated state symbols have been removed. The column of the GOTO table that is used is the one with the label that is the LHS of the rule used in the reduction.
Consider the traditional grammar for arithmetic expressions that follows:
1.E → E + T
2.E → T
3.T → T * F
4.T → F
5.F → (E)
6.F → id
The rules of this grammar are numbered to provide a simple way to reference them in a parsing table.
Figure 4.5 shows the LR parsing table for this grammar. Abbreviations are used for the actions: R for reduce and S for shift. R4 means reduce using rule 4; S6 means shift the next symbol of input onto the stack and push state S6 onto the stack. Empty positions in the ACTION table indicate syntax errors. In a complete parser, these could have calls to error-handling routines.
LR parsing tables can easily be constructed using a software tool, such as yacc ( Johnson, 1975), which takes the grammar as input. Although LR parsing tables can be produced by hand, for a grammar of a real programming language, the task would be lengthy, tedious, and error prone. For real compilers, LR parsing tables are always generated with software tools.
The initial configuration of an LR parser is
(S0, a1 c an$)
196 |
Chapter 4 |
Figure 4.5
The LR parsing table for an arithmetic expression grammar
Lexical and Syntax Analysis |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Action |
|
|
|
|
|
Goto |
|
|
|
|
|
|
|
|
|
|
|
|
State |
id |
+ |
* |
( |
) |
$ |
|
E |
T |
F |
|
|
|
|
|
|
|
|
|
|
|
0 |
S5 |
|
|
S4 |
|
|
|
1 |
2 |
3 |
1 |
|
S6 |
|
|
|
accept |
|
|
|
|
2 |
|
R2 |
S7 |
|
R2 |
R2 |
|
|
|
|
3 |
|
R4 |
R4 |
|
R4 |
R4 |
|
|
|
|
4 |
S5 |
|
|
S4 |
|
|
|
8 |
2 |
3 |
5 |
|
R6 |
R6 |
|
R6 |
R6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
S5 |
|
|
S4 |
|
|
|
|
9 |
3 |
|
|
|
|
|
|
|
|
|
|
|
7 |
S5 |
|
|
S4 |
|
|
|
|
|
10 |
8 |
|
S6 |
|
|
S11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
R1 |
S7 |
|
R1 |
R1 |
|
|
|
|
10 |
|
R3 |
R3 |
|
R3 |
R3 |
|
|
|
|
11 |
|
R5 |
R5 |
|
R5 |
R5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The parser actions are informally defined as follows:
1.The Shift process is simple: The next symbol of input is pushed onto the stack, along with the state symbol that is part of the Shift specification in the ACTION table.
2.For a Reduce action, the handle must be removed from the stack. Because for every grammar symbol on the stack there is a state symbol, the number of symbols removed from the stack is twice the number of symbols in the handle. After removing the handle and its associated state symbols, the LHS of the rule is pushed onto the stack. Finally, the GOTO table is used, with the row label being the symbol that was exposed when the handle and its state symbols were removed from the stack, and the column label being the nonterminal that is the LHS of the rule used in the reduction.
3.When the action is Accept, the parse is complete and no errors were found.
4.When the action is Error, the parser calls an error-handling routine.
Although there are many parsing algorithms based on the LR concept, they differ only in the construction of the parsing table. All LR parsers use this same parsing algorithm.
Perhaps the best way to become familiar with the LR parsing process is through an example. Initially, the parse stack has the single symbol 0, which