14.4 Задача о наилучшем использовании ресурсов

При решении задач данного типа необходимо определить оптимальный вариант выпуска продукции или выполнения работ при определенном количестве имеющихся ресурсов, с получением максимального дохода.

Допустим, что предприятие имеет в своём распоряжении определённое количество ресурсов: рабочую силу, деньги, сырьё, оборудование, производственные площади и т.п. При этом предприятие может выпускать продукцию четырёх видов или оказывать четыре вида услуг. Информация о количестве единиц каждого ресурса, необходимых для производства одного вида продукции (услуг), и доходах, получаемых предприятием от единицы каждого вида товаров, либо заранее известна.

Пример

Предприятие изготавливает четыре вида продукции. Для производства продукции используются ресурсы – трудовые, материальные, финансовые. Максимальный запас ресурсов на производстве 16, 110, 100 соответственно. Расход ресурсов на единицу производства продукции и предельно допустимые значения выпуска каждого вида даны в таблице.

Требуется определить, в каком количестве надо выпустить продукцию четырех типов: Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурсов каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице 14.1.

Таблица 14.1 – Нормы расхода и прибыль

Ресурс	Прод1	Прод2	Прод3	Прод4	Наличие
Прибыль	60	70	120	130
Трудовые	1	1	1	1	16
Сырье	6	5	4	3	110
Финансы	4	6	10	13	100

Составим математическую модель, для чего введем следующие обозначения:

x_j – количество выпускаемой продукции j- типа, j=1..4;

b_i – количество распределяемого ресурса - го вида, i =1..3;

a_ij – норма расхода i-го ресурса для выпуска единицы продукции j-го типа;

c_j – прибыль, получаемая от реализации единицы продукции j- го типа.

Математическая модель.

Ограничения:

x₁+x₂+x₃+x₄  16

6x₁+5x₂+4x₃+3x₄  110

4x₁+6x₂+10x₃+13x₄  100

x_j  0; j=1..4

где х₁,х₂,х₃,х₄ – количество выпускаемой Прод1, Прод2, Прод3, Прод4.

Целевая функция – это прибыль от реализации продукции, которая составит:

F=60x₁+70x₂+120x₃+130x₄ max

То есть среди всех неотрицательных решений системы линейных неравенств требуется найти такое, при котором функция F принимает максимальное значение.

Создадим на листе Excel таблицу для ввода данных как показано на рисунке 14.2.

Рисунок 14.2 – Ввод исходных данных

Блок ячеек С4:F4 содержит оптимальное решение, значение этих ячеек будет получено в результате решения задачи.

Блок ячеек С3:F3 содержит значения прибыли от реализации продукции. В ячейках C8: F10 отображен расход ресурсов на единицу производства продукции каждого вида.

Для вычисления целевой функции в ячейке G4 используем функцию =СУММПРОИЗВ(С3:F3; С4:F4) (рисунок 14.3).

Рисунок 14.3 – Ввод целевой функции

В ячейки G8:F10 введены формулы для расчета ограничений по ресурсам с использованием функции =СУММПРОИЗВ($С$4:$F$4; С8:F8). На рисунке 14.4 представлена таблица с исходными данными, целевой функцией, ограничениями и граничными условиями.

Рисунок 14.4 – Ввод ограничений

На вкладке Данные в группе Анализ выберем команду Поиск решения.

На экране отобразится ДО Параметры поиска решения, в котором установим следующие параметры (рисунок 14.5):

 в поле Оптимизировать целевую функцию указываем адрес ячейки со значением целевой функции – G4;

 переключатель До устанавливаем на максимум целевой функции;

 в поле Изменяя ячейки переменных указываем адреса ячеек со значениями искомых переменных B4:F4;

 в области В соответствии с ограничениями с помощью кнопки Добавить размещаем все ограничения задачи;

 установим флажок в поле Сделать переменные без ограничений неотрицательными;

 в списке Выберите метод решения указываем Поиск решения линейных задач симплекс-методом;

 нажимаем кнопку Найти решение.

Рисунок 14.5 – Заполнение ДО Поиск решения

Все ограничения указаны в системе при составлении математической модели задачи. Для добавления ограничения необходимо выбрать кнопку Добавить. Отобразится ДО Добавление ограничений.

В поле Ссылка на ячейки указываем адрес диапазона G8:G10, выбираем в раскрывающемся списке знак неравенства ≤, в поле Ограничение выделяем диапазон H8:H10 и нажимаем кнопку Добавить (рисунок 14.6). Результатом этого действия будет добавление текущего ограничения в список ограничений, поля окна Добавление ограничения будут очищены для ввода следующего ограничения. Вводим ограничения на неотрицательные целые значения объема выпуска продукции.

Порядок ввода ограничений не имеет значения. Главное – не забыть ни одно из ограничений. Для принятия последнего ограничения и возврата к диалоговому окну Параметры поиска решения нажмем кнопку OK.

Рисунок 14.6 – Добавление ограничений

Результат выполнения Поиска решений представлен на рисунке 14.7.

Рисунок 14.7 – Результаты Поиска решения

Таким образом, максимальная прибыль при реализации продукции будет получена в размере 1320 у. е. при следующем плане производства:

10 – объем продукции типа 1;

0 – объем продукции типа 2;

6 – объем продукции типа 3;

0– объем продукции типа 4;

Кроме поиска оптимальных значений в изменяемые ячейки, Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их названия в ДО Результаты поиска решения (рисунок 14.8). Для выбора нескольких отчетов из списка использовать клавишу Shift.

Рисунок 14.8 – Сохранение результатов Поиска решений

Отчет по результатам (рисунок 14.9) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления и окончательное значение, во второй – значения искомых переменных: исходные и полученные в результате решения задачи, в третьей – результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как состояние и допуск. Состояние принимает значение «Привязка», если вводимые ограничения совпадают с ограничениями, полученными в результате вычислений, и значение «Без привязки» в противном случае.

По значениям столбца Допуск можно сделать вывод о недоиспользованных ресурсах. В рассматриваемой задаче трудовые ресурсы и финансы были использованы полностью (значение в столбце Допуск равно 0), сырье использовано не полностью (недоиспользованными оказались 26 единиц).

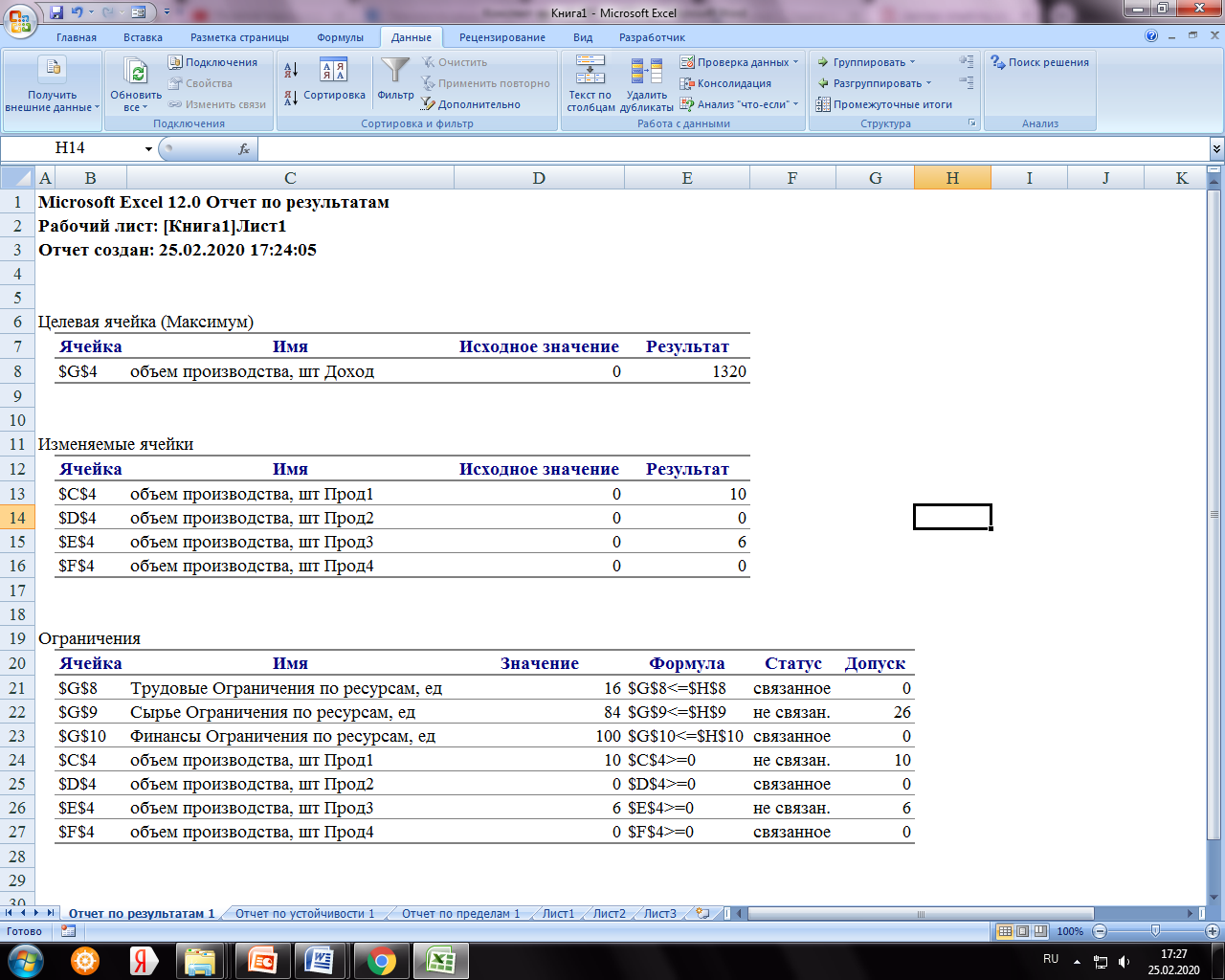
Рисунок 14.9 – Отчет по результатам

Отчет по устойчивости (рисунок 14.10) содержит два блока: Ячейки переменных и Ограничения. Первый блок содержит информацию по допустимому увеличению и уменьшению коэффициентов целевой функции при условии, что объем оптимальной продукции не изменится. Второй блок касается увеличения и уменьшения значений ограничений.

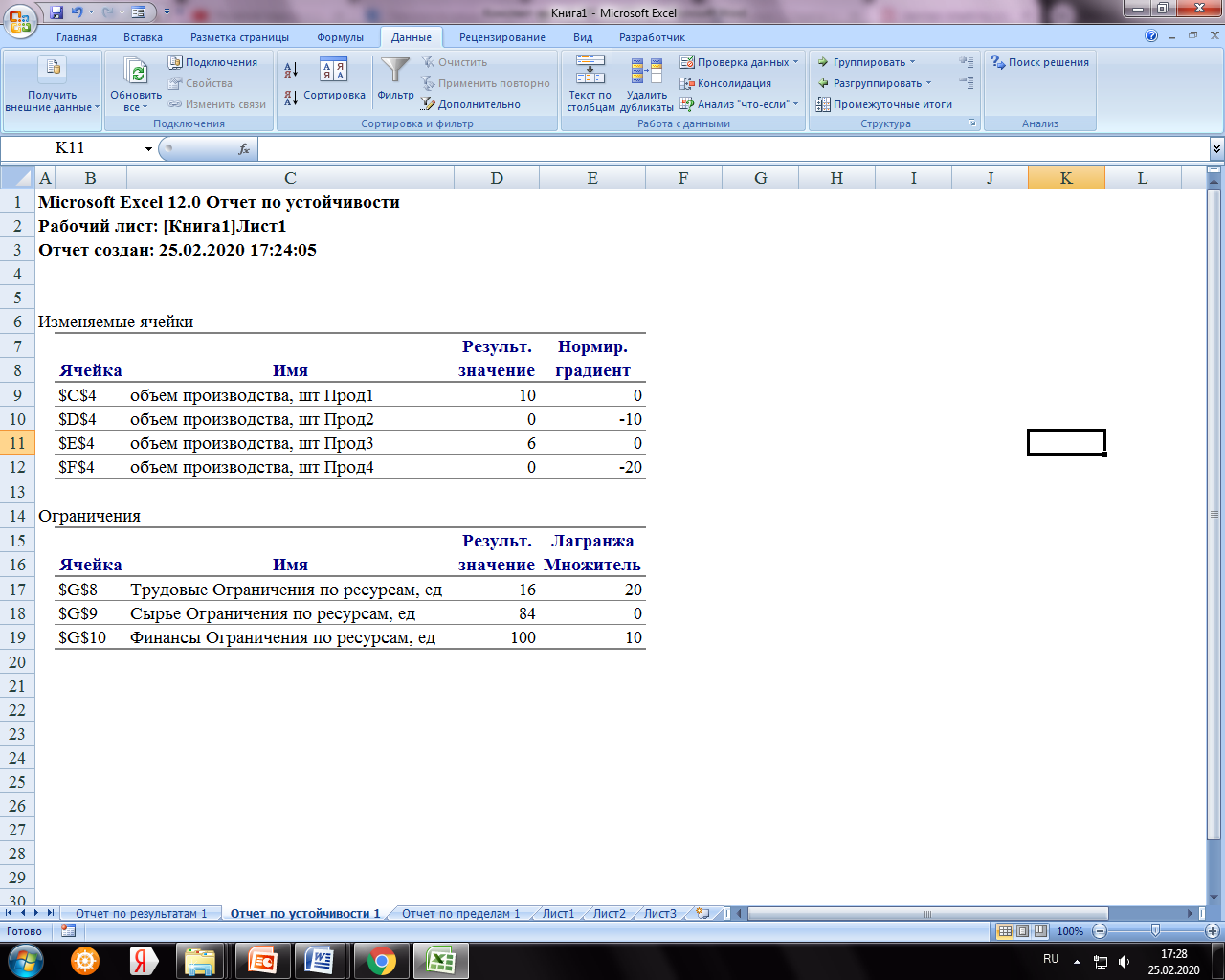
Рисунок 14.10 – Отчет по устойчивости

Отчет по пределам (рисунок 14.11) содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.

Рисунок 14.11 – Отчет по пределам