МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова» (БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова»)
	БГТУ.СМК-Ф-4.2-К5-01
Факультет			Е		Оружие и системы вооружения
			шифр		наименование
Кафедра			Е7		Механика деформируемого твердого тела
			шифр		наименование
Дисциплина			Сопротивление материалов

КУРСОВАЯ РАБОТА

на тему

Расчет статически неопределимых рам.

Влияние изменения температуры на реакции опор.

Выполнил студент группы
Фамилия И.О.				Подпись
РУКОВОДИТЕЛЬ
Фамилия И.О. Подпись
Оценка
«_____»						20__г.

САНКТ-ПЕТЕРБУРГ

2021

Содержание

Введение 3

Метод сил 4

Канонические уравнения метода сил 6

Решение статически неопределимых рам без учета воздействия температур 8

Канонические уравнения метода сил с учетом температуры 10

Решение статически неопределимых рам с учетом воздействия температур 11

Заключение 13

Список литературы 14

Введение

Данная курсовая работа выполнена по дисциплине «сопротивление материалов» - науке об инженерных методах расчета на прочность, жесткость и устойчивость простейших элементов конструкции. Рассмотрим каждое из понятий определения.

Прочность – способность тела сохранять размеры и форму в пространстве, не разрушаясь.

Жесткость – способность тела сопротивляться нагрузкам, сохраняя форму и размеры.

Устойчивость – способность тела сохранять форму, размеры, положение в пространстве центра тяжести под нагрузкой.

Статически неопределенная система – система, в которой количество неизвестных реакций или внутренних усилий превышает полезное количество уравнений статики.

Целью работы является решение задач со статически неопределимой системой с учетом температуры и без и выявление зависимости значений реакций опоры от данного показателя.

Задачи, способствующие выполнению цели:

• Раскрытие статически неопределимости системы;

• Решение эквивалентной статически определимой системы;

• Построение эпюр продольных и поперечных сил, изгибающих моментов;

• Проверка решения через расчет горизонтального перемещения одной из опор (если необходимо).

Метод сил

Самым распространенным методом раскрытия статической неопределимости системы (балки или рамы) является метод сил.  Его суть заключается в следующем: в неопределимой системе все дополнительные внешние и внутренние связи заменяются силами и моментами. Их величина в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями.

Система, освобождённая от дополнительных связей, становится статически определимой, и носит название основной системы. Существует несколько способов удаления связей, которые и определяют вид основной системы:

• Полное удаление некоторых опор или их замена опорами с меньшим числом связей;

• Постановка шарниров в промежуточных сечениях стержней. Это позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту, являющемуся лишней неизвестной.

• Рассечение стержня, устраняющее три связи, которые соответствуют внутренним усилиям M, Q, N.

Алгоритм расчета системы методом сил:

1. Определение степени статической неопределимости;

2. Выбор основной системы;

3. Составление статически определимой эквивалентной системы (ЭСОС);

4. Запись системы канонических уравнений;

5. Составление грузовой системы, нагруженной только известными нагрузками, и единичных систем, количество которых определяется из статической неопределимости (количество неизвестных сил равно количеству систем), построение эпюр;

6. Вычисление коэффициентов при неизвестных и свободных членов системы канонических уравнений;

7. Решение системы канонических уравнений, то есть определение значений неизвестных реакций опор;

8. Построение окончательные эпюры для данной системы.

Канонические уравнения метода сил

Для эквивалентной системы составляют канонические уравнения, число которых равно степени статической неопределенности.

,

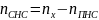где 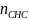- число уравнений системы, 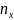– число неизвестных сил, 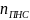- число полезных уравнений.

В эквивалентной системе перемещения по направлению отброшенных связей должны равняться нулю. На основании принципа независимости действия сил перемещения по i-тому направлению от всех сил можно представить в виде:

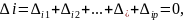(1)

Здесь первые индексы означают направления перемещения (и одновременно направление отбрасываемой связи), а вторые — причину, вызвавшую эти перемещения. Таким образом 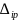 — означает перемещение по направлению i от k-го силового фактора. Обозначим через 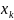реакцию связи k, тогда поскольку перемещение пропорционально соответствующей силе, то

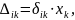(2)

где 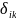 - единичное перемещение по - тому направлению от силы .

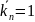Подставляя (2) в (1), получим:

(3)

Таким образом, условие эквивалентности основной и заданной «n» статически неопределимой системы сводится к системе «n» линейных алгебраических уравнений:

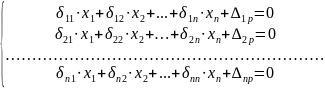(4)

Уравнения (4) являются каноническими уравнениями метода сил. Они позволяют раскрыть статические нагрузки системы. Первое из (4) означает, что перемещения по первому направлению от всех сил равно нулю и т.д.

Для расчета коэффициентов при неизвестных используются интегралы Мора:

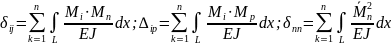
где 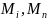- моменты от единичных сил, приложенных по направлениям i и n; 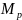– момент, вызванный системой внешних сил.

Решение статически неопределимых рам без учета воздействия температур

Канонические уравнения метода сил с учетом температуры

Изменение температурного режима статически неопределимых систем, как правило, приводит к появлению в них внутренних усилий и напряжений. Лишь в некоторых случаях напряженное состояние системы не меняется с изменением температуры. Одним из примеров может служить статически неопределимая рама.

В связи с тем, что рама в отношении своих опорных закреплений статически определима, она при одинаковом равномерном нагреве или охлаждении всех ее элементов свободно деформируется, приобретая форму, подобную начальной.

Канонические уравнения метода сил при расчете любой статически неопределимой системы на действие температуры имеют вид:

Где 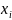— любая приложенная к балке сила, — имеют те же значения, что и при расчете на действие внешней нагрузки; 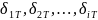  - представляют собой температурные перемещения в основной системе по направлениям лишних неизвестных усилий. Их можно вычислить с помощью интеграла 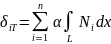, где 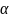– температурный коэффициент.

Решение статически неопределимых рам с учетом воздействия температур

Заключение

Рассмотрев два решения задачи (с учетом и без учета температуры) и сравнивая полученные значения, можно сделать следующие выводы: под влиянием температуры сила реакции опоры возрастает в ≈6 раз, а момент практически не изменяется. Данную зависимость можно определить только по корням уравнений системы, так как визуально эпюры продольных N_i, поперечных Q_i сил и крутящих моментов M_z изменяются незначительно.

Это говорит о том, что данное изменение температур недостаточно для возникновения критических сечений.

Список литературы

1. Решение задач начального уровня по сопротивлению материалов: практическое пособие / Н.Г. Буткарева [и др.]; под. ред. В.А. Санникова; Балт. гос. техн. ун-т. – СПб., 2015. – 90 с. ISBN 978-5-85546-892-2;

2. Решение задач средней сложности по сопротивлению материалов: практическое пособие / Н.Г.Буткарева [и др.]; под. ред. В.А.Санникова; Балт. гос. техн. ун-т. – СПб., 2016. – 78 с. ISBN 978-5-85546-961-5